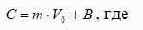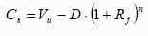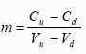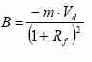следует понять, какое влияние могут оказать те или иные решения на результат проекта, т.е. построить такое же дерево для проекта уже с учётом влияния опционов. И наконец, рассчитав эффект проекта с учётом опционов, отнять от него базисный эффект без их учёта. Так можно получить ценность самого реального опциона. Можно пойти по другому пути. После того, как будет построено базисное дерево решений, второе дерево можно строить уже для самого опциона. Для этого в узлах дерева надо оценить эффект, получаемый непосредственно от самого опциона, а не от комбинации «проект + опцион». Результат расчёта по такому дереву даст эффект опциона (а не проекта с опционом). В любом случае вычисление стоимости опциона данным методом представляет собой движение по «дереву решений», где в каждой точке менеджеры стараются принять наилучшие решения. В итоге денежные потоки, возникающие как следствие будущих решений, сводятся к приведенной стоимости. Однако в реальной жизни «дерево решений», как правило, имеет гораздо больше узлов принятия решений. Но чем больше узлов принятия решений, тем сложнее сделать оценку. После моделирования движения цены рассматриваемого актива формируется репликативный портфель. Целью его создания является использование комбинации безрискового актива и рассматриваемого актива для моделирования движения цены опциона. В данном случае применяются правила арбитража, и стоимость репликативного портфеля должна быть равна стоимости опциона. В общем случае стоимость опциона будет определяться разностью произведения текущей стоимости базового актива и коэффициента «дельта» и суммы дополнительного финансирования для покупки базового актива, источником которой является короткая продажа безрискового актива. Коэффициент «дельта» можно рассчитать следующим образом:
В случае многопериодного биномиального процесса оценка опциона
происходит итеративно. Она начинается с последнего периода и движется к
началу дерева. На каждом временном отрезке создаются репликационные
портфели для получения стоимости опциона в данном периоде. В результате
получаем стоимость опциона в текущий момент.
На практике основные трудности при использовании биномиальной
модели связаны с определением значений относительного роста или
снижения стоимости бизнеса в каждом периоде, а также вероятностей
положительного и негативного варианта развития событий. Для расчёта этих
параметров разработаны соответствующие формулы.
Итак, возможный рост стоимости бизнеса можно рассчитать следующим
образом:
u=es, где
�� u – относительный рост (u=1,25 =>ожидается рост стоимости проекта в 25%).
�� s – стандартное отклонение среднегодовой стоимости проекта.
�� h – интервал как часть года (h=0,5 => решение по проекту принимается 1 раз в полгода).
Относительное снижение стоимости (d) рассчитывается по формуле:
d=1/u. 
Вероятность относительного роста (П), исходя из предположений о
нейтральном отношении к риску, можно рассчитать как:
П = [(1+r)-d]/u-d/
Соответственно вероятность снижения стоимости проекта будет равна
1-П.
Модель Кокса-Росса-Рубинштейна. (метод репликативного портфеля).1
Используя этот метод, мы заменяем опцион на активы компании на
эквивалентный ему синтетический опцион, представляющий собой покупку
этих активов на заемные деньги. При этом мы предполагаем, что поскольку
оба опциона (синтетический и реальный) полностью эквивалентны по своему
действию, они должны иметь одинаковую ценность для инвестора.
Другими словами, опцион мы заменяем инвестиционным портфелем,
ценность которого равна премии по опциону:
�� C - премия по CALL-опциону (ценность 100% акций предприятия).
�� 0 V - ценность базисного актива (активов предприятия) сегодня.
�� m - параметр, отражающий долю базисного актива в
репликативном портфеле, имеющем свойства оцениваемого опциона.
�� B - сумма долга в репликативном портфеле (отрицательное число).
Максимальный выигрыш при реализации опциона через n лет будет равен:
Параметр m вычисляется по следующей формуле:
Зная параметр m , можно найти сумму долга в репликативном портфеле:
А затем вычислить С по вышеприведённой формуле. 
