Как уже говорилось, при анализе больших систем наполнителем каналов связи между элементами, подсистемами и системы в целом могут быть:
· продукция, т. е. реальные, физически ощутимые предметы с заранее заданным способом их количественного и качественного описания;
· деньги, с единственным способом описания — суммой;
· информация, в виде сообщений о событиях в системе и значениях описывающих ее поведение величин.
Начнем с того, что обратим внимание на тесную (системную!) связь показателей продукции и денег с информацией об этих показателях. Если рассматривать некоторую физическую величину, скажем — количество проданных за день образцов продукции, то сведения об этой величине после продажи могут быть получены без проблем и достаточно точно или достоверно. Но, уже должно быть ясно, что при системном анализе нас куда больше интересует будущее — а сколько этой продукции будет продано за день? Этот вопрос совсем не праздный — наша цель управлять, а по образному выражению “управлять — значит предвидеть”.
Итак, без предварительной информации, знаний о количественных показателях в системе нам не обойтись. Величины, которые могут принимать различные значения в зависимости от внешних по отношению к ним условий, принято называть случайными (стохастичными по природе). Так, например: пол встреченного нами человека может быть женским или мужским (дискретная случайная величина); его рост также может быть различным, но это уже непрерывная случайная величина — с тем или иным количеством возможных значений (в зависимости от единицы измерения).
Для случайных величин (далее — СВ) приходится использовать особые, статистические методы их описания. В зависимости от типа самой СВ — дискретная или непрерывная это делается по разному.
Дискретное описание заключается в том, что указываются все возможные значения данной величины (например - 7 цветов обычного спектра) и для каждой из них указывается вероятность или частота наблюдений именного этого значения при бесконечно большом числе всех наблюдений.

Можно доказать (и это давно сделано), что при увеличении числа наблюдений в определенных условиях за значениями некоторой дискретной величины частота повторений данного значения будет все больше приближаться к некоторому фиксированному значению — которое и есть вероятность этого значения.
К понятию вероятности значения дискретной СВ можно подойти и иным путем — через случайные события. Это наиболее простое понятие в теории вероятностей и математической статистике — событие с вероятностью 0.5 или 50% в 50 случаях из 100 может произойти или не произойти, если же его вероятность более 0.5 - оно чаще происходит, чем не происходит. События с вероятностью 1называют достоверными, а с вероятностью 0 — невозможными.
Отсюда простое правило: для случайного события X вероятности P(X) (событие происходит) и P(X) (событие не происходит), в сумме для простого события дают 1.
Если мы наблюдаем за сложным событием — например, выпадением чисел 1..6 на верхней грани игральной кости, то можно считать, что такое событие имеет множество исходов и для каждого из них вероятность составляет 1/6 при симметрии кости.
Если же кость несимметрична, то вероятности отдельных чисел будут разными, но сумма их равна 1.
Стоит только рассматривать итог бросания кости как дискретную случайную величину и мы придем к понятию распределения вероятностей такой величины.

xmlns:o="urn:schemas-microsoft-com:office:office" xmlns:dt="uuid:C2F41010-65B3-11d1-A29F-00AA00C14882" xmlns="http://www.w3.org/TR/REC-html40">

Случайные события и величины, их основные характеристики 2

Пусть в результате достаточно большого числа наблюдений за игрой с помощью одной и той же кости мы получили следующие данные:

Таблица 2.1

Грани	1	2	3	4	5	6	Итого
Наблюдения	140	80	200	400	100	80	1000

Подобную таблицу наблюдений за СВ часто называют выборочным распределением, а соответствующую ей картинку (диаграмму) — гистограммой.

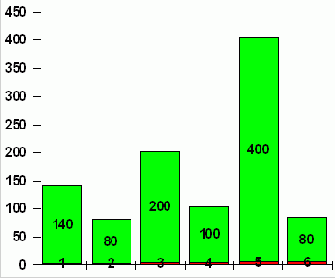
Рис. 2.1

Какую же информацию несет такая табличка или соответствующая ей гистограмма?

Прежде всего, всю — так как иногда и таких данных о значениях случайной величины нет и их приходится либо добывать (эксперимент, моделирование), либо считать исходы такого сложного события равновероятными — по на любой из исходов.

С другой стороны — очень мало, особенно в цифровом, численном описании СВ. Как, например, ответить на вопрос: — а сколько в среднем мы выигрываем за одно бросание кости, если выигрыш соответствует выпавшему числу на грани?

Нетрудно сосчитать:

1•0.140+2•0.080+3•0.200+4•0.400+5•0.100+6•0.080= 3.48

То, что мы вычислили, называется средним значением случайной величины, если нас интересует прошлое.

Если же мы поставим вопрос иначе — оценить по этим данным наш будущий выигрыш, то ответ 3.48 принято называть математическим ожиданием случайной величины, которое в общем случае определяется как

Mx = å Xi · P(Xi); {2 - 1}

где P(Xi) — вероятность того, что X примет свое i-е очередное значение.

Содержание Вперед

Таким образом, математическое ожидание случайной величины (как дискретной, так и непрерывной)— это то, к чему стремится ее среднее значение при достаточно большом числе наблюдений.
Обращаясь к нашему примеру, можно заметить, что кость несимметрична, в противном случае вероятности составляли бы по 1/6 каждая, а среднее и математическое ожидание составило бы 3.5.
Поэтому уместен следующий вопрос - а какова степень асимметрии кости - как ее оценить по итогам наблюдений?
Для этой цели используется специальная величина — мера рассеяния — так же как мы "усредняли" допустимые значения СВ, можно усреднить ее отклонения от среднего. Но так как разности (Xi - Mx) всегда будут компенсировать друг друга, то приходится усреднять не отклонения от среднего, а квадраты этих отклонений. Величину

{2 - 2}
принято называть дисперсией случайной величины X.
Вычисление дисперсии намного упрощается, если воспользоваться выражением

т. е. вычислять дисперсию случайной величины через усредненную разность квадратов ее значений и квадрат ее среднего значения.
Выполним такое вычисление для случайной величины с распределением рис. 1.

Таким образом, дисперсия составит 14.04 - (3.48)2 = 1.930.
Заметим, что размерность дисперсии не совпадает с размерностью самой СВ и это не позволяет оценить величину разброса. Поэтому чаще всего вместо дисперсии используется квадратный корень из ее значения — т. н. среднеквадратичное отклонение или отклонение от среднего значения:

составляющее в нашем случае

Сообразим, что в случае наблюдения только одного из возможных значений (разброса нет) среднее было бы равно именно этому значению, а дисперсия составила бы 0. И наоборот - если бы все значения наблюдались одинаково часто (были бы равновероятными), то среднее значение составило бы

(1+2+3+4+5+6) / 6 = 3.500;
усредненный квадрат отклонения — (1 + 4 + 9 + 16 + 25 + 36) / 6 =15.167;
а дисперсия 15.167-12.25 = 2.917.
Ядро JavaScript 1.5. СправочникСодержание раздела