d9e5a92d

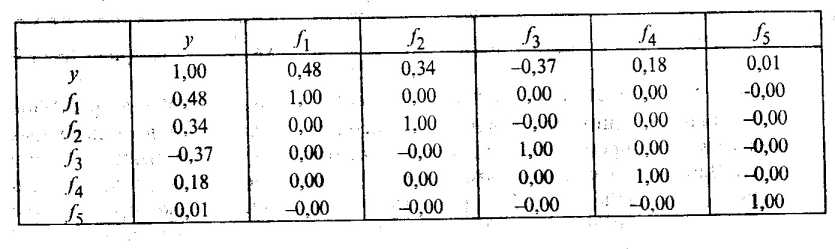
Матрица парных коэффициентов корреляции

Из матрицы факторных нагрузок А следует, что первая главная компонента наиболее тесно связана со следующими показателями: x1 число колесных тракторов на 100 га (a11 = rx1f1 = 0,95); х2 число зерноуборочных комбайнов на 100 га (rx2f1 = 0,97); х3 число орудий поверхностной обработки почвы на 100 га (rx3f1 = 0,94). В этой связи первая главная компонента f1 интерпретирована как уровень механизации работ.
Вторая главная компонента f2 тесно связана с количеством удобрений (х4) и химических средств оздоровления растений (x5), расходуемых на гектар, и интерпретирована как уровень химизации растениеводства.
Уравнение регрессии на главных компонентах строится по данным вектора значений результативного признака Y и матрицы F значений главных компонент.
Некоррелированность главных компонент между собой и тесноту их связи с результативным признаком у показывает матрица парных коэффициентов корреляции (табл. 53.3).
Анализ матрицы парных коэффициентов корреляции свидетельствует о том, что результативный признак у наиболее тесно связан с первой (ryf1 = 0,48), третьей (ryf3 = 0,37) и. второй (ryf2 = 0,34) главными компонентами. Можно предположить, что только эти главные компоненты войдут в регрессионную модель у. Таблица 53.3
Первоначально в модель у включают все главные компоненты (в скобках указаны расчетные значения t-критерия):
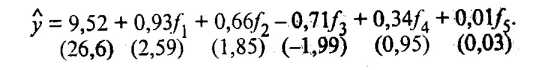(53.41)
Качество модели характеризуют: множественный коэффициент детерминации r = 0,517, средняя относительная ошибка аппроксимации = 10,4%, остаточная дисперсия s2 = 1,79 и Fнабл = 121. Ввиду того что Fнабл Fкр =2,85 при = 0,05, v1 = 6, v2 = 14, уравнение регрессии значимо и хотя бы один из коэффициентов регрессии 1, 2, 3, 4 не равен нулю. Если значимость уравнения регрессии (гипотеза Н0: 1 = 2 = 3 = 4 = 0 проверялась при = 0,05, то значимость коэффициентов регрессии, т.е. гипотезы H0: j = 0 (j = 1, 2, 3, 4), следует проверять при уровне значимости, большем, чем 0,05, например при = 0,1. Тогда при = 0,1, v = 14 величина tкр = 1,76, и значимыми, как следует из уравнения (53.41), являются коэффициенты регрессии 1, 2, 3.
Учитывая, что главные компоненты не коррелированы между собой, можно сразу исключить из уравнения все незначимые коэффициенты, и уравнение примет вид 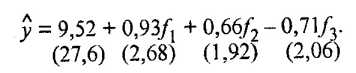(53.42)
Сравнив уравнения (53.41) и (53.42), видим, что исключение незначимых главных компонент f4 и f5, не отразилось на значениях коэффициентов уравнения b0 = 9,52, b1 = 0,93, b2 = 0,66 и соответствующих tj (j = 0, 1, 2, 3). Это обусловлено некоррелированностью главных компонент. Здесь интересна параллель уравнений регрессии по исходным показателям (53.22), (53.23) и главным компонентам (53.41), (53.42).
Уравнение (53.42) значимо, поскольку Fнабл = 194 Fкр = 3,01, найденного при = 0,05, v1 = 4, v2 = 16. Значимы и коэффициенты уравненPя, так как tj tкр. = 1,746, соответствующего = 0,01, v = 16 для j = 0, 1, 2, 3. Коэффициент детерминации r = 0,486 свидетельствует о том, что 48,6% вариации у обусловлено влиянием трех первых главных компонент.
Уравнение (53.42) характеризуется средней относительной ошибкой аппроксимации = 9,99% и остаточной дисперсией s2 = 1,91.
Уравнение регрессии на главных компонентах (53.42) обладает несколько лучшими аппроксимирующими свойствами по сравнению с регрессионной моделью (53.23) по исходным показателям: r = 0,486 r = 0,469; = 9,99% (х) = 10,5% и s2(f) = 1,91 s2(x) = 1,97. Кроме того, в уравнении (53.42) главные компоненты являются линейными функциями всех исходных показателей, в то время как в уравнение (53.23) входят только две переменные (x1 и х4).

В ряде случаев приходится учитывать, что модель (53.42) трудноинтерпретируема, так как в нее входит третья главная компонента f3, которая нами не интерпретирована и вклад которой в суммарную дисперсию исходных показателей (x1, ..., х5) составляет всего 8,6%.

Однако исключение f3 из уравнения (53.42) значительно ухудшает аппроксимирующие свойства модели: r = 0,349; = 12,4% и s2(f) = 2,41. Тогда в качестве регрессионной модели урожайности целесообразно выбрать уравнение (53.23). 53.4. Кластерный анализ
В статистических исследованиях группировка первичных данных является основным приемом решения задачи классификации, а поэтому и основой всей дальнейшей работы с собранной информацией. Традиционно эта задача решается следующим образом. Из множества признаков, описывающих объект, отбирается один, наиболее информативный, с точки зрения исследователя, и производится группировка данных в соответствии со значениями этого признака.

Если требуется провести классификацию по нескольким признакам, ранжированным между собой по степени важности, то сначала осуществляется классификация по первому признаку, затем каждый из полученных классов разбивается на подклассы по второму признаку и т.д.

Подобным образом строится большинство комбинационных статистических группировок.
В тех случаях, когда не представляется возможным упорядочить классификационные признаки, применяется наиболее простой метод многомерной группировки создание интегрального показателя (индекса), функционально зависящего от исходных признаков, с последующей классификацией по этому показателю.
Развитием этого подхода является вариант классификации по нескольким обобщающим показателям (главным компонентам), полученным с помощью методов факторного или компонентного анализа.
При наличии нескольких признаков (исходных или обобщенных) задача классификации может быть решена методами кластерного анализа, которые отличаются от других методов многомерной классификации отсутствием бучающих выборок, т.е. априорной информации о распределении генеральной совокупности.
Различия между схемами решения задачи по классификации во многом определяются тем, что понимают под понятиями сходство и степень сходства.
После того как сформулирована цель работы, естественно попытаться определить критерии качества, целевую функцию, значения которой позволят сопоставить различные схемы классификации.
В экономических исследованиях целевая функция, как правило, должна минимизировать некоторый параметр, определенный на множестве объектов (например, целью классификации оборудования может явиться группировка, минимизирующая совокупность затрат времени и средств на ремонтные работы).
В случаях когда формализовать цель задачи не удается, критерием качества классификации может служить возможность содержательной интерпретации найденных групп.
Рассмотрим следующую задачу. Пусть исследуется совокупность п объектов, каждый из которых характеризуется k измеренными признаками.

Требуется разбить эту совокупность на однородные в некотором смысле группы (классы). При этом практически отсутствует априорная информация о характере распределения k-мерного вектора Х внутри классов.
Полученные в результате разбиения группы обычно называются кластерами* (таксонами**, образами), методы их нахождения кластер-анализом (соответственно численной таксономией или распознаванием образов с самообучением).
* Clаster (англ.) группа элементов, характеризуемых каким-либо общим свойством.
**Тахоп (англ.) систематизированная группа любой категории. Необходимо с самого начала четко представлять, какая из двух задач классификации подлежит решению. Если решается обычная задача типизации, то совокупность наблюдений разбивают на сравнительно небольшое число областей группирования (например, интервальный вариационный ряд в случае одномерных наблюдений) так, чтобы элементы одной такой области находились друг от друга по возможности на небольшом расстоянии. Решение другой задачи заключается в определении естественного расслоения результатов наблюдений на четко выраженные кластеры, лежащие друг от друга на некотором расстоянии.
Если первая задача типизации всегда имеет решение, то во втором случае может оказаться, что множество наблюдений не обнаруживает естественного расслоения на кластеры, т.е. образует один кластер.
Хотя многие методы кластерного анализа довольно элементарны, основная часть работ, в которых они были предложены, относится к последнему десятилетию. Это объясняется тем, что эффективное решение задач поиска кластеров, требующее выполнения большого числа арифметических и логических операций, стало возможным только с возникновением и развитием вычислительной техники.
Обычной формой представления исходных данных в задачах кластерного анализа служит матрица
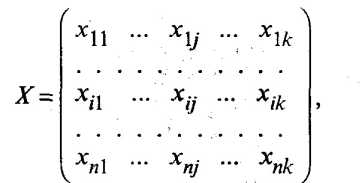
каждая строка которой представляет результаты измерений k рассматриваемых признаков у одного из обследованных объектов. В конкретных ситуациях может представлять интерес как группировка объектов, так и группировка признаков.

В тех случаях, когда разница между двумя этими задачами не существенна, например при описании некоторых алгоритмов, мы будем пользоваться только термином объект, включая в это понятие и термин признак. Матрица Х не является единственным способом представления данных в задачах кластерного анализа. Иногда исходная информация задана в виде квадратной матрицы
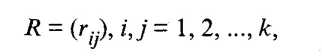
элемент rij которой определяет степень близости i-го объекта к j-му. Большинство алгоритмов кластерного анализа полностью исходит из матрицы расстояний (или близостей) либо требует вычисления отдельных ее элементов, поэтому если данные представлены в форме X, то первым этапом решения задачи поиска кластеров будет выбор способа вычисления расстояний, или близости, между объектами или признаками.
Несколько проще решается вопрос об определении близости между признаками. Как правило, кластерный анализ признаков преследует те же цели, что и факторный анализ: выделение групп связанных между собой признаков, отражающих определенную сторону изучаемых объектов.

Мерой близости в этом случае служат различные статистические коэффициенты связи. Расстояние между объектами (кластерами) и мера близости
Наиболее трудным и наименее формализованным в задаче классификации является определение понятия однородности объектов. В общем случае понятие однородности объектов задается введением либо правила вычисления расстояний (xi, хj) между любой парой исследуемых объектов (x1, x2, ...,xn), либо некоторой функцией r(хi, xj), характеризующей степень близости i-го и j-го объектов.
Если задана функция (xi, хj), то близкие с точки зрения этой метрики объекты считаются однородными, принадлежащими к одному классу. Очевидно, что необходимо при этом сопоставлять (xi, хj) с некоторыми пороговыми значениями, определяемыми в каждом конкретном случае по-своему.


Аналогично используется и мера близости r(xi, хj), при задании которой мы должны помнить о необходимости выполнения следующих условий: симметрии r(xi, хj) = r(xj, хi); максимального сходства объекта с самим собой r(xi, хi) = r(xi, хj), 1 i, j п, и монотонного убывания r(xi, хj) по мере увеличения (xi, хj), т.е. из (xk, хl) (xi, хj) должно следовать неравенство r(xk, хl) (xi, хj).
Выбор метрики, или меры близости, является узловым моментом исследования, от которого в значительной степени зависит окончательный вариант разбиения объектов на классы при данном алгоритме разбиения. В каждом конкретном случае этот выбор должен производиться по-своему, в зависимости от целей исследования, физической и статистической природы наблюдений, априорных сведений о характере вероятностного распределения X.
Рассмотрим наиболее широко используемые в задачах кластерного анализа расстояния и меры близости.
Обычное евклидово расстояние определяется по формуле 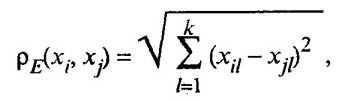(53.43)
где xil, хjl значения l-го признака у i-го (j-го) объекта (l = 1, 2, ..., k, i,j = 1, 2, .... п). Оно используется в следующих случаях:
а) наблюдения берутся из генеральной совокупности, имеющей многомерное нормальное распределение с ковариационной матрицей вида 2Ek, где Еk единичная матрица, т.е. исходные признаки взаимно независимы и имеют одну и ту же дисперсию;
б) исходные признаки однородны по физическому смыслу и одинаково важны для классификации.
Естественное с геометрической точки зрения евклидово пространство может оказаться бессмысленным (с точки зрения содержательной интерпретации), если признаки измерены в разных единицах. Чтобы исправить положение, прибегают к нормированию каждого признака путем деления центрированной величины на среднее квадратическое отклонение и переходят от матрицы Х к нормированной матрице с элементами
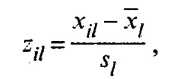
где xil значение l-го признака у i-го объекта; среднее значение l-го признака;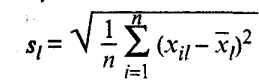
среднее квадратическое отклонение l-го признака.
Однако эта операция может привести к нежелательным последствиям. Если кластеры хорошо разделимы по одному признаку и не разделимы по другому, то после нормирования дискриминирующие возможности первого признака будут уменьшены в связи с усилением шумового эффекта второго.
Взвешенное евклидово расстояние определяется из выражения 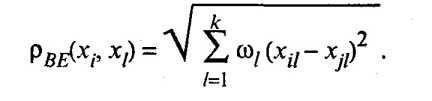(53.44)
Оно применяется в тех случаях, когда каждой l-й компоненте вектора наблюдений Х удается приписать некоторый вес 1, пропорциональный степени важности признака в задаче классификации. Обычно принимают 0 l 1, где l = 1,2, ..., k. Определение весов, как правило, связано с дополнительными исследованиями, например с организацией опроса экспертов и обработкой их мнений. Определение есов l только по данным выборки может привести к ложным выводам.
Хеммингово расстояние используется как мера различия объектов, задаваемых дихотомическими признаками. Это расстояние определяется по формуле 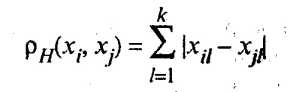(53.45)
и равно числу несовпадений значений соответствующих признаков в рассматриваемых i-м и j-м объектах. Как правило, решение задач классификации многомерных данных предусматривает в качестве предварительного этапа исследования реализацию методов, позволяющих выбрать из k исходных признаков x1, x2, ..., xk сравнительно небольшое число наиболее информативных, т.е. уменьшить размерность наблюдаемого пространства.
В ряде процедур классификации (кластер-процедур) используют понятия расстояния между группами объектов и меры близости двух групп объектов.
Пусть Si i-я группа (класс, кластер), состоящая из ni объектов;
среднее арифметическое векторных наблюдений группы Si, т.е. центр тяжести;
(Sl, Sm) расстояние между группами Sl и Sm.
Наиболее употребительными расстояниями и мерами близости между классами объектов являются:
- расстояние, измеряемое по принципу ближайшего соседа: 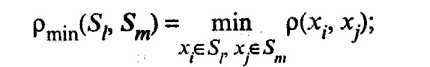(53.46)
- расстояние, измеряемое по принципу дальнего соседа:
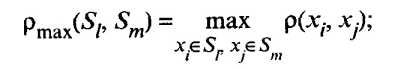(53.47)
- расстояние, измеряемое по центрам тяжести групп:
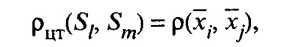(53.48)
где xl и xm векторы средних соответственно Sl и Sm кластеров; - расстояние, измеряемое по принципу средней связи, определяемое как среднее арифметическое всех попарных расстояний между представителями рассматриваемых групп: 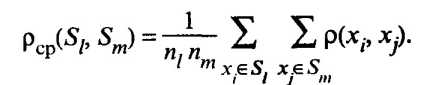(53.49)
Академиком А.Н. Колмогоровым было предложено обобщенное расстояние между классами, которое включает в себя в качестве частных случаев все рассмотренные выше виды расстояний. Расстояния между группами элементов особенно важный параметр в так называемых агломеративных иерархических кластер-процедурах, так как принцип работы таких алгоритмов состоит в последовательном объединении элементов, а затем и целых групп: сначала самых близких, а впоследствии все более и более отдаленных друг от друга. При этом расстояние между кластером Sl и кластером S(m,q), являющимся объединением двух других кластеров Sm и Sq можно определить по формуле 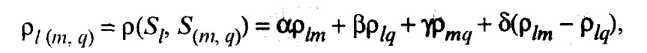(53.50)
где lm = (Sl, Sm); lq = (Sl, Sq) и mq = (Sm, Sq) - расстояния между кластерами Sl, Sm и Sq; , , и числовые коэффициенты, значения которых определяют специфику процедуры, ее алгоритм.
Например, при = = - = 1/2 и = 0 приходим к расстоянию, построенному по принципу ближайшего соседа. При = = = 1/2 и = 0 расстояние между классами определяется по принципу дальнего соседа, т.е. как расстояние между двумя самыми дальними элементами этих классов. Функционалы качества разбиения
Существует большое количество различных способов разбиения заданной совокупности элементов на классы. Поэтому представляет интерес задача сравнительного анализа качества этих способов разбиения Q(S), определенного на множестве всех возможных разбиений. Тогда под наилучшим разбиением S* понимаем такое разбиение, при котором достигается экстремум выбранного функционала качества. Следует отметить, что выбор того или иного функционала качества, как правило, опирается на эмпирические соображения.
Рассмотрим наиболее распространенный функционал качества разбиения. Пусть исследователем выбрана метрика в пространстве Х и пусть S = (S1, S2,..., Sp) некоторое фиксированное разбиение наблюдений x1, ..., xn на заданное число p классов S1, S2, ..., Sp.
За функционал качества берут сумму (взвешенную) внутриклассовых дисперсий 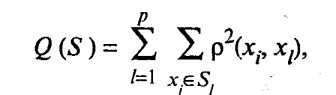(53.51)
где xl вектор средних для l-го кластера.
Иерархические кластер-процедуры
Иерархические (древообразные) процедуры являются наиболее распространенными (в смысле реализации на ЭВМ) алгоритмами кластерного анализа. Они бывают двух типов: агломеративные и дивизимные.

В агломеративных процедурах начальным является разбиение, состоящее из п одноэлементных классов, а конечным состоящее из одного класса; в дивизимных наоборот. Принцип работы иерархических агломеративных (дивизимных) процедур состоит в последовательном объединении (разделении) групп элементов, сначала самых близких (далеких), а затем все более отдаленных (близких) друг от друга. Большинство этих алгоритмов исходит из матрицы расстояний.
К недостаткам иерархических процедур следует отнести громоздкость их численной реализации. Алгоритмы требуют вычисления матрицы расстояний на каждом шаге, а следовательно, емкой машинной памяти и большого количества времени.

В этой связи реализация таких алгоритмов при числе наблюдений, большем нескольких сотен, нецелесообразна, а в ряде случаев и невозможна.
В качестве примера рассмотрим агломеративный иерархический алгоритм. На первом шаге алгоритма каждое наблюдение xi (i = 1, 2, ..., п) рассматривается как отдельный кластер.

В дальнейшем на каждом шаге работы алгоритма происходит объединение двух самых близких кластеров, и с учетом принятого расстояния по формуле пересчитывается матрица расстояний, размерность которой, очевидно, снижается на единицу. Работа алгоритма заканчивается, когда все наблюдения объединены в один класс.
Большинство программ, реализующих алгоритм иерархической классификации, предусматривает графическое представление результатов классификации в виде дендрограммы. Пример. Классификация стран по уровню жизни населения
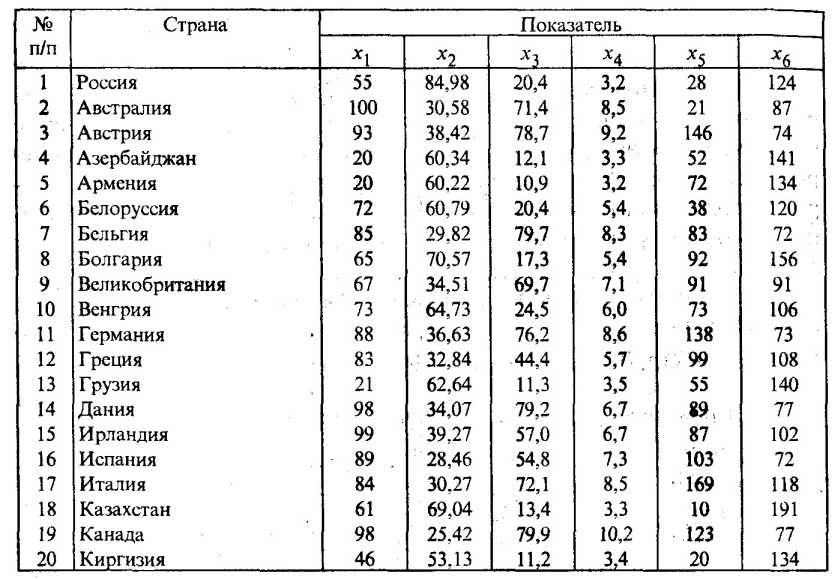
В табл. 53.4 представлены значения следующих шести показателей, характеризующих условия жизни населения двадцати стран в 1994 г.: x1 потребление мяса и мясопродуктов на душу населения (кг);
х2 смертность населения по причине болезни органов кровообращения на 100 тыс. человек;
х3 оценка валового внутреннего продукта по паритету покупательной способности в 1994 г. на душу населения (в % по отношению к США);
x4 расходы на здравоохранение (в % от ВВП);
x5 потребление фруктов и ягод на душу населения (кг);
x6 потребление хлебопродуктов на душу населения (кг).
Провести классификацию стран по уровню жизни населения и дать содержательную интерпретацию полученных результатов. Таблица 53.4 Макроэкономические показатели уровня жизни населения (1994 г.)
Решение. В условии задачи не оговорены число классов разбиения и вид законов распределения, а также не даны обучающие выборки.

В этой связи при классификации использовались методы кластерного анализа. Исходная информация (табл.

53.4) показывает, что в рассматриваемую совокупность входят страны бывшего СССР, Восточной Европы и промышленно развитые страны.

Поэтому можно предположить, что искомое разбиение стран по уровню жизни населения будет состоять из трех или четырех кластеров.
Классификация проводилась по различным алгоритмам кластерного анализа, но наилучшими в содержательном плане оказались результаты, полученные при разбиении стран на четыре класса.
В первый кластер вошли одиннадцать (n1 =11) стран: Австралия, Австрия, Бельгия, Великобритания, Германия, Греция, Дания, Ирландия, Испания, Италия, Канада. Наиболее удалена от центра этого кластера Италия, которая характеризуется самым высоким для кластера уровнем потребления фруктов (х5) и хлебопродуктов (x6).
Во второй кластер вошли четыре (п2 = 4) страны: Россия, Белоруссия, Казахстан и Киргизия.
В третий кластер вошли две (n3 = 2) страны: Болгария и Венгрия.
В четвертый кластер вошли три (п4 = 3) страны: Азербайджан, Армения и Грузия.
Средние значения показателей для четырех кластеров представлены на рис. 53.3 и в табл.

53.5. 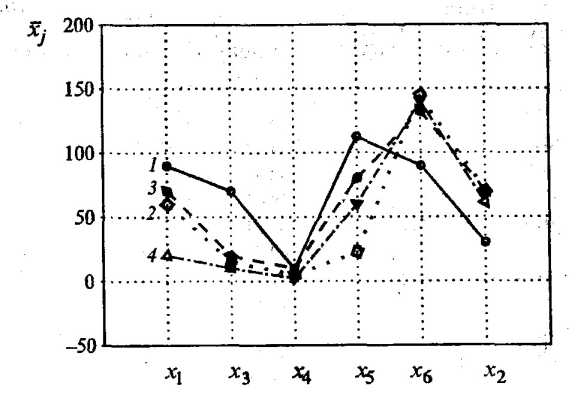Рис. 53.3. Средние значения показателей для каждого кластера (цифры у кривых соответствуют номерам кластеров) Таблица 53.5 Средние значения показателей
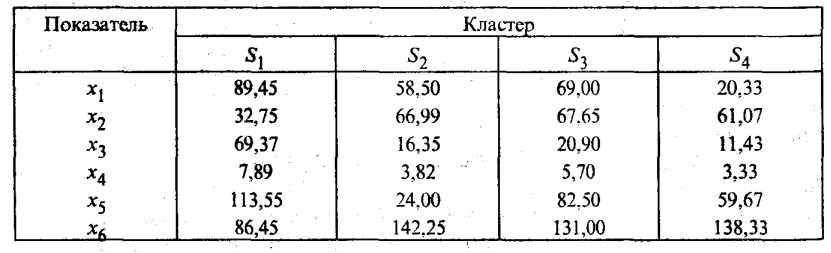
Кластер S1, в который входят промышленно развитые страны Запада, характеризуется (рис. 53.3) самыми высокими значениями: ВВП по паритету покупательной способности (x3), расходов на здравоохранение (х4), потребления мяса (x1) и фруктов (х5), а также самым низким значением смертности (х2). Самое высокое потребление хлебопродуктов на душу населения (х6) у стран, входящих в кластеры S2 и S4.
В кластер S4 вошли страны, на территории которых происходили в рассматриваемый период вооруженные конфликты. Этот кластер характеризуется самыми низкими средними значениями показателей х3 и х4, а также x1 среднедушевым потреблением мяса.
Заслуживает внимания матрица расстояний между центрами четырех кластеров:
Из матрицы следует, что кластеры S2, S3 и S4 примерно одинаково удалены друг от друга. Евклидово расстояние между ними равно соответственно 60,7; 53,0 и 55,5.

Наиболее выделяется по уровню жизни населения кластер S1.

Расстояния между S1 и кластерами S2, S3 и S4 равны соответственно 126,8; 83,3 и 120,6.
53.5. Основы эконометрики
Эконометрика это дисциплина, объединяющая совокупность теоретических результатов, методов и приемов, позволяющих на базе экономической теории, экономической статистики и математико-статистического инструментария получать количественное выражение качественных закономерностей. Курс эконометрики призван научить различным способам выражения связей и закономерностей через эконометрические модели и методы проверки их адекватности, основанные на данных наблюдений.

От математико-статистического эконометрический подход отличается тем вниманием, которое уделяется в нем вопросу соответствия выбранной модели изучаемому объекту, рассмотрению причин, приводящих к необходимости пересмотра модели на основе более точной системы представлений. Эконометрика занимается, по существу, статистическими выводами, т.е. использованием выборочной информации для получения некоторого представления о свойствах генеральной совокупности.

Наиболее распространенными эконометрическими моделями являются производственные функции и модели, описываемые системой одновременных уравнений.

Кратко остановимся на них.
Производственные функции
Производственная функция представляет собой математическую модель, характеризующую зависимость объема выпускаемой продукции от объема трудовых и материальных затрат. Модель может быть построена как для отдельной фирмы и отрасли, так и для всей национальной экономики. Рассмотрим производственную функцию, включающую два фактора производства затраты капитала К и трудовые затраты L, определяющие объем выпуска Q. Тогда можно записать

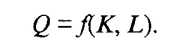
Определенного уровня выпуска можно достигнуть с помощью различного сочетания капитальных и трудовых затрат. Кривые, описываемые условиями j(K, L) = const., называются изо квантами. Обычно предполагается, что по мере роста значений одной из независимых переменных предельная норма замещения данного фактора производства уменьшается.

Поэтому при сохранении постоянного объема производства экономия одного вида затрат, связанная с увеличением затрат другого фактора, постепенно уменьшается.

На примере производственной функции Кобба Дугласа рассмотрим основные выводы, которые можно получить исходя из предложений о том или ином виде производственной функции. Производственная функция Кобба Дугласа, включающая два фактора производства, имеет вид
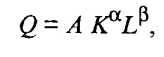(53.52)
где А, , параметры модели. Величина А зависит от единиц измерения Q, К и L, а также от эффективности производственного процесса.



Содержание раздела