Теория игр в нормальной форме

Теория игр в нормальной форме развита в более общих предположениях, индивидуальные функции полезности здесь не предполагаются траисферабельными и даже сравнимыми (см. гл. 1, II, III и VI, разд. 1 4). В данном случае мы ограничиваемся траисферабельными функциями единственно в целях простоты.

Ссылки на литературу по играм в характеристической форме без побочных платежей могут быть найдены в работе Аумана [1976].
Следующие два определения аналогичны определениям дележей и а-ядра для игр в нормальной форме.
Определение 8. Дележом в игре ? в ?-характеристической форме называется вектор x=(xt)ieN из Rw, для которого
2 Xi v(N), Х{^?({і}) для всех i?N.
іе л/
Обозначим через I (у) множество дележей игры (V, у).
Применяя итеративно условия супераддитивности (17), получаем
2 о ({/})* (Л).
ібЛ/
Для супераддитивных игр множество дележей I (?) не пусто. о({і})это уровень дохода, который игрок і может себе гарантировать сам. Поэтому ? ({і}) играет роль гарантированного выигрыша для игр в нормальной форме.

Доказательство леммы 2 подчеркивает прямую связь двух понятий дележа.
Если игра {N, ?) такова, что выполнено равенство 2 и ({}) =
ібЛ/
== ? (N), то множество / (у) состоит из одной точки, а игра (N, ?) называется несущественной (см. интерпретацию определения 5 гл. I). В этом случае из супераддитивности ? следует ее я дли-тивность (из (18)):
для всех S^N y(S) = 2 у({*})-
i € 5
(Доказательство этого факта оставляем читателю в качестве упражнения.) Для игр, не являющихся несущественными, ядро это возможно пустое подмножество дележей, стабилизируемых простыми угрозами.
Определение 9. Ядром игры (N, у) называется подмножество таких дележей х g / (у), для которых выполнено:
для всех коалиций S е N
2 ^o(S)- (19)
i€S 4 '
Будем обозначать ядро через С (у).
Пусть игроки договариваются о выборе кооперативного соглашения. Поскольку игра у супераддитивна, такое соглашение предполагает образование коалиции всех игроков N. Обсуждаться может только вопрос о способе дележа общего дохода v(N), т. е. о выборе вектора x?RN, для которого 2 x{ = v(N).
іеЛ/
Минимальным требованием для получения согласия игроков выбрать вектор х является индивидуальная рациональность этого вектора, т. е. условие хг^у({і}), і g N. Таким образом, игроки договариваются о выборе конкретного дележа х. Против выбора дележа х может возражать некоторая коалиция S, требуя для себя более выгодного распределения (например, t/g/(y), для которого у; х{ для всех і ? S). Коалиция S выдвигает это требование, угрожая в противном случае нарушить общую кооперацию (эта угроза вполне реальна, ибо для достижения дохода v(N) требуется единодушное согласие всех игроков). Предположим, что остальные игроки Se реагируют на эту угрозу отказом от всякой кооперации с членами коалиции S. После этого максимальный суммарный доход коалиции S оценивается числом y(S).

Условие (19) означает существование стабилизирующей угрозы коалиции S со стороны коалиции Sc. Таким образом, ядром игры (N, у) является множество устойчивых в смысле коалиционных угроз распределений числа v(N).
Кроме указанной интерпретации ядра с предостерегающими угрозами приведем эквивалентную интерпретацию с нормативной точки зрения.
Лемма 7. Пусть х?І (и)дележ игры (N, у), х принадлежит ядру е том и только том случае, когда для всех коалиций ScN выполнено
Доказательство. Поскольку 2 xi = v(N), то приведенное
Выше неравенство можно переписать так:
0(SC) 2 */¦ ' і е s
Пример 7 (продолжение).
Вектор х = (xs, хр, xD) в игре ,джаз-оркестр" принадлежит ядру тогда и только тогда, когда
Это множество является выпуклой оболочкой следующих трех дележей:
(350, 450, 200) (350, 500, 150) (300, 500, 200).
Таким образом, выигрыши всех игроков определяются с точностью до 50 $. Типичным представителем ядра является центр (среднее арифметическое крайних точек) множества С (?), а именно:
х* (333.3, 483.3, 183.3)
Для дележа х* характерно, что все двухэлементные коалиции имеют одинаковый дополнительный доход: х(-\-х{?({і, /}) = = 16.6 $. Дележ х* является справедливым компромиссом внутри С(?).
Из того, что ядро пусто, не следует невозможность кооперации всех игроков N. Это означает просто, что никакой дележ не может быть стабилизирован с помощью простых, естественных угроз, описанных выше. В этом случае кооперативная устойчивость требует более сложного поведенческого сценария подобно угрозам и контругрозам, описанным в разд.

2 (см., в частности, задачу 3). На этом пути мы придем к концепции переговорного множества, предложенной в работе Аумана, Машлера [1964].
Пустота ядра наблюдается в том случае, когда промежуточные коалиции слишком сильны. Это утверждение проясняется следующим примером.
Пример 8. Симметричные игры
В симметричной игре коалиции с одинаковым числом игроков имеют одинаковый выигрыш. Характеристическая форма о
Гл. ?і. СтабилЬнодМЬ ДО дбнобе ytpM
Имеет следующий вид:
? (S) = ?? (s), где s = I $ I для всех ScAf.
Предположим без потери общности, что у*(1) = 0 и N = { 1, 2, Тогда множеством дележей игры у* является сле
дующий симплекс в Rn:*€ / (?*) ФФ 2 = у* (я), *(0, і = 1, .... п.
; =1
Ядром С (у*) является подмножество / (о*), определенное конечным числом (точнее: 2Пп2) линейных неравенств (19).

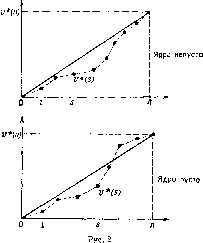
Таким образом, ядроэто, возможно, пустой, выпуклый многогранник внутри симплекса / (у*) *). В силу симметричности у ядро С (у*) тоже симметрично, т. е. инвариантно при любой перестановке компонент х? ..., хп.

Учитывая, кроме того, выпуклость С (у*), получаем, что множество С (у*) не пусто в том и только в том случае, когда оно содержит центр х* множества / (у*), а именно xf=*l/n, і 1.....п. Возвращаясь к системе (19), получаем, что
[С(н*)#0]^ для всех s=l, .... п -і- v* (s) ^ v* (п) j .
Таким образом, ядро С (?*) не пусто тогда и только тогда, когда не существует промежуточной коалиции S, в которой средняя доля каждого игрока больше соответствующей величины в коалиции N.
Возвращаясь к общему случаю, охарактеризуем непустоту ядра с помощью линейного программирования.
Определение 10. Для данного множества N обозначим через Р (і) множество коалиций, содержащих игрока і:
Сбалансированным семейством коалиций) назовем отображение б из P(N) в [0, 1], для которого
для всех i?N 2 1.
SeP( о
Наконец, игру в характеристической форме (N, ?) назовем сбалансированной, если
2 бои (S) ? (N) для всех сбалансированных семейств
S6P(N)
коалиций б. (20)
Теорема 2 (Бондарева [1962], Скарф [1967]). Игра (N, ?) имеет непустое ядро тогда и только тогда, когда она сбалансирована.
Доказательство. Пусть xgC(?), а бсбалансированное семейство коалиций, тогда
х (S) ^ ? (S) = ?sx (S) ^ 6so (S) для всех SczN. Суммируя эти неравенства, получаем
2
SeP(A/)2 6sx(S)=2 2 sxi = 2*,-=у(Л0-
SePlN) te N Se p (0 ieN
Ssv (S)
Наоборот, если ядро С (v) пусто, то система линейных неравенств-*(#)a (N),
x(S)^v (S) для всех S с N
не имеет решения. Используя стандартные рассуждения (теорему двойственности), получаем, что для всех S найдется неотрица-
9 Соответствует термину сбалансированное покрытие. Прим, перев.
тельное число 6S, такое, что:
для всех д:$RNy\ Х:= 2 65(2*Л и
іел/ SeP(N) \ies )
2 6so (S) v (N).
SeP(N)
Первое из этих свойств эквивалентно тому, что бсбалансированное семейство коалиций, что и завершает доказательство теоремы 2.
В качестве приложения теоремы 2 рассмотрим игру трех лиц I N I = 3. Каждому разбиению N соответствует тривиальное сбалансированное семейство коалиций:
разбиение N: 6^=1, 6S = 0 для всех S=?N,
разбиение {/}{/?}: б{1} = 1, = 1, 6S = 0 в остальных случаях.
Применяя условие (18) к этим б, получаем условие супе-радднтивности игры ?
?(і) + ! для всех {/, /, 6} = {1, 2, 3}. (21)
Далее, коалиционной структуре {12}, {23}, {31} соответствует сбалансированное семейство коалиций б*6*} = ?2 Для всех *. /. ‘ Ф /,
6* = 0 в остальных случаях.
Применяя (20) к б*, получаем
о(12) + о(23) + о(31)2о(123). (22)
Пусть теперь читатель убедится в том, что все сбалансированные семейства коалиций для N являются выпуклыми комбинациями б^, б‘ !/'* и 6*. Следовательно, непустота множества С(?) характеризуется системой неравенств (21), (22).
Следствие из теоремы 2. Любая супераддитивная игра трех лиц имеет непустое ядро тогда и только тогда, когда выполнено (22).
При увеличении числа игроков проверять сбалансированность игры ? становится все труднее). Например, супераддитивная игра четырех лиц обладает непустым ядром в том и только том случае, когда
? (12) + ? (23) ? (34j -ф ? (41) ^2о(1234), ? (123) + ? (234) + ? (134) + ? (124) З? (1234), о(123) + ? (234) + о (14) 2 (1234),
а также выполнены пять аналогичных неравенств, которые получаются из данных перестановкой игроков.
Упражнение 11. Докажите сформулированное выше утверждение.
Задача 8, приведенная ниже, иллюстрирует типичное приложение теоремы 2 к экономическим моделям.
Задача 6. Ядро в простых играх
Игру (N, ?) назовем простой, если
для всех S^N v(S)~0 или 1.
Обозначим через W множество выигрывающих коалиций, т. е,S€W^y(S) = l
1) Докажите, что игра (N, ?) супераддитивна тогда и только тогда, когда подмножество W множества всех коалиций является монотонным и собственным:
S?W, S=T=bTeW для всех S, Г,
sewzs*$w.
2) Игрока i*?N назовем диктатором W, если {/?} выигрывающая коалиция!{*} € W,
Полагая игру (N, ?) супераддитивной, докажите, что W имеет (единственного) диктатора тогда и только тогда, когда игра несущественна.
3) Пусть W не пусто и не имеет диктатора. Игрока і* назовем вето-игроком, если N\{i*} не является выигрывающей коалицией.

Обозначим через N+ возможно пустое множество вето-игроков.
Докажите, что ядро С (о) не пусто тогда и только тогда, когда не пусто множество N+. В этом случае докажите, что

х{ = 0 для всех і (? N+, Xf^O для всех і € N .
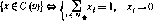
4) Пусть для каждого і голос игрока і имеет вес qt ^ 0. Обозначим через q0 такое число, что
7о 2 q{ 2?о-
і 6 N
Определим взвешенную мажоритарную игру Wq следующим образом:? € Wq фф 2 9; ^ q0.itS
Докажите, что Wq монотонная и собственная простая игра. Докажите, что в этой игре игрок і* является диктатором тогда
и только тогда, когда q0 ^ q.*t и і* является вето-игроком в том и только том случае, если
ItN
5) Сравните полученные результаты с задачей 1 Гл. VI. Задача 7. Выпуклые игры


Пусть (N, ?)выпуклая игра, т. е. такая, для которой справедливо
o(S)-fо(Т);о(SЛТ)-fy(SU'T) для всех S, ГдЛ/.
I) Докажите, что
v(N)v(Sc)= sup {o(SuT’) о (Г)} для всех SczN.
Tc=Sc
Сопоставьте этот факт с утверждением леммы 7.
2) Для любого порядка 1, 2, ..., п в N рассмотрим вектор
*/ = (!, 2.....2, ..., г 1), t= 2.....п.
Докажите, что х принадлежит ядру игры (N, ?).
3) Докажите, что С(?) является выпуклой оболочкой дележей ха, полученных в 2), при условии, что а принимает значение всех возможных порядков в N.
Задача 8. Ядро экономики обмена
Пусть для всех і 6 N ut функция полезности, определенная в неотрицательном ортанте IR?. Мы интерпретируем г ? как вектор потребления, а иг (г) полезность для игрока і вектора г. Обозначим через wt g начальный запас товаров у игрока і.
Игру экономика обмена (с побочными платежами) с функциями (и,, i g N) определим следующим образом:
для всех S^N v (S) = sup J 2 и,- (г,-) 2гг= 2 we, гі€К?і.
(fsS ieS ieS J
1) Предположим сначала, что p=l и N B()S, где для і?В (покупатель) w{ 0, а для igS (продавец) wt= 1.
Пусть функция щ имеет следующий вид:
если і € В
( uf(z) = если /gS
I ujiz) =
( и?(г) = 0 для г 1,
для z 1, U/(z) = S/ ДЛЯ 2 1, О ДЛЯ 2^1.
\ ui(z) = bt
Упорядочим В и S так, что
Ьпь .?J для і'?В = {1, .... пь},
Sj .. ,s, . .smi для j?S = { 1, ..., ms}.
Докажите, что v(N) = ^ (bis;), где t наибольшее целое
1
число, для которого iinf(n6, ms),
Докажите, что если дележ х принадлежит ядру С (у), то должна существовать цена q, такая, что
хі Ь{ q Для і?В, і,
- 0 для i?B, t (?,
*qS/ для jS, //,
= 0 для i?S, / i.
(го)
(23')
Найдите интервал I = [qini, gSUp], обладающий таким свойством: для q ?І дележ (23) принадлежит С (v).
Докажите, что все цены конкурентных равновесий этой экономики обмена принадлежат интервалу /.
2) Пусть теперь рпроизвольное натуральное число и для всех і ? N Uj вогнутая функция, определенная на К?.
Докажите, что игра (N, ?) является сбалансированной и, следовательно, имеет непустое ядро. Докажите, что конкурентное равновесие принадлежит ядру С(?).
ЛИТЕРАТУРА
Арои (Aron R.)
[1962] Paix et guerre entre les nations. Paris, Caiman - Levy Ed. Ауман (Aumann R. J.)
[1976] Lecture on game theory, Stanford, Stanford University, IMSSS
[1978] Survey on repeated games. Stanford, Stanford University, IMSSS. Ауман, Машлер (Aumann R. J-, Maschler M.)
[1964] The bargaining set for cooperative games. Advances in Game Theory, Annals of Math.

Studies n 52, Princeton N. J., Princeton University Press.
- Берж К-
[1962] Теория графов и ее применения. М.: ИЛ.
Бондарева О. Н.
[1962] Теория ядра в игре п лиц. Вестник ЛГУ, сер. мат., мех., астрон., 13, 3, 141142 '- 'Васин А. А.
[1978] Сильные ситуации равновесия в некоторых сверхиграх. Вестник МГУ, сер. мат., мех., 1, 30 40
[1983] Модели процессов с несколькими участниками.М.: Издательство МГУ.
Викри (Vickrey W. S.)
[1959] Self-policing properties of certain imputations sets. Annals of Math.
Studies 40, Princeton, Princeton University Press.
- Гермейер Ю. Б.
[1973] К теории игр трех лиц. ЖВМ и МФ, 13, 6, 14591468.
Термейер Ю. Б., Штильман М. С.
[1975] Некооперативные повторяющиеся игры с произвольным дисконтиро-. ванием. ДАН, 211, 1, 2225 - Кукушкин Н. С.
[1974] Точки равновесия в метаиграх. ЖВМ и МФ, 14, 2, 312320.
Льюс, Райфа (Luce R. D., Raiffa Н.)
[1957] см. литературу гл. I.
- Меньшиков И. С.
[1977] Стационарные стратегии в играх со скользящим дисконтированием.
Вестник МГУ, сер. мат., мех., 4, 1017.
- Меньшикова О. Р.
[1976] Крайние точки С-ядра симметрических игр. Вестник МГУ, серия мат., мех., 5, 6372.
[1977] Методы поиска ядер кооперативных игр и их приложения. Диссертация, Московский университет.
- Миркин Б. Г.

" ' эуппового выбора. М.: Наука.
[1977] Cours de theorie des jeux a deux joueurs. Cahier de Mathematiques de la Decision n 7709, Paris, Universite Dauphine.
Мулен, Пелег (Moulin H., Peleg B.)
[1982] Stability and implementation of effectivity functions, Journal of Mathematical Economics 10, 1, 115145.
Мулен (Moulin H.)
[1981] см. литературу к введению Накамура (Nakamura К.)
[1979] The vetoers in a simple game with ordinal preferences. International Journal of Game Theory, 8, 1, 5561,
- Ope O.
[1980] Теория графов. M.: Наука.
- Оуэн Г.
[1971] см. литературу гл. IV. .
Розенталь (Rosenthal R.)
5, 1.
[1972] Cooperative games in effectiveness form. Journal of Economic Theory,
Рот (Roth А.)
[1976] Subsolution and the supercore of cooperative games, Mathematics for Operation Research, 1, 1.
Рубинштейн (Rubinstein A.)
[1979] Equilibrium in supergame with the overtaking criterion, Journal of Economic Theory, 21, 1, 19.
Сен (Sen A.)
[1970] Collective Choice and Social Welfare, San Francisco, Holden Day, Снарф (Scarf H.)
[1967] The core of an N-person game. Econometrics, 35, 5069,
Ховард (Howard N.)
[1971] Paradoxes oi rationality: theory of metagames and political behaviour, Cambridge (USA), M. I. T. Press,
Шеллинг (Schelliig T. C.)
[1971] см. литературу гл. III.
Шерер (Sherer F. M.)
[1970] см. литературу гл. V.
Яиг (Young H. P.)
[1979] The market value of a game, II AS A working paper, Laxenburg,
УКАЗАТЕЛЬ
Арон 155 аукцион 20
Викри 21
второго типа 21, 77
неделимого товара 20, 82
первого типа 20, 82
Ауман 137, НО, 170, 173, 186, 188
агентов по продаже автомобилей 81, 95
аукцион 125
вежливые водители 138
джаз-оркестр 185
китайский покер 119, 128
мариеибадская 51
*¦ музыкальные стулья 142
Ним 50
переговоры 135 * перекресток 139
в смешанных стратегиях 104
пиратские корабли 132
раз-два-игра 33, 101
размещение магазинов 121, 137
с нулевой суммой 3037, 4952, 79, 82. 107, 117
таможенный досмотр 117
торг 156
индивидуально рациональный исход 72, І55
исход игры 15
Берж 67, 78
биматричиые игры 110117 Бинмор 64 блеф 106 Бондарева 190
борьба за лидерство 57, 74, 178, 182
право второго хода 182
первого хода 182 Брамс 14
Брауэр 36
Вебер 83 ведомый 53 Виал 147 Викри 164
война иа истощение 83, 84, 93, 94, 126 Вулф 124
выборы большинством голосов 38 40, 161, 164, 167
- о правом вето 4143, 76 выпуклые игры 194
Кларка Гроувза механизм 24 Кнастера Куратовскоео^т Мазуркееича лемма 78
Кондорсе 9, 161
парадокс 161 контругроза 168 Кун 46
алгоритм 46
теорема 46 Курно 91, 84
-* процедура нащупывания 8495
Габе 89, 92
гарантированный выигрыш 27, 103, 138 Гильбо 99 Гликсбере 121
голосование по Ролсу 5557
Лексикографически осторожная страте гия 29 лидер 53 лидерство 53 лотерея 101
¦ индивидуальная (собственная) 101 совместная 141 Льюс 19, 102. 164
Данфорд 121
двоичный выбор с взаимным влиянием Дележ 156, 175, 186 дерево 43
дилемма^ заключенного 19, 104, 153,
локальная 9697 Дживерс 58
доминирование по Парето 20
стратегий 16 доминирующая стратегия 17 Дутта 58
дуополия 22, 81, 8487, 95, 145, 178 дуаль 34
бесшумная 35
топологическая 52
шумная 34
Машлер 188
Метод дели-выбирай 64 методы дележа 59 парадоксальный 62 Милером 83 Мон мор 100
Ыулен 14, 23, 29. 35, 65,
89, 92, 95,
118. 147. 149, 163. 164.

168. 184
Наилучший ответ 31. 85, 88, 109
отображение 53, 85, 177 Накамура 166
недоминируемая стратегия 16 фон Нейман 79, 164 несущественная игра 27
квази 183 *¦ тт ПОЧТИ 77
Жерар-Варе 149
Игра о нулевой суммой 3037, 4952, 79, 82 107, 117 игра 15
нормальная форма 15
игра в 15
носитель смешанной стратегии 108, 112 Нэш 69
равновесие 69, 87, 90
теорема 78, 102
сильные равновесия 134 смешанное расширение игры 101 смешанные стратегии 101
вполне 108 соглашение 131
необязательное 131 132, 148
стабильное 131, 142, 147149 стратегия 15
стратегическая обоснованность голосования с упорядочением 23 сценарий предостережений 154
Олигополия 2223, 80, 9495 Окугучи 89 Ортега 98
осторожная стратегия 26, 106
Тийс 124 Угрозы 154
устойчивое равновесие 8788 локально 89
Партхаоаратхи 108, 124 Пемг 167
повторяющиеся игры 171 173 полная информация 44 последовательное исключение Доминируемых стратегий 40 почти для всех игр 111 предостережение 154 сценарий 154 предупреждение 158
Фаркуарсон 14, 38
финансирование общественных нужд по добровольной подписке 82
Характеристическая функция 188 игра в форме 185
Равновесие
в доминирующих стратегиях 17
в смешанных стратегиях 102
в совместных смешанных стратегиях 140
по Нэшу 69
по Штакельбергу 53
сильное 134
слабое 147
сложное 40 Рагхаван 108, 124
разрешимость по доминированию 40
локальная 92 Райез 100 Райфа 19, 102, 164 редуцированная игра 45 Рейнбольдт 98
Розен 85 Розенталь 164 Рот 164 Роше 48
Рубинштейн 67, 170 Рудин 123 Рэнд 87
Цена игры 30
--с нулевой суммой 3031
в смешанных стратегиях 79 Цермело 50
Шахматы 50 Шеедиауэр 14 Шеллинг 70, 74, 178 Шварц 121 Шепли 36 Штакельберг 53 Штейнгауя 59 Шоттер 14
Эквивалентные стратегии 18 экономика обмена 193
ос-ядро 160, 175 р-ядро 169, 182 у-ядро 176, 182 Яне 185
Сайон 124
седловая пара (стратегий) 31, 79 Сен 163

ОГЛАВЛЕНИЕ

Предисловие редактора перевода , . .
Предисловие......... . , . .
Введение...............
Часть I. Некооперативное поведение игроков 4. Поведение лидера и ведомого ................ со
67 84 6. Другие приложения теоремы Куна
Литература........................
Глава III. Равновесие по Нэшу ...............
1. Определение и обсуждение.................
2. Теорема Нэша о существовании равновесий .........
3. Устойчивые равновесия ..................
Литература ,, ...................... Глава IV. Смешанные стратегии
1. Смешанное расширение игры . ................
2. Вычисление равновесий по Нэшу в смешанных стратегиях , , ,
3. Бесконечные игры
Литература ..9.*...*.........*. Часть II. Кооперативное поведение игроков , 1. Сильное равновесие ...................... Литература.........................
Глава VI. Стабильность иа основе угроз ............
*) В отечественной литературе используется также термин абсолютно оптимальная стратегия, Прим, перев. ) Для существования такой меры достаточно, чтобы в Ху существовало счетное всюду плотное подмножество. Прим, перев. ) Правило голосования называют стратегически обоснованным, если в соответствующей этому правилу игре существует равновесие в доминирующих стратегиях при всех предпочтениях участников из некоторого заданного класса. Прим, перев Функция выигрыша каждого игрока в игре g является суперпозицией отображения я, формализующего правило голосования и функции полезности, заданной на множестве кандидатов А. Прим, перев. ) Функция / (х) называется полунепрерывной сверху, если для любого Я множество {* \ f (x)^ Я) замкнуто. Полунепрерывность сверху функции ? (yt) следует из непрерывности функции к/ (*) в силу равенства
{УХ/1 ? (yt) SS Я) = П {Уі1 ui (Уі xi) ^ M-
КЛХІ
Для случая метрического пространства Лл функция ? (у/,-) является непрерывной. П рим перев. ) Приведем пример несущественной игры. Предположим, что игроки
{1.....п} используют следующую процедуру дележа. Игра проводится в
п этапов. На первом этапе игрок 1 объявляет, что он претендует на некоторую долю *х1.

Игрок 2 можете этим согласиться, а может объявить, что он претендует на некоторую долю х2 л^. Далее игрок 3 может либо принять предложение игрока 2, либо сделать собственную заявку х$ хг и т. д.
На первом этапе игрок і, чья заявка дг,- дг,-_і будет принята игроками і+1, - - - п, получит долю товара дг,- и выйдет из игры. Для остальных игроков повторяется описанная процедура. На этапе п1 остается два игрока.

На последнем этапе п остается один игрок, который и забирает остаток товара. На этом игра кончается.
Нетрудно убедиться в том, что гарантированный выигрыш любого игрока равен 1 /п, а потому игра несущественна и ее исходом является справедливый дележ. Эту игру удобно представлять как игру в развернутой форме.

См. гл. II.

Прим, перев. ) Сходимость последовательностей наилучших ответов подробно исследована в разд. 3 гл.

III. Прим, перев, ) Еще сильнее ограничивает длину партии правило, по которому засчитывается ничья после 50 ходов без продвижения пешки или взятия фигур. Прим, перев. ) Можно представлять себе, что имеется куча из п камешков. В игре G„ игрок 1 произвольно делит кучу на две части, а игрок 2 выбирает одну из них и начинается игра G, и т. д. ... Игрок, выбравший часть, состриг (цую из одного камешка, выигрывает.

Прим, перев. Звездочкой отмечены работы, добавленные при переводе. ) Такие процедуры принятия решений соответствуют гипотезе об ограниченной рациональности участников, не заглядывающих в будущее. Прим, перев. ) Утверждение леммы 1 можно усилить, заменив о,- на 0/ =* *= inf sup щ(уі, у,) а,-. Прим, пврев, Это утверждение неверно, как показывает следующий пример, построенный В. А. Гурвичем. ^Рассмотрим игру четырех лиц с функциями Дайте интерпретацию этого уравнения как непрерывной Версии процедуры нащупывания по Курно. Любой NE-исход х* игры G является неподвижной точкой (15). Найдите почти совпадающие необходимые и достаточные условия (выраженные в терминах оператора Т) того, что 563 - Звездочкой отмечены работы, добавленные при переводе. ) На самом деле, современник Монмора Джеймс Уолдгрейв предложил в аналогичной игре использовать смешанные стратегии. Не ясно, однако имел ли он хотя бы интуитивные представления об оптимальных смешанных стратегиях (см. исторический очерк Райвз [1975]). ) Напомним, что в R существуют замкнутые подмножества без внутренних точек, мера Лебега которых отлична от нуля (и даже такие, дополнение к которым имеет меру не более произвольного е 0). ) К тому же нечетно (см, Харшаньи [1975)). В случае затруднения см. Оуэн [1971] (пример П. 5.9).

Прим, перев. Звездочкой отмечены работы, добавленные при переводе. ) В оригинале doomsday machine.Прим, перев. а) С игрой S из гл. II иа самом деле совпадает игра S (2; 0).~Прим, перев, Правильной простой игрой здесь называется монотонная и суперад-дитнвиая простая игра (см. Оуэн [1971]), Прим, перев. *) См. в Берж {1962], Ope [1980]. Прим, перев. ) Похожий анализ игры трех лиц сі- в работе Гермейера [1973], Прим, перев. По этому вопросу см. также Васин [1978], Васин [1983.] Примй перев. ) Аналогичные условия получены в работе Гермейер, Штильмаи [1976J. В некоторых случаях рассмотрение стационарных стратегий в памятью на один ход не ограничивает общность рассуждений (см. Меньшиков [1977]), Прим, перев. ) Величина у,- характеризует максимальный гарантированный выигрыш лидера (игрока і) без предположения благожелательности ведомого.Прим. перее. ) Из доказательства теоремы 1 следует, что класс III естественным образом разбивается на четыре группы игр.
lllj. CpfCv=Cp. В этом случае, как и для игр класса II, ведомым быть лучше, чем лидером, так как Однако теперь возможен компро
мисс, при котором у лидера нет оснований отказываться от лидерства.
1112. 0^00^= ? Лидером быть лучше (ySsp), но возможен компромисс, устраняющий опасность захвата лидерства ведомым игроком.
1113. СрПС? = Оі = (х I і (x)5s Yi "2 (*) S* p2}- „Естественным лидером в играх этой группы следует считать игрока 1.
1114. Cpf)Cy = D2~ {х I и2 (х) S? уз, j (х) Эг Pi}.

Случай, симметричный ІІІ8. Компромисс фактически сводится к выбору лидером игрока 2. Прим, пере?. ) Крайние точки ядра симметричной игры описаны в работе Меньшикова [1976]. Прим, перев. ) Это объясняется тем, что сбалансированных семейств коалиций (сбалансированных покрытий) становится слишком много. Их полное описание при I /V I С 6 см. в работе Меньшикова [1977].

Прим, перев. Звездочкой отмечены работы, добавленные при переводе.

Содержание раздела

---