СМЕШАННЫЕ СТРАТЕГИИ
В неравенствах из (13) просто сравниваются модули наклонов касательных к кривым BRt и BR2 в точке х*. Положим
s. = д2ы,- /¦ дЧ(
' дх; дХі I дх; дх? ‘
Тогда неравенства (13) можно переписать в следующем виде:
I sj I I s21 = х* локально устойчива,
Sj ) s21 = лг*' не является локально устойчивой.
Для случая б) примера 5 получается неустойчивое равновесие по Нэшу, поскольку I Sj I I s, , причем sx- и s2 одного
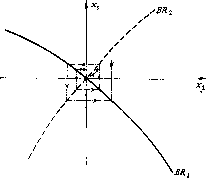
знака. Если s21 и sf, s2 положительны, то получаемобычную нестабильность типа паутины, изображенную на рис. 7.
Если, напротив, Sjs2, то может быть показано, что локально устойчивое равновесие по Нэшу х* является единственным сложным равновесием для усеченной на достаточно малую прямоугольную окрестность х* начальной игры. Проиллюстрируем этот факт на следующем рисунке.
Начинаем с игры ([a*, f)1], [a2, b2], uit u2), выбрав числа a,-, bi так, чтобы ut была вогнута по х{ на [а*, Ь^х[а2хЬ2]. Затем замечаем, что при любом фиксированном х2%[а2, Ь2] выигрыш і (- , х2) возрастает на отрезке от at до гх (х2), затем убывает на [Гі (х2), 6,]. Поскольку rt (x2) ? [cj, df] для всех х2€[а2, Ь2], то отсюда следует, что любая стратегия хг ? [al, cf] игрока 1 доминируется его стратегией си в то время как любая стратегия xf € (df, Ь±] доминируется стратегией d,.
Отбрасывая доминируемые стратегии игрока 1, получаем игру ([cj, dj, [а2, b2], и? и2), в которой в силу аналогичных рассуждений множество недоминируемых стратегий игрока 2отрезок [с2, d2]. Таким образом, получается редуцированная игра ([с4, dj], [с„ d2], ult и2). Если продолжить итеративно эту операцию, то
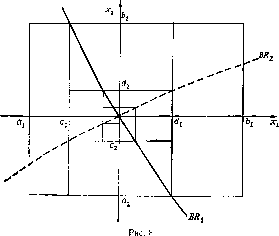
станет ясно, что множества стратегий стягиваются к устойчивому NE-исходу х, как это видно из рис. 8.
Связь между локальной устойчивостью и локальной разрешимостью по доминированию на самом деле является весьма общей. Скажем, что игра G локально разрешима по доминированию в х?, если существует прямоугольная окрестность Кд, точки х?, такая, что усечение игры G на Кд, обладает следующим свойством: последовательное исключение доминируемых стратегий стягивает Кд, в пределе к х. Тогда в предположении теоремы 3 в работе Габе, Мулен [1980] доказано, что а) Если все собственные числа оператора Т по модулю меньше 1, то игра G локально разрешима по доминированию в х.)
б) Если игра G локально разрешима по доминированию в х*, то абсолютная величина любого собственного числа оператора Т не превосходит I.
Замечание. На рис. 8 мы исключаем доминируемые стратегии последовательно сначала у одного игрока, потом у другого.
По лемме 3 гл. II (обобщенной на данный случай) получается в точности то же самое, что и при одновременном исключении.
Как мы видели в упр. 6, для процедуры нащупывания по Курно это не так.
Упражнение 7.
Для игры трех лиц, в которой множества стратегий всех игроков одномерны, приведите почти совпадающие необходимые и достаточные условия локальной {1, 2, 3}-устойчивости, аналогичные условиям теоремы 3.
Упражнение 8.
В детерминированном варианте войны на истощение (пункт 1 задачи 5) вычислите множества наилучших ответов BR; (в данном случае они не являются кривыми размерности 1) и проанализируйте устойчивость процедуры нащупывания по Курно. Обратите особое внимание на процедуру нащупывания, начинающуюся из (0, 0), и дайте интерпретацию этой процедуре как схеме эскалации.
Далее рассмотрите вариант войны на истощение, в котором каждый игрок не может обнаружить агрессивность противника: стратегия х,- игрока і означает, что игрок і решает раз и навсегда быть агрессивным до момента / = х;. Тогда получаем игру в нормальной форме:
*X
Л._у 2 х*
xz) =
при х3 хь при X, х„
при xt = xt.
Функция и2 определяется аналогично.
Докажите, что в этой игре нет Л^Д-исходов и проанализируйте процедуру нащупывания по Курно. Сравните с игрой Война на истощение.
Задача 5. Устойчивость в олигополии с назначением выпусков
Обобщим пример 4 за счет введения функции затрат с,- (у) на производство у единиц товара производителем і. Тогда возникает игра
Х,. = [0, +оо), иі(х) = хір (х)сі(хі), і ? N.
На функцию р наложим ограничения (7). О функциях с{ мы просто предположим 0.
Значит, затраты на выпуск единицы продукции могут быть возрастающей, убывающей или вообще немонотонной функцией величины у.
Пусть у каждого игрока затраты на выпуск единицы продукции возрастают или не слишком сильно убывают в следующем смысле:
с1(у)2р' (у) + у-р (у) при г/5? 0, і'=1, .... п. (14)
Покажите, что существует по крайней мере один NE-исход.
2) С этого момента предположим существование NE-исхода х?, не требуя обязательного выполнения (14).
Докажите, что исход х* локально устойчив, если выполнены следующие неравенства:
с] (xf) (ft3) I р' (х*) I + (п2) I р (х*) I-xf.
Указание. Полагая
Р'(**)+Р (**)- **
Рі V (**) + р (х*) ¦ xf с\ (xf) ’
докажите, что 0р,-1 при всех t = 1, ..., п (принимая во внимание, что п^ 2). Далее заметьте, что собственное число X оператора Т либо равно р,- для некоторого і = 1, .п, либо является решением уравнения
РІ I I Рп _ I
%-\-Pi Х-\-рп
3) Пусть все игроки идентичны (с{ = с для всех і = 1, п) и х*равновесие по Нэшу на диагонали: xf = xf = г/*. Докажите утверждение, обратное сформулированному в п. 2. Если выполнены неравенства
2р' + у*.р с (п3)р’\ + (п2)¦/*- !р\
(где все р' и р взяты при х* пу*, а с взята в /?), то дг* не является устойчивым NE-исходом. Заметьте, что для NE-исхода г* выполнено неравенство 2р' + у*р с, поскольку функция ut от аргумента х( достигает максимума в точке х*.
Следовательно, устойчивость исхода х? всегда имеет место для п = 2 и требует выполнения все более жестких условий с ростом п.
Задача 6
1) Докажите, что в игре агентов по продаже автомобилей (задача 2) нулевой NE-исход не устойчив.
2) Для ненулевого N ^-исхода докажите, что оператор, опре-деленный по формуле (11), всегда имеет собственное число, равное 1. Используя ту же технику, что и в задаче 5, докажите, что этот исход не является локально устойчивым, если по крайней мере для двух агентов выполнено неравенство
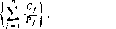
3) В случае п = 2 докажите непосредственно (т. е. найдя BRt и BR2 и нанеся их на рисунок), что ненулевой і?Д-исход устойчив. Аналогично проанализируйте устойчивость Л^Д-исхода в дуополии с назначением выпусков из упражнения 4.
Задача 7. Процедура нащупывания по Курно в непрерывном времени (Мулен [1977])
Пусть G = (л,-, up, і ? N) игра п лиц, в которой каждое множество стратегий одномерно. Пусть рдействительная функция, определенная на R, причем
Ф (0) = 0, ф' (/) 0 при t € R.
Допустим, что функция и{ дважды непрерывно дифференцируема на XN при всех і € Рассмотрим следующее дифференциальное уравнение на XN: dx1
= Ф (ri (xi)X/) для всех i 6 N. (15)
^?устойчивое решение (15) (т. е. найдется окрестность V точки л-*, такая, что система (15) с начальным условием из V порождает траекторию, которая не покидает V и сходится к х?). Докажите, в частности, что если х?локально устойчивый ЛХЕ-исход (определение 3), то он является устойчивым решением (15).
Приведите пример, показывающий, что обратное утверждение не верно.
Задача 8. Локальная дилемма заключенного (Мулен [1979]) 1) Фиксируем пх/г-матрицу Л = /=1.....„ и предполо
жим, что аиФ 0 при всех 7=1, ..., п. Для данных Xt 0, ... Х„ О обозначим через G (Л; X) игру (У, (X,.), и,; і = 1, ..., п), где [hI ^/] Для всех 7=1, п,
В игре G (Л; X) каждый игрок имеет единственную доминирующую стратегию. Обозначим через х (X) ? Yn (X) равновесие в доминирующих стратегиях. Докажите, что следующие четыре утверждения эквивалентны:
1) Для всех К 0 исход х (X) не является оптимальным по Парето в G (Л; X).
2) Для некоторого X 0 исход х (к) не является оптимальным по Парето в G (Л; X).
3) Существует вектор xglR, такой, что
Щ (хі'еі) 01 ,
,*)о; длявсех‘-.......
где в, = (0, О, 1^, 0, .... 0)€RB.
Т
4) Не существует таких р, q ^ 0 (pt, q{ ^ 0 н не равны нулю одновременно), что
П
2 Pfiij = Цфц для всех /= 1, .... п.
Когда все эти условия выполнены, скажем, что линейные платежи А индуцируют дилемму заключенного.
2) Рассмотрим теперь игру в нормальной форме G = (Xh ut; i 1, .... п), где Х[открытые интервалы на действительной прямой, а щнепрерывно дифференцируемая функция, задан*
ная на XN. Пусть дан исход x?XN, такой, что Ф0 для всех і = І, ..п.
Скажем, что игра G имеет локальную дилемму заключенного в точке х, если матрица индуцирует дилемму за-
ключенного. Дайте интерпретацию этому определению на основе результатов первой части задачи.
В олигополии с назначением выпусков из примера 4 найдите исходы, в которых возникает локальная дилемма заключенного.
3) В дополнение к предположениям п, 2 будем считать, что п = 2. Докажите, что игра G обладает локальной дилеммой заключенного в х тогда и только тогда, когда справедлива следующая система неравенств:
(16)
= 2},
дщ_ дщ_ \ п дх2 дхг ) ^ ’
где все производные берутся в точке х.
Докажите, что в случае общего положения любая окрестность NE-исхода или исхода, оптимального по Парето, пересекается с областью (16) (дайте точное определение общего положения).
Изобразив графически область (16) для двух моделей олигополии из примера 5, докажите, что область (16) лежит между І?і:-исходами и границей Парето. До какой степени эта конфигурация является общей? Как условие (16) обобщается на случай п 3? Для произвольного целого п?
СМЕШАННЫЕ СТРАТЕГИИ
В некоторых играх в нормальной форме, хотя каждый игрок может выбирать по желанию любой элемент из своего множества стратегий, тем не менее рациональное поведение заключается в добровольной рандомизации собственного выбора. Это порождает известную неопределенность в выборе стратегии игрока и вызывает реакцию остальных, которая может оказаться ему выгодной.
. Рандомизация поведения требует держать в секрете действительно выбранную стратегию (т. е. игроки должны определять стратегии независимо и одновременно). Рандомизация моделирует блеф и отражает идею вездесущности оптимальных стратегий.
Хитрить это значит внушать, что действуешь таким-то образом, или в таком-то месте, в такой-то момент, тогда как в действительности все происходит по-другому. Это, следовательно, своего рода потенциальная вездесущность, как всегда было известно и отмечалось ранними авторами, говорившими о стратегии.
Ксенофонт писал, что знание того, что где-то находится отряд противника без знания его местоположения и сил, разрушает безопасность и все места неизбежно становятся подозрительными (Гильбо [1968]).
Допуская использование смешанных (рандомизированных) стратегий и предполагая, что игроки ориентируются на функции полезности в смысле фон Неймана и Моргенштерна, мы получаем смешанное расширение исходной игры. При этом могут появиться новые равновесные по Нэшу исходы.
Если исходные множества стратегий конечны, то смешанное расширение игры всегда имеет непустое множество равновесий по Нэшу (разд. 2).
Если исходные множества стратегий бесконечны, то возникают определенные топологические трудности. Компактности множеств стратегий и непрерывности функций выигрыша тем не менее оказывается достаточно для того, чтобы гарантировать существование по крайней мере одного NE-исхода (разд.
3).
1. СМЕШАННОЕ РАСШИРЕНИЕ ИГРЫ
Пример 1. Игра де Монмора
В конце 18-го века французский математик Рене де Монмор рассмотрел следующую ситуацию. Для того чтобы сделать подарок своему сыну, отец предлагает: Я возьму золотую монету в правую или левую руку, а ты назовешь одну из них. Если монета у меня в правой руке и твоя догадка правильна, то ты получишь одну золотую монету. Если же монета у меня в левой руке и твоя догадка правильна, то ты получишь две монеты; в противном случае ты не получишь ничего.
Затем Монмор спрашивает, во сколько следует оценить для сына этот подарок, принимая во внимание, что если в этой игре игроки одинаково проницательны и наблюдательны, то нет возможности выработать правило поведения, т. е. не существует оптимальной стратегии в этой игре).
Наша игра 2x2 двух лиц с нулевой суммой такова:
В этой игре нет цены /sup inf и = 0, inf sup и = IV Ни у
одного из игроков нет оптимальной стратегии. Как в любой игре двух лиц с нулевой суммой, не имеющей цены, выяснение, какую стратегию использует противник, позволит добиться хорошего результата за счет использования оптимальных ответов (см. гл.
I, разд. 3). Следовательно, возникает борьба за второй ход, в которой каждый игрок желает скрыть свой окончательный стратегический выбор и в то же время разведать намерения противника.
Но даже глубочайшей секретности недостаточно для того, чтобы не позволить противнику угадать стратегический выбор. Если игрок производит выбор на основе детерминированных дедуктивных рассуждений, то его разумный противник может восстановить саму цепь рассуждений (см. замечание 1 разд.
1 гл. III).
Естественный способ сделать собственный выбор непредсказуемым состоит в том, чтобы сделать его случайным: вместо выбора так называемой чистой стратегии х± из множества {L,R) сын может использовать рандомизированную стратегию рх, выбирающую значения L и R соответственно, с вероятностями ріг 1 pi. Представим себе, например, что сын изготавливает монету, которая с вероятностью рг выпадает на одну сторону, и использует эту монету для выбора своей оптимальной стратегии.
Предположим теперь, что отец не может видеть бросание монеты. Отсюда следует, что стратегия отца, является ли она случайной величиной или нет, не может коррелировать со стратегией сына и, значит, ожидаемый выигрыш, соответствующий так называемой смешанной стратегии р^ не менее inf {2ри
Выбирая рх -j , сын гарантирует себе ожидаемый выигрыш
не менее 2/3. Рассмотрим теперь ситуацию с точки зрения отца. Применяя стратегии L и R соответственно с вероятностями рг, 1р„, он гарантирует себе проигрыш не более величины sup {2ра, 1 Р2}- t
Выбирая р2 = у, отец гарантирует, что ожидаемый проигрыш будет не больше 2/3. Итак, мы заключаем, что внесение тактической неопределенности в стратегический выбор приводит к цене 2/3, которая является разумной оценкой щедрости отца.
Упражнение 1
Используйте аналогичные рассуждения для игры раз дватри (пример 4, гл. I). Докажите, что если игроки используют рандомизированные стратегии, то цена игры равна 6/1 h
Определение 1. Пусть G (X,-, и,.; і ? N) игра в нормальной форме, в которой X,- конечные множества при всех /? Л/.
Смешанной стратегией игрока і называется вероятностное распределение р,- на X,-. Следовательно, множество Mt смешанных стратегий /-го игрока есть единичный симплекс в R*'.
Смешанным расширением игры G называется игра в нормальной форме Gm = (Mf, / g N), где
для всех р € MN ,-(р) = 2 і (х) pf (хг) р2 (хг), .. ., р„ (х„). (1)
хе Xfj
В смешанном расширении Gm игры G стратегия игрока / есть вероятностное распределение р,- на Xt. Под этим подразумевается, что игрок і конструирует собственную лотерею, в которой стратегия х{?Х{ выпадает в соответствии с р,-. То, что лотерея его собственная, означает, что только игрок і знает стратегию х{, которая действительно выпала в лотерее (даже если остальные игроки, возможно, знают вероятностное распределение pf).
Более того, лотерея і'-го игрока стохастически не зависит от лотереи /-го игрока при всех /, /' Ф і (таким образом, игрок / не может получить никакой информации о лотерее t-ro игрока на основе наблюдения своей собственной лотереи).
Поскольку случайные переменные независимы в совокупности, то ы; (р) есть ожидаемый выигрыш игрока і. Принимая и{ за функцию выигрыша игрока і в игре Gm, мы тем самым считаем, что игрок і сравнивает различные лотереи р на р', попросту сопоставляя связанные с ними математические ожидания выигрыша И/ (р) и u-t (р'). Другими словами, и{ есть функция полезности по фон НеймануМоргенштерну, которая распространяет предпочтения игрока і на все возможные лотереи на XN. Дальнейшие обоснования этого предположения относятся к теории статистических решений и здесь не будут рассматриваться (см.
Льюс, Райфа [1957]). Теперь существенно, что функция щ (х) принимает действительные значения, в то время как в предыдущих трех главах важны были только отношения предпочтения, индуцированные функциями ut на Хщ.
Чистая стратегия xt ? X,- игрока і в исходной игре будет отождествляться со смешанной стратегией бxt?Mh выбирающей xt с вероятностью 1:
J 6*, (*[) = 0, х'і^Хі, х'іФх
\6*,(*г)*1.
В самом деле, из формулы (1) сразу следует, что
и1(Ьх) = иі(х) для всех x^XN и bx = (bx.)iiN.
Поэтому будем рассматривать Xt как подмножество Mh а ,- как расширение и{ с XN на MN-
Теорема 1. Если Xtконечное множество для всех i g /V, то множество равновесных по Нэшу исходов в игре Gm является непустым компактным подмножеством множества Мы. Более того, оно содержит множество равновесных по Нэшу исходов в игре G:
W?(G)cW?(GJ^=0. (2)
Доказательство. Выберем любой равновесный по Нэшу исход х в G. Обозначим и заметим, что
sup и, (р„ 6Х) = sup щ (yt, xt),
иееМ( Г ?і^Х{
поскольку Mt выпуклая оболочка Xt (множество Xt отождествлено с подмножеством множества М{) и функция щ линейна по переменной pf.
Теперь в силу того, что исход х есть равновесие по Нэшу, имеем
sup ut (уi, xt) = щ (х) = и{ (Ьх , 8*г).
уі*Хі
Объединяя эти утверждения, получаем, что Ьх есть NE-но ход в игре Gm.
Заметим далее, что игра Gm удовлетворяет предположениям теоремы Нэша (теорема 2, гл. ІИ). А именно, М{ является выпуклым и компактным в RX‘, и{ непрерывна на Мц и линей на относительно переменной р,.
Доказательство теоремы 1 завершено. I
В качестве следствия леммы 1, гл. IV получаем, что все ЛЛЕ-исходы в игре Gm со смешанными стратегиями являются индивидуально рациональными в Gm. На самом деле они также являются индивидуально рациональными в исходной игре G, как показывает следующий результат
Лемма 1. Гарантированный выигрыш игрока і в исходной игре не больше его гарантированного выигрыша в смешанном расширении игрыі
для всех і € N sup inf щ (xt, xt) ^ sup inf ui (py, p,-). m
i(eA( дубМуи(бМ( w
Доказательство. Фиксируем игрока l € V, чистую стратегию xt 6 X; и для каждого / € ?\{і} некоторую смешанную стратегию ру g Му. Тогда щ (6*;, pf) есть математическое ожидание
функции ut{x(, - )g(сужение щ на Xj для фиксированного X.) относительно произведения вероятностных мер ® ру на Хи
/ва?\Ю
Следовательно, имеем
inf щ (xt, xt) й, (6*, р,).
Это неравенство справедливо для всех р, g Mt, поэтому ІШ ut (Xt, Xt) inf Щ фх pt) sup inf щ (py, pi).
*,**1 ^,еМі iiteMt
Поскольку выбор xt произволен, доказательство леммы 1 завершено.
Применяя полученные выше результаты к играм двух лиц с нулевой суммой, сформулируем
Следствие из теоремы 1 и леммы 1. Пусть для данной игры G = (X1( Х2, ых) с нулевой суммой, в которой множества лг, Х2 конечны, игра с нулевой суммой Gm = (M1, Мг, щ) является ее смешанным расширением. Тогда игра Grn имеет по крайней мере одну седловую пару и цену, которую мы назовем ценой игры Gm (или ценой игры в смешанных стратегиях) и обозначим vm(ut).
Более того,
sup inf и1(х1, inf sup (Xj, x2). (4)
JT6 X, x2€ X2 x2€ X2
Предположим сначала, что исходная игра G имеет цену и у каждого игрока имеется оптимальная в игре G стратегия. Тогда смешанное расширение игры G имеет ту же цену и произвольные выпуклые комбинации оптимальных стратегий в игре G являются оптимальными стратегиями игроков в игре Gm (см. задачу 2, п. 1).
Предположим напротив, что игра G не имеет цены и, следовательно, у игроков нет оптимальных стратегий. В игре Gm каждый игрок имеет по крайней мере одну оптимальную смешанную стратегию, и цена игры лежит на отрезке Tsup inf ultL x,
inf sup иЛ. (В общем положении в обеих частях (4) имеют
Хг х, J
место строгие неравенства, см. задачу 1 ниже.) Типичным примером является игра Монмора (пример 1) со смешанной ценой 2/3 и оптимальными осторожными стратегиями обоих игроков
(3-L + -f- R) . См. также разд. 2, в частности упражнения 7, 8.
В качестве еще одной иллюстрации к теореме 1 рассмотрим дилемму заключенного (пример 1 гл. I).
В смешанном расширении этой игры агрессивная стратегия по-прежнему является единственной доминирующей стратегией для каждого игрока, поэтому NE (G) = NE (Gm).
Наш последний пример демонстрирует возможность следующей ситуации:
0 Ф NE (G) cNE (Gm).
Пример 2. Смешанные стратегии в игре перекресток-
В'игре перекресток (пример 2 гл. Ill) имеются два NE-йсхода в чистых стратегиях. В смешанном расширении возни*
кает еще один NE-исход, а именно пара (р*, р*):
где (5)
бі (бц)смешанная стратегия, при которой с вероятностью 1 игрок проезжает перекресток (останавливается).
Имеем
иі Фи Pf) гИТІ* 1 e)=ss 1 ,
t*?)-fex2+dr?xo=i_^.
В силу линейности щ относительно р^получаем i(h- = (р*. р?) для всех
Меняя ролями игроков 1 и 2, в силу симметрии игры получаем и% (Р* Р2) = ы2 (р*, pf) для всех р2?М2.
Отсюда следует, что (р*, \if) NE-исход в смешанном расширении игры перекресток.