РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
Имея возможность координировать свои действия, игроки могут договориться о выборе любого М Е -исхода в чистых стратегиях х*. Это соглашение устойчиво не только по отношению к возможным индивидуальным отклонениям (свойство ME-исходов), но также против отклонений коалиций. В самом деле, предположим, что для каждого участника і из некоторой коалиции Т, Т а. М, оказывается выгодным переключиться со стратегии xf на стратегию xt = 1xf
Ui(xT, xfc)^i Ui(x*) для всех i?T, j
Ц{(хГ, xtc)Ui(x*) по крайней мере для одного І€Т.
Предположим сначала, что число t, определенное формулой
t = 2 хі + 2 xf, равно t*. Тогда по крайней мере для одной іет іетс
пары ja?T выполнено
( х? = 0 лгЛ = 1,
\ *? = 1 Xj, = 0.
Применяя (1) последовательно к /1( /2, получаем
а(/*) ^ Ь(пі*)
I =3a(t*) = b (ni*),
следовательно, щ (xT, х%) = и{ (х*) для всех і € N, что противоречит (1).
Предположим теперь, что t t*. Тогда по крайней мере для одного і € Т имееем
х* = 0, xt = \.
Отсюда в силу (1)
b (п/*) a (t).
Поскольку b (nt*X а (/? + 1), окончательно получаем tt*+l. Полученное противоречие доказывает наше утверждение.
Мы доказали, что любое соглашение, основанное на использовании конкретного М?-исхода, является устойчивым также по отношению к отклонениям коалицией, т. е. любой NE-исход является в данном случае сильным равновесием (см. определение 1 ниже). Если а(і*) и Ь(п1+) достаточно близки, то все игроки в соответствии с соглашением получают приблизительно равные выигрыши, т. е. выбор конкретного WE-исхода не является конфликтной ситуацией. Для реализации одного из этих исходов пираты должны последовательно и открыто выбирать корабль по следующему алгоритму:
*,- = 1 если а(хі + ... +Х;_г + \) b(i[х, + ...+х,._1]), х,- = 0, если Ь (і[х,+ ... +x,_j]) а(х,+ - - +*,-, + !)-
Определение 1. Для данной игры в нормальной форме 0 = (Х/, и,-; і 6 N) скажем, что х*исход сильного равновесия, если не существует коалиции игроков, для которых было бы выгодно отклониться от данного исхода в случае, если дополнительная коалиция не реагирует на отклонение:
?Г с N ?хГ € Хт не выполнено
I ?/^Г u,(xTl xfc) ut (X*),\ 3 І?Т иi (xT, xfc) ut (*?).
Обозначим SE (G) множество сильных равновесий в игре G. Оно может быть пустым.
Полагая T N в формуле (2), получаем, что S?-hcxoa оптимален по Парето. Полагая Т = {і}, і ^ N, получаем, что этот исход является равновесным по Нэшу.
Ясно, что для игр двух лиц SE-исходэто просто оптимальные по Парето й/?-исходы.
Наша интерпретация свойства стабильности (2) основана на двухэтапном процессе принятия решения. На первом этапе игроки приходят к договоренности о некотором конкретном исходе х*. Далее обмен информацией прекращается, и каждый игрок самостоятельно принимает решение о своей окончательной стратегии. Любой игрок і € Л/ может отказаться от использования стратегии xf, но он не может информировать остальных игроков о своем отклонении.
Может также сформироваться любая коалиция Т, отклоняющаяся от хf и выбирающая хг, но игроки вне данной коалиции не могут быть информированы об этом изменении, поэтому ожидается, что они будут придерживаться того поведения, о котором была достигнута договоренность Ur’c). Это ограничение обмена информацией является основным моментом, обосновывающим содержательность определения 1, как показывает от противного приведенный ниже пример 2. См. также определение 1 гл. Ill и следующие за ним комментарии. (Заметим, что для сильных равновесий мы не обсуждаем никаких процедур нащупывания, поскольку близорукое поведение не может быть обосновано при кооперативном способе принятия решений.)
На примере игр двух лиц мы убедились в том, что незыблемость любого ME-исхода разрушается, если возникает борьба за лидерство (см. пример 2 и лемму 2 гл. III).
Аналогичная ситуация возможна и в игре п лиц, что демонстрирует наш следующий пример.
Пример 2. Игра переговоры
п игроков должны поделить доллар. Игроки дают свои заявки арбитру, который удовлетворяет их, если они совместны. В противном случае ни один игрок ничего не получает:
X/ = [0, 1] для всех i?N,
щ (*) =
О, если 2 х/ !-
Мы утверждаем, что
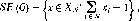
другими словами, исход является сильным равновесием тогда и только тогда, когда соответствующие заявки в сумме дают ровно один доллар. Мы предоставляем читателю проверку этого утверждения.
Заметим, что если коалиция Т, действующая в роли лидера,
выберет некоторый набор стратегий х$ так, что выполнено
условие 2*^=1е (е 0 мало), то коалиция Т, действую-іет
щая как ведомая, выберет в качестве оптимального ответа вектор заявок хтс, такой, чтох, = еи Тс
Следовательно, любой участник или коалиция, присвоив себе право выступать в роли лидера, может забрать почти весь доллар! Поэтому борьба за лидерство в таких переговорах должна быть весьма интенсивной.
Выберем теперь конкретный S?-исход х*, о котором могли бы договориться все игроки, скажем xf = для всех і 6 ЛЛ Для того чтобы сделать это соглашение стабильным, каждый игрок должен решить не обращать никакого внимания на заявки свыше 1/7і со стороны любого игрока, который попытался бы захватить лидерство. Наилучшим образом такая политика глухоты может быть реализована путем разрыва всех каналов обмена информацией между игроками, после чего каждый игрок может изменить свою стратегию, но он не может сделать этого публично.
Решающим моментом, обеспечивающим стабильность соглашения, основанного на конкретном SB-исходе, в рассмотренной игре и аналогичных играх является ограничение обмена информацией между игроками. Это ограничение должно быть законом (как при системе тайного голосования) или физическим ограничением (спутники Одиссея затыкали уши воском). Следовательно, необязательные соглашения требуют некоторых обязательных ограничений в обмене информацией.
Этот момент станет особенно наглядным в концепции равновесия в совместных смешанных стратегиях, которой мы посвятим следующий раздел.
В следующей главе нам потребуются симметричные информационные ограничения для того, чтобы использовать взаимные предостерегающие угрозы как механизм кооперации (см. гл. VI).
Мы уже знаем (гл. Ill, разд. 2), что игра в нормальной форме, у которой множества стратегий являются открытыми подмножествами евклидовых пространств, а функции выигрыша дифференцируемы, в случае общего положения не имеет оптимальных по Парето Л/?-исходов и тем более SB-исходов.
Однако при некоторых очень сильных предположениях о выпуклости существование SE-исхода может быть гарантировано (см. Ауман [1959]).
Упражнение 2. Обобщение примера t
Каждый игрок должен выбрать одно из р общественных благ. Если tkобщее число игроков, выбравших благо с номером k, k=\, ..., р, тогда каждый из tk потребителей получает выигрыш ak(tk), где ак(-) есть неудовлетворение при потреблении блага k, причем это строго возрастающая функция от tk.
Следовательно, получаем игру
X,- = {1, ..., р}, i ?N,
Ui = ak((k), если xs = k и tk = \{i ?N\x; = k}\.
Предположим, что ак(0) = 0 и ак{п)= 1, 6=1, ..., р. Докажите существование по крайней мере одного сильного равновесия в данной игре и приведите условия, при которых все 5Е-исходы приводят к одному и тому же распределению(/j, - - - , tp).
Упражнение 3. Игра размещение магазинов с дополняющими товарами
Два владельца магазинов решают разместить свои магазины на одной улице (на отрезке [0, 1]). Они предлагают дополняющие товары (как, скажем, магазин спортивного оборудования и бюро туристических путешествий), а потому успехи одного оказывают положительное влияние на другого (в противоположность примеру 5 гл.
IV). Кроме того, игрок 1 желает разместить магазин как можно ближе к точке 0, а игрок 2 как можно дальше от точки 0. Таким образом, получается следующая игра:
( х1 = х2 = [0, 1],
I щ{хх, л:2) = а]дг1 I хх х21,
I ut(xv хг) = а2\хг 11 \хх х2\,
[ где ccj 0 а2.
Предположим, что а(^1, 1 = 1, 2.
Докажите, что исход (xlt х2) является сильным равновесием в этой игре тогда и только тогда, когда хх = х%. Разберите остальные случаи,
2. РАВНОВЕСИЕ В СОВМЕСТНЫХ СМЕШАННЫХ СТРАТЕГИЯХ
Смешанные стратегии дают новые равновесные по Нэшу исходы (по теореме 1 гл. IV каждая конечная игра имеет по крайней мере один NE-исход).
С кооперативной точки зрения равновесие по Нэшу в смешанных стратегиях есть необязательное соглашение, которое обеспечивается тайностью проведения лотерей, организуемых игроками для случайного выбора окончательного решения (т. е. чистой стратегии).
Пример 3. Вежливые водители
Модифицируем выигрыши в игре перекресток (пример 1 гл. Ill): если один водитель остановился, то для него предпочтительнее, чтобы другой проехал.
(Этот пример известен в литературе под названием семейный спор, см. Льюс и Райфа [1957].)
В дополнение к двум чистым NE-исходам с векторами выигрышей (l-f-e, 2) и (2, 1+е) соответственно эта игра 2x2 имеет вполне смешанное равновесие, а именно
- j. Этот0+1-с вектором выигрышенсмешанный2 + 8’ ' 2+8j
??-исход доминируется по Парето (любым чистым ??-исходом), поэтому его можно обосновать только тем, что он приносит одинаковые выигрыши идентичным игрокам и в этом смысле является справедливым. Однако в этом смешанном ?/Г-исходе
каждый игрок получает выигрыш 1 +2+і ’ Равный гарантированному выигрышу в смешанных стратегиях. Вместе с тем стратегии р* образующие ?іГ-исход, не являются осторожными, а потому не гарантируют игроку этого выигрыша.
Для проверки этого утверждения заметьте, что цена игры
(Лх, Хг, ut) в смешанных стратегиях равна 1+ггт- и единст-
*4-8
венная седловая пара есть (р, р*), где
бц.
Более того,Ml** бц)=-^-1+2^ = i(pf, pf) = M,(^ бц),
откуда ясно, что смешанная N?-стратегия pf’ является более рискованной, чем осторожная стратегия pj. Единственным стратегическим аргументом в пользу равновесия в смешанных стратегиях можно считать свойство стабильности. Если игроки могут тайно проводить лотереи, то необязательное соглашение о реализации вполне смешанного ?-исхода является стабильным.
Следовательно, для каждого игрока действия остальных вполне предопределены. С этой точки зрения аргументация в пользу осторожных стратегий обманчива, поскольку применение осторожных смешанных стратегий индуцирует последовательность наилучших ответов, что делает окончательный исход совершенно непредсказуемым.
С одной стороны, смешанный ?-исход является разумным, если игрок считает своего партнера столь же рациональным, как и он сам, хотя Л/?-стратегия является более рискованной, чем осторожная стратегия, если партнер может сыграть глупо. С другой стороны, осторожная смешанная стратегия выбирается из соображений минимума риска и, следовательно, безопасна, насколько это возможно.
Тем не менее у рационального игрока возникает желание одностороннего отклонения от исхода, состоящего из пары смешанных осторожных стратегий, поскольку такое отклонение увеличивает выигрыш. Возвращаясь к игре перекресток, построим теперь случайный механизм, который не сводится к независимой рандомизации стратегий, причем этот механизм позволит сделать рановесный исход оптимальным по Парето.
Пример 3'. Игра перекресток со светофором
Игроки сооружают специальный случайный датчик, который показывает (зеленый, красный) и (красный, зеленый) с равной вероятностью. Соглашение состоит в том, что на зеленый свет следует проезжать без остановки, а на красныйостанавливаться.
Это соглашение является стабильным, поскольку при каждом исходе лотереи получается равновесие по Нэшу. Результирующее математическое ожидание выигрыша равно -- + --для каждого игрока, тем самым обеспечивается оптимальность по Парето и справедливость.
Определение 2 (Ауман [1974])
Для игры G = (X(-, и,.; i?N) с конечными множествами стратегии обозначим через L = (L(x))xexN совместную лотерею, т. е. вероятностное распределение на XN. Для всех i g N и для всех X/ € Kt обозначим через LX( условную вероятность реализации х^Хн^у).
_1_
2 у
Vl eXN\{i)
0,
L(xh xt), если знаменатель не равен нулю,
если L (xit уг) = 0 для всех у,?ХN\{i].
Скажем, что L есть равновесие в совместных смешанных стратегиях в игре G, если выполнены следующие неравенства:
Vt g N, ?х0 уi ? X; 2 Щ (xh xt) LX[ (xt)
*:eXN\U)
2 Щ(Уі. x,)LX{(xt). (3)
X!SXN\{C)
Обозначим через CE (G) множество всех равновесий в совместных смешанных стратегиях в игре G.
Кооперативный сценарий, служащий обоснованием определения 2, состоит в следующем. Игроки совместно сооружают случайный датчик, который может производить выбор исходов х ? XN с вероятностью L (х). Если реализовался исход х, то игрок і получает информацию только о компоненте х{.
Далее каждый игрок выбирает свободно и независимо, а также тайно свою настоящую стратегию. Сигнал xt воспринимается игроком і как необязательное предложение сыграть х{. Условия (3) означают, что выполнение соглашения о выборе х{ игроком і обеспечено автоматически при той ограниченной информации, которая доступна каждому игроку.
В самом деле, пусть участнику і предложено использовать стратегию xt. Он выводит из общего распределения L, что с вероятностью Lx. (xf) набор xt будет выбран. Следовательно,
[иі (Уі - ). Ц] = 2 иі(уі, xt)Lx.(xt)
XlSXN\{i)
есть математическое ожидание его выигрыша при применении стратегии у{ € Х{, если все остальные игроки согласны в выборе стратегий следовать сигналу. Таким образом, условие (3) означает, что использование стратегии, предложенной датчиком, есть оптимальный ответ игрока і при заданном уровне инфор-мированности в предположении, что все остальные игроки подчиняются сигналу.
Предположим, что стратегия х{ такова, что L(xt, *f) = 0 для всех xt € т. e. вероятность того, что стратегия х.
будет предложена датчиком, равна нулю. Для такой стратегии х; условие (3) выполняется тривиально, следовательно, мы можем переписать систему (3) в эквивалентном виде
Vi g N Vxit У;Х{ 2 *,) L (xt, x.)
XteXN\{t)
2 U (уi, x,)L(xit X,). (4)
X ... г N\ {i}
Отсюда следует, что лотерея L является равновесием в совместных смешанных стратегиях тогда и только тогда, когда она удовлетворяет системе линейных неравенств (4). Эта система всегда имеет решение, как показывает следующий результат.
Лемма 1. 1) Множество СЕ (G) равновесий в совместных смешанных стратегиях в игре G является непустым выпуклым компактным подмножеством единичного симплекса в R.xw.
3) Если [А = (р,-), 6 n является исходом смешанного ра шире-ния игры G, т. е. исходом игры Gm, то определяемая по этому исходу лотерея L= 0 р.
се/?
L (х) = 0 (X) (5)
(6 N
есть равновесие в совместных смешанных стратегиях в игре G тогда и только тогда, когда уситуация равновесия по Нэшу в игре Gm
Доказательство. Пусть р = (р,-)гл/ исход игры G„ и L соответствующее произведение лотерей, заданное равенством (5). Тогда система (4) примет вид
М*і)-і(6? И,) Р,- (*- ) иі (§? Pf) Для всех і, Х(, Уі. (6)
Это неравенство очевидно, если р; (*,- ) = 0. Следовательно, система (6) эквивалентна системе
Щ(ЬХ., рг) и,-(8У., р?) для всех i%N, х,€[р;1, Уі?Хі- (7)
Предположим теперь, что рсмешанный jVf-исход в игре G. Тогда по теореме 2 гл. IV система условий (7) выполнена. Обратно, из (7) следует, что ы; (6*., pf) не зависит от х{ g [р,]
и, следовательно, равно и, (р). Это завершает доказательство второго утверждения леммы 1.
Далее из теоремы Нэша (теорема 1 гл. IV) следует, что множество NE(Gm) не пусто, откуда получаем непустоту множества СЕ (Gm).
Выпуклость и компактность последнего множества следует из приведенного выше замечания о том, что СЕ (Gm) определяется системой нестрогих линейных неравенств. I
Рассуждения, которые обосновывают стабильность соглашения, базирующегося на равновесии в совместных смешанных стратегиях, во многом аналогичны кооперативному подходу к равновесию по Нэшу. В самом деле, согласно лемме 1 NE-исход как в исходной игре, так и в ее смешанном расширении, отождествляется с равновесием L в совместных смешанных стратегиях, где вероятностное распределение L есть набор независимых случайных индивидуальных стратегий.
В этом случае нет никакой корреляции стратегий различных игроков.
Первый наиболее простой путь получения преимуществ от корреляции индивидуальных стратегий состоит в том, чтобы брать выпуклые комбинации Л?Г-исходов. При этом получается лотерея L типа
р р
L 2 КЬха, 2 ^а = 1. для всех а, (8)
а=І а=1
где Ьжлотерея, в которой исход х выбирается с вероятностью 1, а ХаУ?Е-исход в игре G. Такая лотерея является равновесием в совместных смешанных стратегиях в игре G (заметим, что выпуклая комбинация смешанных NE-исходов также содержится в СЕ (Gm)). Светофор (пример 3') служит примером такого СЕ-исхода. Во многих играх, однако, множество исходов равновесий в совместных смешанных стратегиях шире, чем выпуклая оболочка равновесий по Нэшу.
Это показано в следующем примере.
Пример 4. Музыкальные стулья
Предлагается нестандартная версия игры музыкальные стулья. Имеются два игрока и три стула, помеченные цифрами I, II, III. Стратегия игрока состоит в выборе стула.
Оба игрока несут потери при выборе одного и того же стула. Если же их выборы различны, то тот игрок, скажем і, чей стул сразу следует за стулом игрока /, выигрывает вдвое больше, чем игрок / (предполагается, что I следует за III). Итак, возникает биматричная игра:
В исходной игре нет равновесий по Нэшу. Единственное вполне смешанное равновесие по Нэшу таково:
^ = ^ = Т6і+Тбп+Тбш-
Этот симметричный исход приносит каждому игроку выигрыш, равный единице, и доминируем по Парето. Причина этого в том, что в смешанном исходе (pf, р*) плохой детерминированный исход (і, і) реализуется с вероятностью 1/3. Рассмотрим следующую лотерею L на ХгхХг:
Цх„х%) = ІІ’ *"*.**.- ^ 0, если хх=*хг
Утверждается, что L есть равновесие в совместных смешанных стратегиях в игре (9). Предположим, например, что реализовался детерминированный исход (2, 3) и, следовательно, игроку 1 предлагается использовать стратегию II. При данном L игрок 1 может вывести, что игроку 2 предложено использовать одну из стратегий I или III с одинаковой вероятностью 1/2.
Другими словами, предполагая, что игрок 2 согласен выбирать стратегию, поступающую с датчика, игрок 1 тем самым считает, что игрок 2 использует смешанную стратегию \ б, + ~ бш. Наилучший ответ на эту стратегию и есть стратегия II, поскольку
И] (б[ Ра) Y- 1 Иг) 1 ^ fi2) ~ -
Аналогично игрок 2, которому поступает сигнал применять стратегию III, выводит, что игроку 1 предлагается выбрать стратегию I с вероятностью 1/2 или стратегию II с вероятностью 1/2. В этом случае стратегия 3 является наилучшим ответом игрока 2 на смешанную стратегию р, =у6, + --6И игрока 1.
В силу симметричности нашей игры мы получаем свойство стабильности (3) лотереи L при любых допустимых реализациях.
Заметим, что лотерея L приводит к оптимальным по Парето и справедливым выигрышам (3/2, 3/2), что побуждает игроков вступать в кооперацию на основе использования совместных смешанных стратегий.
Основной чертой необязательного соглашения применять стратегии, вырабатываемые датчиком L, является распределение информации. Оба игрока информированы о лотерее L, которую они выбрали по кооперативному согласию, тем не менее, после того как исход х реализовался как результат применения лотереи, игрок і получает информацию только об t-й компоненте xt. Он не может наблюдать сигнал х{, полученный другим игроком /, а может только вывести из распределения L, что вероятностное распределение х. есть Lx..
Конечно, если L принимает вид (8) при (Х;)аф(Х{)а, для всех і, афа', т. е. распределение L сосредоточено в точках ха, то сигнала xL а достаточно для игрока /, чтобы в точности выяснить сигналы, посылаемые остальным игрокам. В этом случае свойство стабильности (3) требует, чтобы каждый исход был NE-исходом в первоначальной игре (см пример 3').
Пример с музыкальными стульями объясняет, каким образом разумное ограничение возможностей обмена информацией оказывается выгодным с кооперативной точки зрения.
Замечание I
Естественным обобщением определения 2 является рассмотрение возможных отклонений любой коалиции Т с использованием при этом совместной смешанной стратегии L'T на Хт и распространение свойства сильного равновесия на данный рандомизированный случай. Это привело бы к понятию сильного равновесия в совместных смешанных стратегиях, для которого тем не менее нельзя ожидать получения общих условий существования: см., например, игру двух лиц из примера 5 ниже, в которой ни одно равновесие в совместных смешанных стратегиях не является оптимальным по Парето.
В следующем примере в качестве равновесия в совместных вмешанных сратегиях нельзя получить ничего, кроме единственного равновесия по Нэшу. Тем не менее будет приведен новый механизм кооперации, который является более обязательной формой стабильного соглашения, основанного на совместных смешанных стратегиях, и который позволит улучшить по Парето NE-исход.
Пример 5. Конкуренция со специализацией
Два дуополиста снабжают рынок одним товаром, но разного качества. Игра является симметричной. Каждая фирма может выбрать одну из трех стратегий: низкое (L), среднее (УИ), высокое (Я) качество.
Если оба поставят товар низкого качества или обавысокого, то каждый получает нулевую прибыль. Если один игрок выбирает среднее качество, а другой высокое или низкое, то игрок, предложивший среднее качество, получает прибыль 2. Если оба товара среднего качества, прибыль обоих игроков равна 1. Для получения максимальной суммарной прибыли одна фирма должна предложить высокое качество, а другая низкое, при этом игрок, предложивший высокое качество, получает 3, а предложивший низкое качество получает 1.
Заметим, что эта модель может интерпретироваться как известная игра размещение отелей.
Для игроков, придерживающихся некооперативного поведения, эта игра разрешима по доминированию: сначала выбрасываются стратегии L, затем Я. Таким образом, (УИ, УИ) является (единственным1)) NЕ-исходом как самой игры, так и ее смешанного расширения.
Эта игра также имеет единственное равновесие в совместных смешанных стратегиях, которое реализуется на лотерее, выбирающей (М, М) с вероятностью 1 (для проверки этого утверждения заметьте, что С?-лотерея приписывает нулевой вес любой строго доминируемой стратегии, и затем примените это замечание дважды).
Тем не менее оптимальный по Парето выигрыш (2, 2) может быть получен в результате следующего соглашения. Построим лотерею с вероятностным распределением
L = 7Г ®(Н. L) + у 6(L, Я)-
Каждый игрок независимо и тайно выбирает и посылает нейтральному арбитру, который выбран обоими игроками, обязательный сигнал s;, принимающий одно из четырех значений для каждого игрока: три чистых стратегии и сигнал ОВ (согласно лотерее). Получив пару сообщений (s1( s2), арбитр определяет случайный исход (хх, х2) в соответствии с лотереей L. Финальный исход игры определяется по следующему правилу (за этим следит арбитр):
(хи х2), если sx = s2 = OB,
(xlt s2), если s1 = OB, s2 L, M, Я,
1 (si хг)г если si = ^ M, H, s2 = OB,
(sj, s2), если si L, M, H, i 1, 2.
Другими словами, сообщение OB является обязательством применять стратегию, выпавшую по лотерее, причем это обязательство принимается до проведения лотереи.