РАВНОВЕСИЕ ПО НЭШУ
Старший пират никакого участия в дальнейшем дележе не принимает. Если новый дележ отвергается большинством голосов, то предложивший его пират устраняется от дальнейшего участия в дележе, и процедура повторяется для (п 2) пиратов.
Примем достаточно реалистичное предположение о том, что каждый пират знает функции выигрыша остальных. А именно, каждый пират из двух данных дележей предпочитает тот, в котором его доля золотых слитков больше (дележи, дающие ему одинаковую долю добычи, являются равноприемлемыми независимо от долей остальных игроков).
Дух всеобщего недоверия, царивший, как известно, среди флибустьеров, позволяет предсказать, что их поведение будет некооперативным, а тогда остается только найти окончательный дележ.
Вычислим сложное поведение пиратов. Если осталось только два пирата, то старший из них забирает всю добычу, поскольку младший пират не составляет абсолютного большинства.
Пред-ііоложим, что осталось три пирата. Тогда старший из них может предложить дележ, дающий 99 слитков ему и 1 слиток младшему пирату.
Младший пират вынужден согласиться с таким предложением, поскольку он понимает, что оставшись один на один со средним пиратом, он не получит ничего.
Если пиратов четверо (4, 3, 2, 1), то старший из них (4) будет рассуждать следующим образом: Если мое предложение будет отвергнуто, то три оставшихся пирата поделят добычу так: (99, 0, 1) (см. рассуждения выше). Следовательно, я должен предложить такой дележ, который хотя бы одному из них был
выгоднее этого, а мне давал наибольшую возможную долю. Единственным решением этой задачи является дележ (99, 0, 1, 0), в котором старший пират (4) жертвует всего лишь одним слитком в пользу пирата 2.
Равновесный дележ для произвольного количества пиратов может теперь быть найден по индукции. Выше (с.
63) приведены соответствующие результаты в зависимости от общего числа пиратов.
Итак, если /г = 2р+1 или /г = 2р + 2, то в дележе, соответствующем сложному равновесию, доля старшего пирата равна (100 р) слитков. По одному слитку получают р пиратов, которые имеют номера той же четности, что и старший пират.
Парадоксальность этой процедуры дележа состоит в том, что с виду она весьма демократична, однако добыча делится отнюдь не поровну!
Причина этого парадокса в том, что при последовательном исключении доминируемых стратегий не остается никакой возможности для кооперации. Рассмотрим случай трех пиратов.
Среднему пирату следовало бы поспешить предложить младшему некоторый договор (например, о дележе (50, 50)), чтобы провалить предложение старшего пирата (99, 0, 1). Однако откуда у младшего пирата возьмется уверенность в том, что средний пират, став старейшиной, не отнимет у него всю добычу?
Ведь именно такое поведение вытекает из стремления к максимизации выигрыша.
Другими словами, предложение дележа (50, 50) является для среднего пирата доминируемой стратегией.
Задача 5. Переговоры двух лиц при наличии дисконтирую-щего фактора (Бинмор [1980])
Два игрока договариваются по поводу выбора вектора выигрышей из множества Л с: IR+, которое имеет вид
Л = {(г„ г2) 10 г2 ? (гх), 0гх},
Где ?дифференцируемая на [0, 1] функция, причем
при всех t, 0 t ^ 1.
? (1) = 0, ?'(00 ? (0) = 1, ? (t) 0
Процедура та же, что и в примере 5: на шаге 1 игрок I предлагает исход х3^А. Если игрок II отклоняет х1, то он может предложить х2^6-А, где 6, 0 6 I, есть дисконтирующий фактор. Если игрок I отклоняет хг, то он может предложить х3 ? 62 - А и т. д. Если соглашение наступило на шаге t, то выигрыши игроков в игре суть координаты х*.
Если соглашение не достигнуто ни на одном шаге, то выигрыши равны нулю.
1) Докажите, что исход сложного равновесия соответствует достижению соглашения на шаге 1 и сводится к принятию некоторого оптимального по Парето вектора л:(б) из А. Охарактеризуйте л: (б), используя функцию ?.
2) Докажите, что при б, стремящемся к 1, хг (б) уменьшается, а лга (б) возрастает. Докажите, что предельный исход л;(1) есть арбитражное решение по Нэшу на множестве А, т. е. решение следующей задачи: maxzjz3.
ге А
Задача 6. Общественный механизм принятия решений с побочными платежами (Мулен [1981])
Сообщество N = {1, 2, ..., п} должно принять одно решение из конечного множества А = {а, Ь, с, ...}. Есть один частный товар (деньги), который позволяет осуществлять побочные платежи, а полезность каждого игрока квазилинейна (как в задаче 4 гл.
I). Исходная полезность і-го игрока описывается вектором и{ g Если сообществом принято решение а и игрок і получает денежный платеж tt (он может быть как положительным, так и отрицательным), то окончательно полезность для него описывается величиной
u{(a)-j-t(.
Решение (a; t) состоит из общественного выбора a g А и вектора і = (tu tn) денежных платежей, таких, что
и н* и + - - - +tnО-
Обозначим через ® с Л х R" множество всех таких решений.
1) Мы будем рассматривать два различных механизма. В первом из них игроки последовательно предлагают решения, которые должны быть единогласно утверждены остальными.
Игрок, чье решение отвергнуто, теряет в дальнейшем право вето, и денежный платеж ему больше не выплачивается.
Более точно:
Игрок 1 предлагает сначала решение йх (a1, Р) g 3 для единогласного утверждения остальными участниками. Если каждый из игроков 2, ..., п принимает d1, то это и есть окончательное решение. Если по крайней мере один игрок отклоняет d1, то тогда игрок 2 должен предложить решение dz = (a3, Р) g SD с единственным ограничением: t\ 0.
Решение d2 представляется для единогласного утверждения игроками {3, ..., п}. Если оно отвергается хотя бы одним из этих игроков, то тогда игрок 3 будет предлагать d8 = (а8, Р) ? 3), такое, что t\=t\ = 0, и теперь d3 будет представлено на единогласное утверждение игроков {4, 5, ..., п} и т. д. Если предложения игроков 1, 2 ..., (/г2) последовательно отклоняются, тогда игрок (п1) предлагает dn~1 = (an~1, іп~х), где tn~?
имеет видіп~г (0.....О, іп:\, /Г1)-
Только игрок п имеет право отвергнуть dn~x, и в этом случае он выбирает окончательное решение dn = (an, 0).
Докажите, что предложенный выше механизм определяет разрешимую по доминированию игру (при некоторых дополнительных предположениях, аналогичных принятым в задаче 3).
Вычислите выигрыши, соответствующие сложному равновесию. Любое ли сложное равновесие оптимально по Парето?
2) В нашем втором механизме априори задано некоторое начальное решение (а, I). Приведенная ниже процедура символизирует аукцион за право лидерства:
i) каждый игрок назначает %^0 денег как цену за то, чтобы стать лидером;
ii) один из игроков, предложивший наибольшую цену (например, тот, который имеет наименьший порядковый номер), становится лидером. Пусть это игрок t0;
iii) лидирующий игрок і0 платит каждому из остальных н предлагает решение (a; t)\
і?) это предложение ставится на голосование среди остальных игроков. Следовательно, на шаге (і?):
или предложение игрока і0 (а; () поддерживается всеми остальными игроками, и тогда окончательное решение есть (a; t + s), где
Или (по крайней мере) один игрок отвергает предложение игрока і0 и в этом случае принимается начальное решение (іа?, t). Учитывая денежные платежи, получаем окончательное решение (а, /-М).
Проанализируйте игру, получающуюся из данного механизма на основе каких-либо функций полезности. Рассмотрите сначала игру G(t0), начинающуюся с шага ііі), после того как определен лидирующий игрок і0.
Докажите, что игра G (і0) разрешима по доминированию и найдите выигрыши сложного равновесия. Возвращаясь к шагу і), докажите, что вся игра не разрешима по доминированию, но что после соответствующего исключения доминируемых стратегий, получается несущественная игра (см пример 5).
Вычислите соответствующие равновесные выигрыши.
РАВНОВЕСИЕ ПО НЭШУ
Доминирующая стратегия, осторожное и сложное поведение могут быть определены игроками независимо друг от друга. Каждый игрок самостоятельно, зная только нормальную форму игры, может вычислить стратегию (или стратегии), рекомендованную тем или иным принципом рациональности.
Синхронность стратегических выборов в этом случае не требуется.
В противоположность этому равновесие по Нэшу может быть обосновано только динамическим сценарием, в котором стратегические решения, принимаемые сегодня, зависят от предыдущих партий игры или хотя бы от начальной позиции. Таким образом, теперь уже общение игроков становится неизбежным.
Они должны хотя бы наблюдать одни и те же прошлые исходы игры. Приведем определение и обсудим концепцию равновесия по Нэшу прежде, чем подробно исследовать ее привлекательные математические свойства (существование и устойчивость).
1. ОПРЕДЕЛЕНИЕ И ОБСУЖДЕНИЕ
Для данной игры в нормальной форме предположим, что игроки ведут себя так, как будто они не знают о своей стратегической взаимозависимости: когда игрок і рассматривает переключение со стратегии xt на стратегию у{, он не учитывает реакции на свой ход остальных игроков, т. е. он ожидает, что остальные не изменят своей стратегии в ответ на его изменение. Это предположение правдоподобно, если игроков так много, что воздействие, производимое на общий исход одним отклонением, незначительно (см. пример 1). Альтернативная интерпретация предполагает полное незнание игроком і функций выигрыша Uj при / € N\{i}. Игрок і может добывать информацию о функциях Uj, наблюдая реакции игроков из N\{i} на использование им стратегии, выгодной в предположении, что никакой реакции остальных не последует (эта линия рассуждений развивается в разд.
3).
Определение 1. Пусть дана игра в нормальной форме G = (X,-, щ\ i g N). Скажем, что исход x (x;)ieN есть равновесие по Нэшу (кратко NE-нсхоц) игры G, если
?/г€^г иіІУі *-)/(*,- . xt). (1)
Обозначим через ME(G) множество равновесий по Нэшу в игре G.
В равновесии по Нэшу х игрок і рассматривает стратегии Xt как экзогенно заданные и максимизирует функцию м,- на множестве своих стратегий у{. Свойство (1) равновесия по Нэшу состоит в том, что х{это один из наилучших ответов на стратегии xt.
Концепция равновесия по Нэшу не дает конкретных рекомендаций по выбору стратегии, как это было в случае сложного или осторожного поведения. Обычно, если в игре есть два невзаимозаменяемых і??-исхода (см. пример 2 и лемму 2 ниже), то игроки не могут выбрать стратегии, порождающие равновесие по Нэшу, без некоторого механизма координации (на этот счет' см. также гл. V, разд. 2).
Заметим однако, что в играх двух лиц с нулевой суммой Л^Е-исходы суть просто седловые точки (определение 6 гл. I), поэтому ?-стратегии совпадают с осторожными оптимальными стратегиями (теорема 3 ?л.
I).
Представим себе два крайних сценария, мотивирующих Концепцию равновесия по Нэшу:
1) С нормативной точки зрения, предположим, что игроки сообща обсуждают, какой выбрать исход, пока не договариваются до необязательного соглашения. В следующий момент они расходятся, и всякий обмен информацией между ними становится невозможным. Затем каждый игрок тайно выбирает свою настоящую стратегию, не зная действительные стратегические выборы остальных.
Игрок может быть верен достигнутому соглашению, а может и отступить от него, не платя при этом штрафа, и использовать любую, угодную ему стратегию. Тогда (и только тогда), когда согласованный исход есть равновесие по Нэшу получаем стабильное соглашение: Предполагая, что Все остальные лояльны, я тоже лучше буду лоялен (чем более бесспорна моя добродетель, тем больше побудительных мотивов Я дам остальным к тому, чтобы и им быть добродетельными). Этот полукооперативный сценарий исследован в гл.
V как особый способ кооперации: концепция равновесия по Нэшу связана как с некооперативной, так и с кооперативной частью teopHH.
2) С описательной стороны мы ищем устойчивые исходы близоруких процедур нащупывания), в которых каждый игрок придерживается оптимальной стратегии при (постоянно нарушаемом) условии, что остальные не меняют своих стратегий. Когда эта процедура нащупывания по Курно (см. ниже разд.
3) сходится, мы получаем равновесный по Нэшу исход.
Замечание: Метатеоретические соображения, предложенные фон Нейманом и Моргенштерном, дают альтернативный подход к нормативному обоснованию Х?-исходов. Рассмотрим случай полной информации и предположим, что некоторая теория рекомендует в игре G для каждого игрока і оптимальную стратегию Х{.
Поскольку каждый разумный и полностью информированный игрок может сам восстановить всю теоретическую аргументацию и вычислить рекомендованный исход, то необходимо, чтобы наша теория предлагала NE-исход если мы хотим, чтобы эгоистичные игроки, максимизирующие свои функций выигрыша, действительно прислушивались к рекомендациям теории.
Пример 1. Двоичный выбор с взаимным влиянием (Шеллинг [І979])
Пусть имеется много идентичных игроков. Каждый из них должен выбрать одну из двух стратегий: 0 или 1 (скажем, для определенности, использовать собственный автомобиль или общественный транспорт).
Если і(, доля игроков, использующих стратегию
1 (общественный транспорт), то числа a(t) и b(t) обозначают соответственно выигрыши любого игрока, использующего стратегию 1 и стратегию 0 (собственный автомобиль). Таким образом, получается следующая игра в нормальной форме:
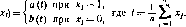
Предположим, что а и b такие, как на рис. 1.
Это означает, что если доля игроков, использующих общественный транспорт, больше то уличное движение настолько свободное, что водитель автомобиля счастливее, чем пассажиры автобуса (учитывая агрегированный показатель затрат и комфорта). Если же доля автомобилистов больше, чем (1 t0), то движение настолько интенсивное (возможно с некоторым приоритетом в правилах для автобусов), что сравнение теперь в пользу пассажиров автобусов. В этой игре равновесиями по
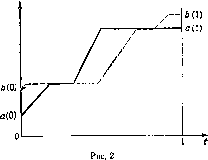
Нэшу являются исходы х*, для которых выполнено условие
П
где t* ~ ^ xf, і = і
означающее, что для каждого отдельно взятого игрока обе допустимые стратегии равноценны.
Пусть величина б обозначает долю игроков, решивших пе-
Гключиться со стратегии 0 на стратегию 1. Заметим, что если настолько велико, что b(t) = a(t) а{і + 6), то выигрыши этих игроков увеличатся при переключении, если бтратегии остальных игроков останутся прежними.
Однако если это переключение произойдет, то у игроков возникнет желание переключиться со стратегии 1 на стратегию 0, поскольку выполнено условие а (t -{- б) b (t -Ь б). Если
П
то желание осуществится, то доля У, х, уменьшится и вновь вернется на отрезок [70, fj.
Аналогично, пусть бдоля игроков, переключившихся по каким-либо причинам (например, из-за случайных ошибок) со стратегии І.на стратегию 0, причем tб /0.
Тогда в силу условия b(tb) a (tб) у игроков появится Желание переключиться обратно на стратегию 1. При овущест-
П
влении этого желания доля х, увеличится и вновь вернется
/-1
йа отрезок [/„, J.
Упражнение 1
Рассмотрим два различных варианта пары функций а (- )(’)-
1) Предположим, что обе функции а и b возрастают по t и a(t) ? (і) для всех t € [0, 1]. Докажите, что соответствующая игра является обобщением дилеммы заключенного (пример 1 гл.
I), в которой единственное равновесие по Нэшу является также равновесием в доминирующих стратегиях.
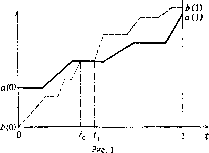
2) Предположим, что а и b такие, как на рис. 2. Докажите, что соответствующая игра имеет 3 типа і?Е-исходов, один из которых не устойчив по отношению к рассмотренным выше 6-отклонениям.
Отложим до разд. 3 формальный анализ процедуры нащупывания по Курно, который является важным этапом на пути некооперативной интерпретации равновесия по Нэшу.
Определение 2. Исход х игры G = (X{, up, i g N) называется индивидуально рациональным, если
sup inf и{ (уі, г/г) = at и{ (х) для всех і € N.
Уі6 Х( i/;€ Xj
Лемма 1. Все NE-исходы индивидуально рациональны).
Доказательство. Из (1) получаем, что для всех і справедливо неравенство
?/г€*г inf ut(yh уЬЩ(Уі, хг)иг(х).
!/; X/
Взяв супремум по у( в этих неравенствах, получаем (2).
С одной стороны, NE-исход дает каждому игроку по крайней мере его гарантированный выигрыш (индивидуальная рациональность), хотя NE-стратегия может и не быть осторожной (см. пример 2). С другой стороны, NE-исход может не быть оптимальным по Парето (как в примере 1, рассмотренном выше). §олее того, если каждый NE-исход оптимален по Парето, то сосуществование нескольких различных оптимальных по Парето МЕ-исходов порождает обычно борьбу за лидерство (гл. II, разд. 4), что убивает всякую надежду найти оптимальные стратегии.
Это обстоятельство иллюстрируется следующим примером.
Пример 2. Игра перекресток
Два автомобилиста движутся по двум перпендикулярным дорогам и одновременно встречаются на перекрестке. Каждый из них может остановиться или ехать. Следующая игра 2x2 формализует данную ситуацию в предположении, что каждыйигрок предпочитает остановиться, чем пострадать в аварии (исход (ехать, ехать)), и проехать, если другой сделал остановку.
Неотрицательное число е соответствует неудовольствию от созерцания проехавшего, в то время как сам ты вежливо остановился; величина е определяется этическими нормами общества.
Оба AfE-исхода (а именно, (остановиться, ехать) и (ехать, остановиться)) оптимальны по Парето. Тем не менее они не взаимозаменяемы.
Для каждого игрока оптимальной стратегией является остановка, если другой игрок решил проехать перекресток, и наоборот, выгодно проехать, если другой игрок остановился. Высказав решимость придерживаться неосторожной стратегии ехать, игрок выигрывает, поскольку он заставляет другого остановиться и, следовательно, получает максимальный выигрыш, равный 2. Поскольку ни один исход не дает обоим игрокам выигрыш, равный 2, то неизбежна борьба за лидерство.
Каждый игрок будет изображать, что он утратил способность переключиться со стратегии ехать на стратегию остановиться (например, прикидываясь пьяным), и в то же время внимательно наблюдать за своим противником, чтобы выяснить, а вдруг тот и в самом деле не сможет остановиться. Поразительно, что наиболее выгодным оказывается нарочито нерациональное поведение, которое тем самым оказывается вполне разумным.
Симметричность ролей обоих игроков делает невозможным нахождение' арбитражного решения борьбы за лидерство на основе нормальной формы игры. Прекрасные примеры и глубокий анализ читатель найдет в работе Шеллинг [1971], гл.
II.
Выводы предыдущего примера легко обобщить на произвольную игру двух лиц G (XV Х2, и? и2).
Используя обозначения определения 5 гл. II, назовем і-выигрышем по Штакельбергу выигрыш игрока і в любом t-равновесии по Штакельбергу, обозначим его через St:
S; = sup ut(xv х2), где {/, /} = {1, 2}.
(Xux2)tBRj
Таким образом, S(. это выигрыш игрока і, действующего оптимально в качестве лидера. Будем говорить, что в игре G имеет место борьба за лидерство, если не существует такого исхода х, для которого:
Stu,(x), і=1, 2. (3)
Лемма 2. Предположим, что игра G имеет по крайней мере два оптимальных по Парето NE-ucxoda х1, х2 с различными векторами выигрышет
(иДх1), щ (л:1)) ф (,, (л;2), и2(х2)). (4)
Тогда в игре G имеет место борьба за лидерство.
Доказательство. Заметим, что NE (G) = BRl П BR2. Следовательно, по определению St имеем
{х g NE (G)} =Ф {ut (л;) S(, t= 1, 2}.
Если в игре G нет борьбы за лидерство, то найдется исход х, для которого справедливо (3), что означает
Щ (х'Х и, W, і=1, 2, иі (х ) иі (х), = 1, 2-
Поскольку х1 и л;2 оптимальны по Парето, то все четыре неравенства должны обратиться в равенства, что противоречит предположению (4).
В порядке дальнейшего обсуждения NЕ-исходов сравним их с исходами при сложном равновесии.
Теорема I. Предположим, что для всех і С N множества Х( конечны.
-
Если игра G = (Xit up, i ? N) разрешима по доминированию, то любое сложное равновесие является равновесием по Нэшу1).
Доказательство. Доказательство соответствует доказательству леммы 4 гл.
II. Сначала нужно убедиться в том, что для любого прямоугрльного подмножества Y = X Yt множества XN
(6 N
выполнено включение
NE (Z) с NE (Y), где Zf = , (up, Y),
a NE(Y)множество ?-исходов игры (Yh up, i?N).
Пусть X* = X Х\ обозначает множество сложных равнове-
І6 N
сий игры G, тогда
NE(X)z3NE(X1)=...=NE(Xt) = Xt. Щ
Итак, для разрешимых по доминированию игр сложное поведение всегда приводит к /Vf-исходу. Обратное утверждение отнюдь не верно.
NE-стратегия может быть доминируемой стратегией Этот факт является неожиданным. Проиллюстрируем его на примере игры 3x3 (т. е. игры двух лиц в нормальной форме, в которой каждый игрок имеет по три стратегии).
Здесь (Г, L)единственный NE-исход. Тем не менее, для игрока I (выбирающего строки), стратегия Т доминируется стратегией В, а для игрока 2 (выбирающего столбцы), стратегия L доминируется стратегией R. После исключения домини-
!) Из этой теоремы следует существование равновесий по Нэшу в играх в развернутой форме при условии взаимной однозначности (3) разд. 2 гл.
II. В отличие от случая разрешимости по доминированию это условие теперь может быть опущено. Для доказательства существования равновесий по Нэшу в игре в развернутой форме достаточно в алгоритме Куна каждой предфинальной вершине из L (М) приписать ход в финальную вершину с наибольшим выигрышем соответствующего игрока.
Прим, перев, руемых стратегий остается игра с нулевой суммой, в которой нет седловой пары.
Значение этого факта более наглядно для игр в развернутой форме.
Пример 3. Выборы с правом вето (продолжение)
,Із игры трех лиц примера 2 гл. II выделим игру двух лиц, предположив, что игрок 1 наложил вето на исходb (что соответствует его сложному поведению в силу заданных предпочтений). Тогда игроки 2 и 3 участвуют в следующей игре;
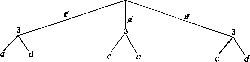
\u3(c)u3(a)u3(d)
Рис. 3
Имеется три ?-исхода: (/, R), (р1, L) и (ft, L).