ПОВЕДЕНИЕ ЛИДЕРА И ВЕДОМОГО
Пусть, например, существует yi?Yit для которого
Щ(Хі, х2)иі(уі, х2). (7)
Положим
Уі{Уі) = {у[ €УіЧуЛУг иіІУи У^щ{у[, у2)).
Мы утверждаем, что Yt (yt) имеет непустое пересечение с Zf. В частности, если гі доставляет максимум функции Ф( на УіІУі), где
Фі(уО= 2 ut(y[, yt),
У г
то можно проверить, что стратегия zf не доминируема в игре (Ух-, У3, и,). Следовательно, zt принадлежит множеству
УіЫПХі, и из (7) получаем
{хі, х2) (zj, х2),
что противоречит нашему предположению о том, что (%j, х2) седловая точка в (Zs, Z2, и^. Итак, доказано, что
S(ZX-, Z,)crS (У, У,).
Повторное применение данного включения приводит к следующей цепочке включений:
S(Xlt X,)^S(X\, X})=...=S(X1, Xi).
Далее, если игра G d-разрешима, то существует целое t, для которого все стратегии из Х\ эквивалентны для игрока і при условии, что стратегии игрока / ограничены множеством X) (определение 1). Для такого t мы, в частности, получаем
S(X(, ХІ) = Х{хХ{ = {сложные равновесия игры G}.
Это завершает доказательство леммы 4.
Следствие из теоремы 1 и леммы 4. Каждая конечная игра двух лиц с нулевой суммой в развернутой форме имеет цену. Каждый игрок имеет по крайней мере одну оптимальную стратегию.
Свойство (3) следует из и2 = иі. Иллюстрацией данного следствия является теорема Цермело\ в шахматах либо белые могут форсированно выиграть, либо черные могут форсированно выиграть, либо при правильной игре обеих сторон партия закончится вничью.
В действительности шахматы являются конечной игрой двух лиц с нулевой суммой в развернутой форме (с тремя значениями функции выигрыша: белые выигрывают, ничья, черные выигрывают), поскольку действует правило, по которому засчитывается ничья, при троекратном повторении на доске одной и той же позицииг).
Пример 3. Игра Ним
Для любого целого числа п^ 1 обозначим G* следующую игру двух лиц с нулевой суммой. Если л = 1, то G}тривиальная игра, в которой выигрывает игрок 1.
Если л 2, то игрок 1 должен выбрать целое число п{і 1. Далее, игрок 2 выбирает либо пи либо л2 = пЛі. Назовем nt выбором игрока 2. Тогда следующий шаг состоит в том, чтобы играть в игру G\. аналог игры Gn., где первый ход делает игрок 2. В частности, если либо пг, либо ла равно 1, игрок 2 выигрывает, выбирая данное число).
Это определяет игру в развернутой форме длины (л1). Из полученного выше следствия получаем, что множество N натуральных чисел разбивается на Н = N1\jN2y где А/,- есть множество тех п, при которых игрок і может гарантировано выиграть в игре G\. Проводя индуктивные по п рассуждения, получаем, что наше разбиение удовлетворяет следующим свойствам: 1 ? и, кроме того,
- I Vn?Nl(n'^s2) Злг, 1^/г^/г 1, и /г/гг€Мг,
\ Vn?N2 Vj 1) или пл1^Л^1.
Предоставляем читателю проверить, что эти условия дают следующий результат:
= \п\1, п Ър или п = Ьр 4 или п = Ьр 1}.
Рассмотрим теперь игры TJ, Г* с теми же правилами, за исключением того, что игрок, выбравший 1, проигрывает, другими словами, в игре Г{ игрок /, / Ф і, выигрывает.
Аналогичные соображения доказывают существование разбиения N = и М2, причем 1 € Л42 и (8) выполнено для Mt вместо Nt, і = 1, 2. Отсюда в свою очередь получается, что iVfjмножество четных чисел.
В качестве упражнения читатель может описать выигрывающие стратегии игрока 1 в G^, n?Niy и в игре Г?, пчетное и выигрывающие стратегии игрока 2 в Gh, п? и в Г?, п нечетное.
Задача 2. Мариенбадская игра
Фиксируем целое число р, р^ 1, и для любого набора п= (nlt ..., tip), где лг, ..., пр целые неотрицательные числа, определим игры Gj, G„ по индукции. Для данного п ^(0, ..., 0) скажем, что п' следует за п, если существует k, \^.k^.p, такое, что
i n'k, = nk, для всех k', 1 ^.k’ 1 р и k’ Ф k,
\ 0 n'ftnA.
Если п = (0.....0), то в игре G„ игрок і выигрывает. Если
п Ф (0, .., 0), то игра G„ разыгрывается следующим образом:
игрок і выбирает п', следующее за п. Если п' = (0, ..., 0), то игрок /, / Ф і, выигрывает партию, в противном случае начинается игра G„', в которой игрок / выбирает п, следующее за п', если п = (0, ..., 0), то игрок і выигрывает, иначе начинается игра Gf,„ и т. д.
Можно себе представить, что имеется р рядов спичек по nit ..., пр штук соответственно и каждый игрок последовательно забирает произвольное ненулевое количество спичек, но только из одного ряда. Игрок, который забирает последнюю спичку из последнего ряда, проигрывает. .
1) Докажите существование разбиения
[HU{0}Y = NiUNv
для которого, если n^N(, то игрок / может гарантированно выиграть в игре G„. Приведите условие, аналогичное (8), характеризующее это разбиение.
2) Для всех п = (п? ..., пр) обозначим через
n4 = a^af_, ... afcjf, 1
двоичное разложение nk, где I есть верхняя граница числа разрядов, необходимых для представления пи ..., пр, (следовательно, некоторые из чисел а\, ..., af могут быть нулевыми, но не все). Обозначим далее
р р
а0 = 2 о, - - - = 2 ar
й=і
Докажите, что N2 = M2U Р2, где
Л42 = {п?/, 0 //, fly четное и 3/, 1 / /, ау 0), /32={п?/, 1^/, fly = 0 и а0 нечетное число).
Задача 3, Топологическая дуэль (Шоке)
Пусть Еметрическое пространство. Обозначим через О множество непустых открытых подмножеств Е. Наша игра устроена так.
На шаге 1 игрок 1 выбирает Аг ? О.
На шаге 2 игрок 2 выбирает Л2^0 с единственным ограничением АісА1... .
На шаге t игрок (1, если t нечетно, и 2, если четно) выбирает At?0 с единственным ограничением Atc:At_1..., и так до бесконечности.
Скажем, что игрок 1 выигрывает, если
П АіФ'0.
t= I
Если это пересечение пусто, то скажем, что выигрывает игрок 2.
1) Докажите, что если Е полное метрическое пространство, то игрок 1 может гарантировать победу.
2) Докажите, что если E = Q, то игрок 2 может гарантировать победу.
3) Для любого ли Е наша игра имеет цену?
4. ПОВЕДЕНИЕ ЛИДЕРА И ВЕДОМОГО
Мы рассмотрели ситуации, в которых все игроки находятся на одном и том же уровне информированности (полное незнание гл, I и полная информация в этой главе). В ряде экономических приложений, в частности при олигополистической, конкуренции с доминирующей фирмой, естественным образом возникает несимметричное распределение информации.
С помощью теоремы Куна мы исследуем простейшую модель такого сорта: поведение типа лидерведомый в игре двух лиц 1).
Для данной игры двух лиц (Х^ Х2, и1г иг) обозначим через BRt график отображения наилучших ответов і-го игрока:
(хь х2) ? BRX ФФ их (xlt xt) = sup их (уи х2)
У\ € Хі
(симметричное определение для BR2).
Определение 5. Назовем {хх, х2) і-равновесием по Штакель-бергу в игре (Х1( Х2, их, и2), если
(AT!, x2)?BR. и U;(xx, xa)= sup і(г/х, y2), (9)
Wи Уг) 6 BRj
где і, / = 1, 2 и іф\.
Можно интерпретировать 1-равновесие по Штакельбергу на основе, следующего сценария: игрок 1 (лидер) знает обе функции выигрыша Uj и и2 и использует эту информацию для предсказания реакции игрока 2. Игрок 2 (ведомый) воспринимает стратегию игрока 1 как заданную экзогенно (обычно он не обращает внимания на функцию выигрыша игрока 1) и максимизирует собственный выигрыш, полагая, что стратегия игрока 1 хх фиксирована. Таким образом, игрок 1, имея первый ход и предвидя, что игрок 2 использует один из своих наилучших ответов на хи найдет оптимальное решение задачи (9).
Заметим, что если игрок 2 имеет несколько наилучших ответов на хи то в (9) предполагается, что он выберет наилуч-ший ответ по отношению к функции их. Это упрощающее предположение не оказывает существенного воздействия на дальнейшее изложение.
Поведение лидера ведомого было впервые рассмотрено экономистом Г. Штакельбергом (в начале этого столетия) при описании стратегий фирм, конкурирующих на одном и том же рынке (в условиях олигополии). В таких ситуациях нередко одна из фирм оказывается сильнее остальных и навязывает им свою цену. Концепция равновесия, описываемая определением 5,
Ч В отечественной литературе поведение этого типа первым исследовал ,Ю. Б. Гермейер (Гермейер [1971]).
Библиографию по играм гермейерского типа см. в (Гермейер [1976]). Соответствующий математический аппарат используется для анализа иерархических систем. Прим, перев, служит для анализа поведения такой фирмы. В гл.
VI мы опишем простую модель дуополии, в которой равновесия по Штакельбергу играют исключительно важную роль (см. пример 6 гл. VI). Принцип поведения, подразумеваемый определением б, весьма напоминает таковой при последовательном исключений доминируемых стратегий.
Следующий результат показывает, что равновесия по Штакельбергу сводятся к сложным равновесиям при надлежащем преобразовании исходной игры.
Лемма 5. Пусть G = (Xiy Х2, и? и2) конечная игра двух лиц, причем функции их и иг взаимно однозначны на Xj х Х2. Тогда существует единственное 1-равновесие по Штакельбергу, которое обозначим (xlt х2). Рассмотрим следующую игру G = (XU X*1, і, и2):
I X*' состоит из отображений т), действующих из Хх в Х2;
I Va:j € Xj, ?т]€Х2х' щ(хи ц) = и;(хи ті (лгг).
Тогда игра G разрешима по доминированию, причем единственное сложное равновесие есть (х? г), где т]стратегия наилучших ответов игрока 2, и Г[{х1) = хі.
Доказательство. Существование и единственность 1-равновесия по Штакельбергу следует из взаимной однозначности ut на XjxX2.
Игра G является нормальной формой игры в развернутой форме, в которой игрок 1 выбирает стратегию из Xf первым, а затем игрок 2, зная выбор игрока 1, выбирает свою стратегию из Х2. В игре G стратегия наилучших ответов т) является доминирующей стратегией игрока 2. В самом деле, для любого xt ? Xt и любой функции ц g Xf' имеем
йг (*і, гГ)=и2 (Хі, л(*і))= SUP *(- !. х*) (хі, ^ (xi))=ut (xt, л)-
Х% 6 А;
Наше предположение о взаимной однозначности полностью определяет тр Перед вторым раундом исключения доминируемых стратегий игрок 1 оказывается участником следующей игры (XJ, {т]}, иІУ н2), в которой его единственная доминирующая стратегия определяется так:
иі (,xf, т)) = Wj (я*, т] (х*)) ^ щ (xj, т] (xj)) = Mj (xj, Я) Для всех Xj.
В силу взаимной однозначности и2 график отображения т) совпадает с BR2. Следовательно, (х*, г) (х*)) есТь_1 -равновесие по Штакельбергу в нашей игре, и поэтому х?=Хі,
Заметим, что существование t-равновесия по Штакельбергу можно гарантировать при обычных топологических предположениях (Х1( Хг компакты, щ, иг непрерывны). Однако лемму 5 непосредственно обобщить не удается.
Пример 4. Процедура голосования по Ролсу Пусть А { 1,2, ...,7} есть множество из 7 кандидатов, среди которых 2 игрока должны выбрать единственного.
Каждый игрок в качестве своего предложения может расставить кандидатов в некотором порядке. Следовательно, стратегия есть взаимно однозначное отображение из А на А, причем если х,(а)=1, то аэто наилучший по мнению игрока кандидат (обман, конечно, разрешен). Обозначим через Z множество стратегий игроков 1 и 2. Для данной пары (х1; x^gZxZ выбирается кандидат n(xit х2), где
J я(хі, x2) = inf {aa€tf (*i, x2)},
S R(xit x2) = {a(E ЛI max [Х (a), x2 (a)] = min шах [х* (b), x2 (?)]}.
v fee A
Очевидно, что R (xf, x2) состоит не более чем из двух кандидатов. Данное правило подобрано так, чтобы выбирался кандидат, чья наихудшая оценка среди двух избирателей является наиболее высокой.
Поскольку игроки могут выбрать любую расстановку кандидатов, то возникает стратегическая игра. Обозначим через ии u2?Z истинные мнения игроков 1 и 2. Тогда избиратели являются участниками следующей игры в нормальной форме:
(Z, Z, ?tj о я, ы2 о я). (10)
(В качестве выигрыша игрока берется ранг избранного кандидата с отрицательным знаком. Напомним, что игроки стремятся к максимизации своих функций выигрыша.)
Вычислим теперь 1-равновесие по Штакельбергу в игре (10). Фиксируем стратегию x^^Z игрока 1. Заметим, что для всех х2 € Z выполнено
я (Xj, х2) = а =ф Xj (а) 4. (И)
Другими словами, предлагая Xf, игрок 1 отводит кандидатов х,_1(7), х,-1 (6), хг'(5). Это справедливо, поскольку по крайней мере один кандидат а в хр1 ({4, 3, 2, 1}) должен быть таким, что х2 (а) ^ 4, поэтому
щах (х} (а), х2 (а)) 4 шах (хг (?), х2 (?))
для всех Ь в хг1 (7, 6, 5}).
Отметим далее, что при данном .Kj игрок 2 может обеспечить избрание любого кандидата из ^({4, 3, 2, 1}):
Vag А [Xj(а)4] =[Зл:2 €Z я^, *,) = а]. (12)
Например, для того чтобы обеспечить избрание хГ1 (4), игрок 2 объявляет свое предпочтение так:
л (xh х2) = а, где и2 (а) = inf {и2 ф) xt ф) 4}. (13)
Отсюда, в частности, следует, что
?(хи х2) ? BR2 и2( п(хи а:2))4
(так как множество {л:1()^4} состоит из 4 элементов).
Следовательно, игрок 1 как лидер может обеспечить избрание кандидата из множества A2 = ujl({ 1, 2, 3, 4}). На самом деле, он может гарантировать выбор любого кандидата из А2 за счет подходящего сообщения. Например, для того чтобы обеспечить выбор а = и^1 (3), игрок 1 объявляет:
Это сообщение вызывает наилучший ответ х2, такой, что в силу (13) я(х*, х,) = а,
Наконец, заключаем, что выигрыш игрока 1 (выраженный в ранге избираемого кандидата) в любом 1-равновесии по Штакельбергу равен
Sx = inf \иг (а) I и2 (а) 4}.
- Если игроки поменяются ролями, то в силу симметрии получаем, что выигрыш (ранг избираемого кандидата) игрока 2 в любом 2-равновесии по Штакельбергу равен
- S2== inf {2 (а) I иі (аХ4Г
Интересное следствие состоит в том, что, вообще говоря, ранги Sj и S2 несовместны в следующем смысле:
не существует такого а, что и1(а)г^,!і и a2(a)^S2. (14)
Более точно, пара (f, и2) либо удовлетворяет (14), либо такова, что
I условия 1 (а*) ^ St и иг (а*) ^ S2 выполнены в точности для \ одного кандидата а*. Тогда = м( (а*) для t = 1, 2.
Если для пары функций (и*, и2) выполнено условие (14), то игра (10) представляет типичную борьбу за лидерство: если игроки информированы о предпочтениях друг друга, то оказывается выгодным иметь первый ход и вынудить другого игрока занять позицию ведомого. Мы детально исследуем этот вид конфликта в гл. VI разд. 4 в связи с анализом угроз.
См. также пример 2 и лемму 2, гл. III.
5. ДРУГИЕ ПРИЛОЖЕНИЯ ТЕОРЕМЫ КУНА
В заключение гл. II рассмотрим несколько примеров и задач, направленных на преодоление технических и концептуальных трудностей, связанных с понятием сложного поведения,
Когда множества стратегий Хг бесконечны при всех і ? N (хотя бы и компактны), то весьма трудно формально определить сложное поведение. Одна из причин состоит в том, что в процессе исключения доминируемых стратегий компактность множеств Х\ не гарантируется (см. задачу 2 гл. I). Далее, сходимость последовательности Xf, t ? N, к подмножеству эквивалентных стратегий может осуществиться только в пределе, отсюда дополнительные топологические трудности...
Наконец, предположение (3) о взаимной однозначности, которое является решающим при доказательстве теоремы Куна, теперь трудно обосновать. Эти трудности демонстрируются в следующем примере, а также в приведенных ниже задачах 4 и 5.
Пример 5. Дележ доллара при инфляции (Дутта, Дживерс [1981])
Участники {1, 2, ..., п\ делят доллар в соответствии со следующим правилом:
Шаг 1. Игрок 1 предлагает дележ л:1 = -{л:!.....л],}, где
П
2 *? = 1, х}^0 при всех i?N. Затем игроки 2, п имеют
= і
право выбора; утвердить х1 или отклонить его. Если все игроки соглашаются на х1, то этот дележ принимается. Если хотя бы один игрок отклоняет лг1, то переходим к шагу 2.
Шаг 2. Игрок 2 предлагает дележ хг на суд остальных игроков. Если они отказываются принять ха, то переходим к шагу 3.
Шаг 3. Игрок 3 делает предложение и т. д. Если дошли до шага п и предложение игрока п отклонено, то вся процедура начинается сначала с предложения игрока 1 и т. д.
Предположим, что доллар обесценивается за каждый период переговоров с коэффициентом дисконтирования т, 0 т 1. Так, во второй период от него остается 6=1 т, в период 3 только 62 подлежит дележу и т. д. Ясно, что если процедура переговоров о дележе будет продолжаться до бесконечности, то выигрыш каждого игрока становится нулем.
Предполагая существование сложного равновесия с исходом х* = {xf, ..., х*) (точное определение и теорему существова-ния см. в работе Рубинштейна [1980]), проведем обычные рассуждения, основанные на анализе стратегических ожиданий для вычисления х*. Предположим, игрок 1 на шаге 1 предлагает х1. Он знает, что игрок і, іфі, рассчитывает с шага 2, если таковой состоится, на равновесный исход (8х*, 8xf, 6xf, ..., 6xJ_i).
В самом деле, игра с шага 2 получается из исходной игры соответствующей перенумерацией игроков. Значит, для того чтобы предложение х1 было принято игроками 2, ..., п, необходимо, чтобы
х\^8х*, бх* - - - Xn^Sxt-i. (15)
Предполагая, что предложение х* будет принято, получаем xf ?8х*, ..., xt^6xt-i. (16)
Выберем теперь х\ так, чтобы
х\ 1 [6xf + 8xf + ... + 6л?_і],
тогда существует допустимый дележ (хі, х\, ..., х„), превращающий все неравенства из (15) в строгие и, следовательно, приемлемый для игроков 2, п. Значит, неравенство
X* 1[8xf 6a:?Li] противоречит оптимальности x+
(сложные равновесия являются равновесиями по Нэшутеорема Д гл. III). Таким образом, получаем
1 ¦- + ... + fix* j] = (1 - б) + Ьх* xf. (17)
Используя (16) и (17), получаем для всех і=1, ..., п xf V-'xt ^ (1 6) б‘"1 + 6‘х* ^ (1 6) 61'-1 + 6 xf,
откуда
* для всех *=1* - - - -
Выражения в правой части в сумме равны 1, поэтому все они суть равенства. Заметим, что когда 6 стремится к 1, предельный дележ становится справедливым (каждый игрок получает 1/п); тем не менее при 6=1 вся стратегическая аргументация оказывается некорректной.
Для того чтобы точно описать в следующем примере некооперативное поведение полностью информированных игроков, требуется уже комбинация концепций решения. А именно, усеченная после исключения доминируемых стратегий игра становится несущественной.
Пример 6. Дележ трога по Штейнгаузу
Пусть отрезок [0, 1] символизирует неоднородный пирог, который должен быть поделен между двумя игроками. Полезность доли А а. [О, 1] оценивается для игрока 1 величиной
?і(А)~ J (дx'jdx,
а полезность доли В с [0, 1] оценивается игроком 2 как
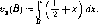
По мере того как время изменяется от t = 0 до t 1, нож двигается со скоростью 1отх = 0кх=1. В любой момент времени каждый из игроков может остановить нож.
Если нож остановлен в момент t игроком і, то этот игрок получает долю [0, /], а другой игрок\t, 1]. Значит, Xf=X2 = [0, 1], где стратегия х1 означает остановку в момент t = x-t игроком і, если другой игрок не остановил нож раньше. Функции выигрыша
определяются так:
щ(хи *2) =
Стратегия th і 1, 2, определяемая из условия
М[0. */]) = МІл-. П).
есть единственная осторожная стратегия игрока і. В самом деле, р(. (*,.)= inf и{(хи х2) inf [?{ ([0, х,]), ,([*„ 1])},
поэтому ф(- достигает максимума, когда доли [0, ^-] и [th 1] равноценны для игрока і.
При нашем специальном выборе о( имеем tt t2. Следовательно, при осторожном поведении игрок 1 получает долю [0, ^], а значит, свой гарантированный выигрыш аі = п,([0, ^]), в то время как игрок 2 оказывается более удачливым: v2§tu 1]) и2([/2, 1]) = а2. На самом деле, при осторожном поведении весь дополнительный по сравнению с гарантированными уровнями (cXj, а2) выигрыш оказывается распределен в пользу игрока 2, а именно:
?г(?и 1]) = max {,(**, хг)\щ(хь Jtr2)af}.
В гл. V мы скажем, что этот исход является наилучшей переговорной точкой для игрока 2.
Первый раунд исключения доминируемых стратегий дает
(н;) = [/,-, 1], поскольку стратегия х{ остановить нож до момента t{ доминируется осторожной стратегией (это легко проверить). Предположим теперь, что игрок 1 знает функцию выигрыша игрока 2 и поэтому может вычислить /2.
При условии, что игрок 2 не остановит нож до момента і2, второй раунд исключения доминируемых стратегий позволяет игроку 1 отбросить стратегии [/t-, t2). В самом деле, при всех х, 6 [^і, Q имеем
?і ([0, xtJ) = tif {х^, x2) C Щ (t2, x2) v ([0, /2]) при всех x2?\t2, 1].
Итак, XJ = [/2, 1] и дальнейшее исключение доминируемых стратегий невозможно, так как
Xl^Xi = [t2, 1] при 1^2.
Поскольку никакие две стратегии в Х‘( не эквивалентны для игрока і на то мы заключаем, что наша игра не раз
решима по доминированию. Тем не менее редуцированная игра ([*2. 1]. [^2.
1]. ии и2) является несущественной. В самом деле, у обоих игроков одинаковые осторожные стратегии = хг = t$
dj inf Mj (/2, x2) v-( ([0, /2]) inf Mj (a^j, л:2) = vj ([л^, 1])
I] I]
При Xf ti,
a2 = inf Ut(xu = 1J) inf u2(лГі, л:2) = v2([л:2, 1])
*,б[г„ i] с, еіб., ij
при л:2 f2.
Более того, (а4, а2) оптимальный по Парето вектор выигрышей (определение 5 гл. I), как это видно из рис. 5. Из теоремы 1 гл.
I заключаем, что хг = л:2 = ігоптимальные стратегии игроков в 2-редуцированной игре. Можно считать исход (t2, t2) соответствующим случаю полной информации игрока 1 о функции выигрыша 2. Заметим, что вектор (а„ а2) = {?г ([0, /2]), н2([*2, І])) оптимален по Парето и в исходной игре, причем перераспределяет весь дополнительный выигрыш в пользу игрока 1і
М[0. ^1) = max {и1 (лГі, х2)\и2(х^, x2)a2}.
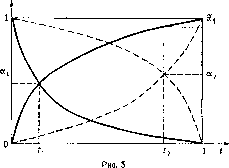
Две кривые, пересекающиеся в (tb aj), суть графики ^ (ГО, Л) и о*([(, 1])- Две пунктирные кривые - графики у2([0, t\) и v2{[t, 1]).
Упражнение 2. Каким будет некооперативное изолированное поведение, если нож двигается от х = 1 к х = 0?
Упражнение 3. Аукцион неделимого товара
Рассмотрим аукцион первого типа из примера 2 гл. I. Проведите последовательное исключение доминируемых стратегий (двух раундов будет достаточно).
Докажите, что эта игра не разрешима по доминированию и что редуцированная игра (после последовательного исключения) не является несущественной. Заметим, однако, что игрок 1 имеет единственную осторожную стратегию в этой игре, что позволяет говорить о естественном некооперативном исходе игры.
Задача 4. Метод деливыбирай
Теперь игрок 1 фиксирует [О, 1J, затем игрок 2 выбирает [0, хх] или [*!, 1] в качестве своей доли (игрок 1 получает оставшееся). Пусть предпочтения игроков описываются теми же полезностями, что и в примере 6.
1) Сформулируйте игру в нормальной форме.
2) Докажите, что каждый игрок имеет по одной осторожной стратегии и осторожное поведение позволяет игроку 2 присвоить весь дополнительный по сравнению с гарантированным выигрыш.
3) Предполагая, что игрок 2 при равенстве для него частей пирога делает благоприятный для игрока 1 выбор, докажите, что игра разрешима по доминированию и исход сложного равновесия отдает весь дополнительный выигрыш игроку 1.
Можете ли вы предложить модификацию определения 1, которая позволила бы ослабить последнее предположение и получить по существу то же поведение?
4) Какими будут t-равновесия по Штакельбергу в этой игре?
Дайте интерпретацию результатов.
Пример 7. Парадоксальный метод дележа
Пираты делят добычу: 100 слитков золота. Процедура дележа устроена следующим образом. Сначала самый старший пират предлагает дележ по своему выбору.
Если хотя бы половина пиратов согласна с этим дележом, то он считается принятым. В противном случае (т. е. если абсолютное большинство пиратов его отвергает) второй по старшинству пират предлагает новый дележ добычи среди оставшихся (п 1) пиратов.