ОСТОРОЖНЫЕ И ОПТИМАЛЬНЫЕ СТРАТЕГИИ
Если первому игроку известна ценность товара для остальных игроков, то он может исключить стратегии (а2, а,]. Мы разовьем эти соображения в гл. II (см., в частности, упр. 3).
В данной главе сосредоточим внимание на изолированном поведении, требующем знания только собственной функции выигрыша.
В аукционе второго типа (аукцион Викри) победителем считается также участник, предложивший наибольшую цену, однако он должен уплатить вторую по величине цену. Возникает следующая игра п лиц:
Хх= ... =Хп = [г, +оо).
Для всех х?Х{1 „} обозначим = sup х,.
1 / п
. І ^ 1
Тогда Uj(x) cijх_і, если і= inf /,
І € to (X)
и, (x) = О в противном случае.
Утверждается, что искренняя стратегия а{ является доминирующей стратегией і-го игрока. В самом деле, фиксируем исход x?Xn и выделим два случая.
Случай 1. Игрок і выигрывает на аукционе при исходе (ait х,).
Отсюда следует Заметим, что иі(х) = аіx_h еслиt-й игрок выигрывает аукцион также и при исходе*, и и((х)=О в противном случае. Следовательно,
;(*,-, х,)^аІх_і = иі(аі, х,).
Случай 2. Игрок і не выигрывает аукциона при исходе (а,-, *?).
Тогда а;^х_1, а значение функции , (*,-, хі) есть либо (,аі*_;), либо 0, поэтомуut(x,, */)0 = Ui(ait xt).
Легко можно убедиться в том, что нет другой доминирующей стратегии і-го игрока, значит, D(- (ие) {а(}, и равновесие в доминирующих стратегиях приводит к победе на аукционе первого игрока, который выплачивает цену а2. Этот исход доминируется по Парето исходом (г, ..., г). Если каждый игрок назначит начальную цену аукциона, то игрок 1 получит товар, заплатив всего лишь г.
Конечно, игроки {2, ..., п) не станут помогать игроку 1, если он не перераспределит часть своего сверхдохода а2-^-г между ними. Такое поведение было бы кооперативным, здесь оно не рассматривается. О нем см. в гл.
VI разд. 5.
Пример 3. Услуга за услугу
Если у одного участника есть несколько доминирующих стратегий, то они для него эквивалентны (см. лемму 2), но возможно не эквивалентны для остальных. Рассмотрим следующую игру двух лиц, в которой стратегии каждого участника влияют только на выигрыш другого, но не на свой собственный:
Игрок 2
Любой исход является равновесием в доминирующих стратегиях, но только один из них оптимален по Парето.
Задача I. Две олигополистические игры (Кейз [1979])
1) Игра с назначением цен в дуополии.
Два дуополиста предлагают на рынок взаимозаменяемую продукцию. Если они установили цены рг и р2, то соответствующий спрос на их продукцию будет равен:
единиц товара, произведенного игроком 1,
dt (у-)** единиц товара, произведенного игроком 2.
Предположим, что затраты на выпуск единицы продукции у обоих производителей не зависят от масштабов производства. Тогда приходим к следующей игре в нормальной форме:
иі(Рь Pt) = (Ptci)di, где С[ постоянная величина,
С{ 0, а, 1, t= 1, 2.
Вычислите равновесие в доминирующих стратегиях для этой игры и проанализируйте выбранную форму функций спроса.
2) Олигополия с назначением выпусков.
Предположим, что цена на некоторый товар с насыщаемым спросом (например, минеральную воду) убывает по экспоненте c-e~s, где Sсовокупное предложение.
Пусть количества минеральной воды, предлагаемой на рынке
п производителями, измеряются величинами хг.....хп, тогда
в предположении нулевых затрат получаем следующую игру;
ut(Xi.....хп) = сх;е-х'+-+Хп.
(Ответьте на те же вопросы, что и в 1.)
Задача 2. Топологические свойства множеств и D{
Пусть для всех i g N множество Х( компактно, а функция и, непрерывна на XN.
1) Докажите, что для любого игрока і единственная недоминируемая стратегия существует тогда и только тогда, когда у него имеется единственная доминирующая стратегия.
2) Покажите на примере, что множества @)t (и,) недоминируемых стратегий и множество исходов, оптимальных по Парето, не обязательно замкнуты. Что можно сказать о множествах D,- (и,) доминирующих стратегий?
Задача 3. Стратегически обоснованное правило голосования с упорядочением (Мулен [1980]))
Пусть (Л, есть (линейно) упорядоченное множество из р кандидатов, среди которых сообщество N {1, 2, ..., п) должно выбрать одного. Для любого нечетного К обозначим через тк следующее отображение из Ак в А: для всех (аь ..., ак) € Л*.
Таким образом, тк(аи ...,ак) является медианой (средним элементом) множества {аг, ..ак\ в соответствии с заданным порядком на Л.
Определим семейство правил голосования на Л. Пусть множество стратегий і-го игрока (множество предложений) есть просто X; = Л, а правило голосования имеет вид
¦. п-1)
Я (Xj, - . - , Хп)
где (xf, . ,.,х„) изменяется на Х{і.....„}, а а*, ...,an_t фик
сированные элементы множества А. В частности, полагая af= ... =ап_г inf а, получаем, что я^, ...,х„)= inf х,-.
аеА Кіл
Или, например, пусть щ=.. .=ay=inf a, aa/+i==...=an_j=sup а.
аеА аъА
Тогда (лгі, ...,*„) есть кандидат ранга / + 1. если только хи ..., расположены в порядке убывания относительно заданного порядка на А. Если для каждого участника і определить полезности и, на А, то правило голосования порождает следующую игру п лиц):
? = (-Xj, - - - і Кп, MjOJt, - .., ипоя).
1) Пусть х{ и Уі два соседних элемента А относительно заданного на этом множестве порядка. Докажите следующие предложения:
{иi (Х;) и, (у;} \x{ доминирует yt для игрока i\,
{и, (х,) = Ui(yt)\ {x, и yj эквивалентны для игрока і].
Выведите отсюда, что ®,(и,) состоит только из локальных максимумов ut, т. е.
Х{ € t (и,) =.[?^ € А {и, (х,) и, (г/,)} =
= Зг, € *г Уд {I (2,) И/ (*/)Н
уни-
2) Докажите, что если функция выигрыша и, игрока модальна на (А, *^), т. е.
За, Р ? А:
на (-, а] и, не убывает, на [а, Р] щ постоянна, на [Р, *¦) и, не возрастает,
то у игрока і есть доминирующая стратегия.
Каково множество D, (и,) в данном случае? Докажите, что равновесие в доминирующих стратегиях в игре g оптимально по Парето.
3) Для произвольных функций выигрыша и, на А докажите, что множество недоминируемых стратегий в играх g, полученных на основе правил голосования я,, . ..,яв_.„ имеет следующий вид;
для я„ . ..,яп_,- 3i(ui) = LM(ut) = {xi?A \х{ локальный максимум щ),
для я,- @i(ui) = {xi€LM(ul)\Vyl€LM(ul) [г/, х,] или ГІ(Уд
Задача 4. Механизм финансирования общественных благ по КларкуГроувзу (Грин, Лафон [1979])
Пусть А множество из р исходов (представляющих различные общественные проекты, кандидатов и т. п.), среди которых сообщество N должно выбрать один. В противоположность предыдущей задаче предположим, что допустимы побочные платежи (денежный обмен) и что участники имеют квазилинейные полезности. Так, если и,- действительная функция на А, представляющая полезность для і-го участника, то совокупная полезность определяется как M;(cz) + ^f, где а ?А является принятым решением, а число t{ (положительное) побочный платеж участнику і.
В механизме Кларка Гроувза каждый участник объявляет свою функцию полезности. Поскольку информация о функции и/ имеется только у і-го участника, он может выбрать любой вектор и утверждать, что это и есть его функция по
лезности. Следовательно, Х; = есть множество стратегий і-го игрока.
После того, как каждый игрок і объявляетх;, складывается исход x$XN. Решение cz* = cz* (х) ? Л выбирается из условия
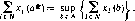
Побочный платеж игроку і есть tt (х):
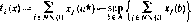
Следовательно, если (и;);6 nсовокупность истинных функций полезности, то получается следующая игра в нормальной форме:
g = (Xf, uh i?N), где ui(x) = ui(a*(x)) + ti(x).
Отметим, что отображение х а* (х) любое, удовлетворяющее (1).
1) Заметьте, что число tt(x) неположительно, и дайте интерпретацию случаям і,(х) = 0 и іг(х) 0.
2) Докажите, что искренняя стратегия xf = , является единственной (с точностью до аддитивной константы) доминирующей стратегией игрока і.
3) Докажите, что равновесие в доминирующих стратегиях и = (М()іе n оптимально по Парето тогда и только тогда, когда ti (а* (и)) 0 для всех і.
Дайте интерпретацию этому результату.
2. ОСТОРОЖНЫЕ И ОПТИМАЛЬНЫЕ СТРАТЕГИИ
Если у і-го игрока не имеется информации о функциях выигрыша остальных игроков, то он не может исключать из рассмотрения какие-либо допустимые стратегии из Xt (мы предполагаем, что множества стратегий всех игроков известны всем).
Один из способов исключения стратегий на множестве Х{ состоит в удалении доминируемых стратегий. Другой путь соответствует пессимистическому предположению (исключающему риск), что случится худшее.
Определение 4. В игре в нормальной форме (Х{, up i € A/) xi является осторожной стратегией /-го игрока, если выполнено
inf {Xj, Xt) = sup inf ut (у;, x ) = af.
x,sxt *,e X.
Обозначим через Pi(ut) множество осторожных стратегий t-ro игрока. Осторожное поведение реализуемо и совместимо с правилом исключения доминируемых стратегий.
Лемма 3. Предположим, что Х{компакты, а и( непрерывны для всех і ? N. Тогда множество Р{ (,.) осторожных стратегий і-го игрока не пусто, компактно и пересекается с множеством ); (и{) недоминируемых стратегий-
Р1(иі)(\@)і(иі)Ф0.
Доказательство. Фиксируем Поскольку функция и{
непрерывна, то функция ? (yt) inf иДуь хі) полунепрерывнаVsсверху) на Xt и, следовательно, множество ее точек максимума есть непустое компактное множество Р{(и{). Рассмотрим далее игру Н (Ул up у € N), где У; = X, для / Ф і и У, = Р{(и{).
По лемме 1 игрок і имеет по крайней мере одну недоминируемую стратегию хг в игре Н. Предположим, что х{ доминируется стратегией у{ в исходной игре (Xt, up, ig N), т. e.
[Vxf € X u{ (x{, xt) щ (y{, x/)] = f9 (x,) ? (yt)].
Отсюда ?(г/г)= sup ?(гг) и y{ € P{ (ut), что противоречит предположению о недоминируемости х( в игре Н. Значит, xt принадлежит Рг (и,) Л®,-(,-)- В
Н^ке в задаче 5 мы предполагаем другой вариант определения 4, который автоматически выделяет подмножество из множества Р{ (и,-) п @і (щ).
Используя осторожную стратегию, игрок і гарантирует себе выигрыш а;. Назовем аг гарантированным выигрышем.
Если набор (а,- ),¦= л/ гарантированных выигрышей является оптимальным пс) Парето, тогда мы считаем, что осторожные стратегии также могут быть названы оптимальными.
Определение 5. Скажем, что игра в нормальной форме несущественна, если нет исхода г/gX д, для которого
( ?і С N sup inf ,- (л:,-, хі) = сх,- sc; м,- (у)
^ xizxi xteX
[3i?N cti ut (у).
Название несущественные для данного класса игр на интуитивном уровне можно пояснить следующим примером. Имеется единица однородного товара, которая должна быть поделена среди членов сообщества N. Предположим, что игрок і за счет хорошей игры может гарантировать, что его окончательная доля будет не меньше а,{ независимо от поведения остальных игроков.
Допустим, что ? ,= 1. Тогда (a,)i€W есть дележтовара, который должен быть результатом оптимального поведения игроков).. В нашем более общем случае функции выигрыша игроков не являются сравнимыми, а потому их нельзя складывать.
Тем не менее, в несущественной игре осторожные стратегии оптимальны в следующем смысле.
Теорема I. Предположим, что (Х(, up, i ? N)несущественная игра. Пусть осторожная стратегия игрока і для всех і 6 N, и пусть хсоответствующий исход. Тогда
1) и( (х) = а,- ut (х;, у,) для всех i?N и yt? X,-,
2) хоптимальный по Парето исход,
3) для любой коалиции ScN и любого набора стратегий ys 6 Xs одновременное выполнение следующих двух условий невозможно:
iVtgS Ui(x)^Ui(ys, XSc),
\ Зі 6 S щ (х) и(ys, XSc).
Доказательство. Поскольку xtосторожная стратегия і-го игрока, то имеем
а; = inf ut (xt, yt) ^ и, (x). угех.
Данное неравенство выполнено для всех і, а поскольку наша игра несущественна, то а,- = ut (х) для всех і и утверждение 1 теоремы доказано.
Утверждение 2 следует из 3 при S = N. Для доказательства 3 выберем S и ys?Xs, такие, что
VigS а, ut (ys, xSc). (2)
Применяя утверждение 1 к / ? Sc, получаем Vj€Sc а^иДу^ xSc).
Объединяя две системы неравенств, получаем и{ (ys, xsc) = a{ для всех і, поскольку игра несущественна. Следовательно, строгое неравенство в (2) невозможно.
Согласно утверждению 1, если игрок і использует оптимальную (т. е. осторожную) стратегию и ожидает, что остальные игроки сделают то же самое, то он получит выигрыш, равный гарантированному аг. Если некоторые игроки /', Дфі откажутся от использования оптимальных стратегий, то это может быть только выгодно игроку і. Свойство 3 означает, что никакой отдельный игрок и никакая коалиция игроков не имеют причин для одностороннего отхода от осторожных стратегий (мы неявно предполагаем, что побочные платежи внутри коалиции невозможны, т. е. полезности не трансферабельны).
В терминах определения 1 гл. V набор осторожных стратегий является сильным равновесием.
Для того чтобы дать интерпретацию определению 5, рассмотрим также игру (Х;, up і ? N), которая не является несущественной, и заметим, что никакой набор стратегий х не может быть назван оптимальным.
В самом деле, два очевидных требования оптимальности суть а, ^ ti; (х) для всех і и оптимальность по Парето исхода х. По определению 5 эти условия вместе приводят к тому, что для некоторого і ? (V получается
sup inf и, (ус, уі) = а{ и, (х).
?і
Иначе говоря, игрок і не может себе гарантировать выигрыш и,- (х) и может подвергнуться угрозам со стороны дополнительной коалиции N\{i).
Основные примеры несущественных игр следует искать, конечно, среди игр двух лиц с нулевой суммой. Но об этом в следующем разделе.
Упражнение 1. Предположим, что g игра двух лиц, в которой равновесие в доминирующих стратегиях оптимально по Парето. Обязательно ли игра g несущественна?
Задача 5. Лексикографически осторожные стратегии (Му-лен [1981]).
Для каждого элемента г (zlf ..., zt) из IR7 результат переупорядочения его координат по возрастанию обозначим через г*:
г* = (ylt ..., уТ) {ух.....ут[ = {!.....Zt\,
УіУ*---Ут-
Введем далее лексикографический порядок в IRr:
Vt t0 yt = zb У и *t,.
Пусть (X,-, up i?N) игра в нормальной форме, причем множества Х(- конечны. Будем говорить, что стратегия х{ игрока і является лексикографически осторожной, если она максимизирует на множестве X,- по отношению к лексикографическому порядку в IRX? следующее отображение:
х{ = (и, (X;, x,)(xt€Xr)*.
Обозначим через LP(u{) множество лексикографически осторожных стратегий г'-го игрока.
1) Дайте интерпретацию введенного определения.
2) Докажите включение (u;) s Р; (и,) П (г).
3) Докажите, что понятие лексикографически осторожной стратегии обобщает понятие доминирующей стратегии в следующем смысле:
{Рі (,) Ф 0} = {LPi (,.) = D, (ц - ) = (и,)}.
3. ИГРЫ ДВУХ ЛИЦ С НУЛЕВОЙ СУММОЙ
Игры двух лиц с нулевой суммой имеют вид (Хх, Х2; щ, щ), т. е. игроки являются чистыми антагонистами. Обозначим такую игру через G = (Хх, Х2, uj, понимая под (положительный или отрицательный) платеж, который игрок 1 максимизирует, а игрок 2 минимизирует Тогда осторожные стратегии могут быть заданы так:
*і € Л (Щ) inf і(*і, yt) = sup inf ul(ylt y2),
У2€ X2 Уі € X! X2
€ p2 (1Ml) sup Щ (yu x2) = inf sup , (^, y2).
У\ € X, € Л2 г/, € X,
Числа sup inf u, и inf sup u, являются соответственно макси-
Vi Уг Уг Уі
мальным гарантированным выигрышем игрока 1 и минимальным гарантированным проигрышем игрока 2. Они связаны неравенством
sup inf щ sgi inf sup щ. (3)
Vi Уг Уг Vi
Для доказательства (3) фиксируем произвольные XjgXj, хг$Х2 и заметим, что
Фі (*і) = inf Щ (хи уг) щ (хи х2) sup Ui (уь х2) = ср2 (*t).
*/2 У
Отсюда следует
sup Фі (Уі) inf ф2 (y2).
Ух V?
Если выполнено равенство
sup inf щ = nf sup ut = a,
Уі */fi #2 Уі
то будем называть число а ценой игры G1). Если в (3) строгое неравенство, то будем говорить, что игра не имеет цены.
Теорема 2. Пусть G = (X(, Х2, щ) игра двух лиц с нулевой суммой.
Если игра имеет цену, то она несущественна. Обратно, предположим, что Х? Х2 компакты, а , непрерывна, тогда если G несущественна, то она имеет цену.
Ч Наряду с этим термином в отечественной литературе широко используется также термин значение игры. Прим, перев.
Доказательство. Предположим, что G имеет цену, и пусть исход (xt, xJgXj-xXj, таков, что
sup inf щ ^ их (хи х2),
У1 Уг М\
sup inf М, ^ MJ (хи х2) щ (хи х2) ^ inf sup Mj. v '
Уг Уі Уг Уі
Поскольку (3) обращается в равенство, то эти два нера' венства на самом деле тоже равенства, и первое утверждение доказано.
Предположим теперь, что (3) строгое неравенство. В силу сделанных топологических предположений и леммы 3 мы можем выбрать пару (л^, х2) € Рх (их) х Р2 (м2).
Эта пара удовлетворяет системе (4), в которой хотя бы одно из неравенств строгое, и поэтому игра G не может быть несущественной. Ц
Для несущественных игр с нулевой суммой пара оптимальных стратегий является седловой парой.
Определение 6. Седловая пара в игре двух лиц с нулевой суммой (Xt, Х2, Uj) есть такая пара (хи х2)$Х1хХг, что
?(Уіг i^^XfXXj ЧіІУи Хг)^:^і(ХІі Хг) ^:^і(ХІ Уг)-
Обозначим через S множество (возможно пустое) седловых пар.
Теорема 3. Пусть G = (Х{, Х2, их) игра двух лиц с нулевой суммой. Если G имеет цену, то исход является парой оптимальных стратегий тогда и только тогда, когда он является седловой парой: S Px (их) х Р2 (м2).
Если G не имеет цены, то в этой игре нет также и седловой пары.
Доказательство. Предположим сначала, что игра имеет цену и, следовательно, несущественна. По свойству 3 теоремы 1 получаем включение Рх (их) хР2(иг) ? S.
Обратно, выберем седловую пару. Из определения 6 получим
inf sup их sup их (ух, хг) их (хх, х2) inf Mi (xit у2) sup inf иь
Уг У1 Уі Уг Уі Уг
В силу (3) эти четыре неравенства огфащаются в равенство, а значит, хг осторожная стратегия игрока і (і = 1, 2). Ц
Теоремы 2 и 3 показывают, что ключевой характеристикой для игр с нулевой суммой является существование или отсутствие цены игры. Если игра обладает ценой, то оптимальные стратегии существуют и определяются эквивалентно двумя способами: изолированно (как осторожные стратегии) и одновременно обоими игроками (как седловые пары).
Пример 4
Пусть у обоих игроков имеется по 3 стратегии. Функция щ из хХ2 в R задана 3x3 матрицей, в которой строки соответствуют элементам множества Хи а столбцы элементам множества Х2.
Рассмотрим следующую функцию выигрыша.
У игрока 1 одна оптимальная стратегия (+), а у игрока 2 их две. Цена игры равна 1.
С другой стороны, игры без цены обычно порождают несходящуюся последовательность стратегических ожиданий. В самом деле, пусть (Хг, Х2, щ) игра с нулевой суммой, причем
sup inf і = а b = inf sup Uj.
Хх X2 X2 Xj
Скажем, что игрок 1 выигрывает, поднимая финальный платеж выше Ь, а игрок 2 удерживая финальный платеж ниже а. Допустим, что игрок 1 собирается использовать стратегию ас?. Предвидя этот выбор и используя наилучший ответ (стратегию х\), игрок 2 выигрывает:-
(ас?, х\) = inf щ (ас?, у2) а.
Ожидая, что второй игрок выберет хі, и используя наилучший ответ (стратегию ас?), игрок 1 выигрывает:
b sup і (уи хі) = щ (ас?, хі).
У\
И так далее... Для последовательности (асх, Ас?)/ел/, в которой х{ наилучший ответ второго игрока на ас?-’, а ас? наилучший ответ игрока 1 на х{, получаем
! (АС?-1, AC?)af и, (АС?, хі).
Следовательно, ни одна из двух последовательностей (АС?)ел/ и (ас?)6 л/ не сходится?) (в предположении непрерывности щ и компактности X, и Х2).
пример 5
Предположим, что игрок 1 собирается применить свою единственную осторожную стратегию х? Поскольку игроки принимают решения изолированно, то игрок 1, считая, что противник также планирует выбор единственной осторожной стратегии yit может отказаться от осторожной стратегии и применить наилучший ответ хг против стратегии уг и т. д.
Проиллюстрируем сказанное на следующем примере, в котором у каждого игрока имеется по одной оптимальной стратегии.
- хг-х^... -х2п х1=х3=...=х2п+1і
_,У2 = "Уад
-1 Уз=* - - =У2л+і
В заключение приведем пример игр с нулевой суммой без цены и с ценой, а также несколько упражнений и задач.
Пример 6. Раз два три
Каждый игрок выбирает одну из трех стратегий раз, два или три. Выигрыш первого игрока положителен, если он правильно угадал выбор второго игрока, и нуль в противном случае. Выигрыши задаются 3x3 матрицей:
грок 1 ¦
Гарантированный выигрыш игрока 1 равен 0, и любая его стратегия является осторожной, так как гарантирует только 0.
Гарантированный проигрыш игрока 2 равен 1, и у него единственная осторожная стратегия, а именно раз (поскольку два и три могут дать проигрыш величины 2 или 3).
В гл. IV мы будем использовать смешанные (рандомизиро-ваіные) стратегии для расширения рассмотренной выше игры до такой игры, которая имеет цену.
2 тез
Пример 7. Дуэль1)
Каждый из двух игроков может произвести один выстрел. Игроки сходятся с постоянной скоростью.
В момент t = О игроки достаточно далеко друг от друга, а в момент t= 1 сходятся вплотную. Задана действительная функция а( на отрезке [О, 1], измеряющая меткость игрока i, і=1, 2. Значение а,(/) есть вероятность того, что игрок і поразит игрока /, если будет стрелять в момент t. Предположим, что а,- не убывает, непрерывна и удовлетворяет краевым условиям а, (0) = 0 и а,( 1)= 1.
Выигрыш (игрока 1) равен -j-І, если первый игрок поражает второго до того, как сам будет поражен; 1 в симметричном случае и 0, если ни один не поражен, либо оба поражены одновременно.
Множества стратегий суть Х, = Х2 = [0, 1]. Стратегия х; игрока і означает
Я буду стрелять в момент t xb если противник не выстрелит раньше. Если же он выстрелит, но промахнется, то я для надежности буду стрелять в момент t= 1. Следовательно, нормальная форма игры имеет вид (Х„ Х2, и,), где
(5)
Uх (Х,, х2)
2aj (х,) 1, если х, х2, аі (хі) ~ a2 (*і). если х, = х2, 1 2a2 (х2), если х2 х,.
Например, пусть х, = ха. Тогда выигрышу +1 соответствует вероятность a, (х,) (1 a2 (х,)), т. е. игрок 1 попал, а его противник промахнулся.
Выигрышу 1 соответствует вероятность а2 (х2) (1 flj (х,)).
Вычислим осторожные стратегии игрока 1. В силу (5) легко проверить, что для любого х, € [0, 1]
Фі (х,) = inf и, (х„ х2) = inf {2 a, (х,) 1, 1 2a2 (х,)}.
*26[0, 1J
Пусть / есть отрезок, принадлежащий [0, 1] (возможно, и точка), определяемый из условия
/ = {Xj € [0, 1] I 2а, (х,) 1 = 1 2а, (х,)}.
Функция ср, возрастает до /, постоянна на / и убывает после /. Поэтому / = Р,(и,) является множеством осторожных стратегий игрока 1. Гарантированный выигрыш игрока 1 a, = sup inf и, есть общее значение функций 2а,1 и 1 2а„
X, X1
') Этот вид поединка иногда называют шумной дуэлью, чтобы отличить от бесшумной дуэли, когда игрок не слышит выстрела противника (см. упр. 3).
Прим, перев.
на /. Аналогично можно показать, что І Р2(иг) и гарантированный проигрыш второго игрока равен а*. Следовательно, аг есть цена игры, а / множество оптимальных стратегий для обоих игроков.