Мулен Э. - Теория игр
Книга французского математика, отражающая взаимосвязь между математической экономикой и теорией игр;,в последние годы на стыке этих двух наук получены интересные результаты. Изложение отличается методическими достоинствамиавтор дает возможность читателю самостоятельно разобраться в тщательно подобранных упражнениях.
ПРЕДИСЛОВИЕ
Теория игр принадлежит к числу важнейших математических инструментов современных социально-экономических наук. Автор данной книги ставил перед собой две основные цели.
1) Предложить неспециалистам замкнутое изложение основных понятий теории стратегических игр. Определения и результаты с математической точки зрения являются совершенно строгими. Вместе с тем обсуждению и сравнению различных понятий равновесия уделено большее место, чем развитию методов их вычисления. Технические детали в большинстве случаев опускаются.
Чтобы стимулировать читателей, предлагается более 75 упражнений и задач, некоторые из них достаточно трудны.
2) Обосновать полезность теоретико-игровых концепций для теоретического анализа социально-экономических ситуаций. Для этой цели были тщательно отобраны 39 ярких примеров.
В основном они почерпнуты из микроэкономических проблем: приведены примеры, относящиеся к теории несовершенной конкуренции, теории общественных благ, рассмотрены модели голосования, методы дележа и т. д. Во многих задачах читателю предлагается развить интерпретацию игровой модели. Для этого было бы полезно некоторое знакомство с логикой экономических рассуждений.
Некоторые важные разделы современных теоретико-игровых исследований в данной книге не рассмотрены. Наибольший пробел исследование игр с неполной информацией, поскольку, по моему мнению, результатам в этой области недостает завершенности и простоты, необходимой для учебника.
Опущено также изложение аксиоматического подхода к решению игр в форме характеристической функции, поскольку я отнес бы их скорее к нестратегическому анализу общественного выбора (см. введение).
Исходным материалом для этой книги послужили лекции курса теории игр, прочитанного в Национальном институте статиста-
ки и экономического управления. Я особенно благодарен Полю Шамсору, который был инициатором этого курса.
Я глубоко признателен Центру математической теории принятия решений Парижского университета, где я начинал изучать теорию игр под руководством Жана-Пьера Обена и Ивара Экланда, а также лаборатории эконометрики Политехнической Школы, поддержка которой обеспечила выход этой монографии в свет, благодаря Вильме де Суза, Мартине Видони и Мари-Элен Понруа, очень хорошо напечатавших рукопись.
Я также благодарен Эндрю Шоттеру, убедившему меня подготовить английский вариант книги, и Институту математических исследований в социальных науках в Стэнфорде, гостеприимство которого позволило мне завершить работу.
Эрве Мулен
ВВЕДЕНИЕ
Игра это идеализированная математическая модель коллек-тивного поведения: несколько индивидуумов (участников, игроков) влияют на ситуацию (исход игры), причем их интересы (их выигрыши при различных возможных ситуациях) различны. Антагонизм интересов рождает конфликт, в то время как совпадение интересов сводит игру к чистой координации, для осуществления которой единственным разумным поведением является кооперация. В большинстве игр, возникающих из анализа социально-экономических ситуаций, интересы не являются ни строго антагонистическими, ни точно совпадающими.
Продавец и покупатель согласны, что в их общих интересах договориться о 'продаже, конечно, при условии, что сделка выгодна обоим. Однако они энергично торгуются при выборе конкретной цены в пределах, определяющихся условиями взаимной выгодности сделки. Подобно этому рядовые избиратели, как правило, согласны отвести кандидатов,, представляющих крайние точки зрения. Однако при избрании одного из двух кандидатов, предлагающих различные компромиссные решения, возникает ожесточенная борьба.
Немного поразмыслив, читатель, наверное, согласится с тем, что большинство напоминающих игры ситуаций общественной жизни порождают как конфликтное, так и кооперативное поведение. По нашему мнению, теория игр является полезным логическим аппаратом для анализа мотивов поведения участников в подобных ситуациях. Она располагает целым арсеналом формализованных сценариев поведения, начиная с некооперативного поведения (гл. I) и до кооперативных соглашений с использованием взаимных угроз (гл.
VI). Для каждой игры в нормальной форме использование различных кооперативных и иекооперативиых концепций равновесия, как правило, приводит к различным исходам.
Их сравнение является основным принципом теоретико-игрового анализа и, по-видимому, источником строгих и вместе с тем содержательных рассуждений о побудительных мотивах поведения, вытекающих только из структуры игры в нормальной форме.
Во многих социальных науках имеется большое количество моделей, при анализе которых требуется изучать способы выбора стратегий. Приложения теории игр преимущественно развиваются в связи с исследованием экономики. Это соответствует установкам основоположников теории игр фон Неймана и Мор-генштериа. Однако прочная репутация теоретико-игрового подхода утвердилась только после теоремы Дебре Скарфа, позволяющей рассматривать конкурентное равновесие как результат кооперативных действий.
С тех пор целые разделы экономической теории (такие, как теория несовершенной конкуренции или теория экономического стимулирования) развиваются в тесном контакте с теорией игр (см. обзор Шоттера и Шведиауэра ?1980]).
Начиная с книги Фаркуарсона [1969], анализ процедур голосования, направленный на изучение стратегических возможностей, позволил переосмыслить некоторые традиционные направления политической теории. Хотя используемые при этом Игровые модели по-прежнему вызывают споры, достаточно ясно, jlTO потенциальные возможности теоретико-игрового подхода значительны.
Отсылаем читателя к обзорной работе Брамса [1975] и к последним работам по стратегической реализуемости (Мулен [1981]).
Теоретико-игровой способ мышления является сейчас достаточно общим в социологии (см. Крозье [1977]).
Ясно, что поиск равновесных концепций, являющихся идеализацией целого спектра некооперативных и кооперативных схем поведения, Тесно связан с основами социологии. В частности, наша точка Зрения на кооперацию как на необязательные соглашения (часть II), безусловно, восходит к идеям Руссо об эволюции от естественной свободы к гражданской свободе (см. Руссо [1755]). Тем не менее в современных социологических исследованиях формальные теоретико-игровые модели весьма редки и с математической точки зрения элементарны.
И все-таки влияние теории игр кажется нам уже необратимым, по крайней мере на этапе обучения.
Обзор содержания книги
В части I изучается некооперативное поведение изолированных игроков. Само задание игры в нормальной форме предполагает, что все переменные модели распределены между игроками, которые распоряжаются их выбором по собственному желанию (таким образом, все переменные модели становятся определенными после того, как каждый игрок зафиксирует свою стратегию).
Вначале мы предполагаем, что обмен информацией между игроками невозможен. При этом выдвигается несколько логически обоснованных способов выбора игроком стратегии, которой он должен придерживаться. К таким понятиям следует отнести доминирующие и осторожные стратегии, когда мы предполагаем, что игрок не знает предпочтений остальных игроков (гл. 1), а также сложное поведение, когда мы считаем, что все предпочтения игроков известны каждому участнику игры (гл.
II). Эти стратегии могут быть рассчитаны каждым игроком независимо от поведения других игроков.
Указанные понятия являются статическими. К сожалению, сколь бы привлекательны ни были эти понятия, их математические, свойства являются плохими (в частности, равновесие в доминирующих стратегиях и сложное равновесие, как правило, не существуют). Поэтому мы переходим к рассмотрению концепций некооперативного равновесия второго уровня, а именно, равновесия по Нэшу, которое требует некоторых контактов между игроками хотя бы на уровне совместного наблюдения за происходящим (гл.
III). Предлагается несколько сценариев поведения, обосновывающих определение равновесия по Нэшу; все они требуют перехода к динамике (хотя бы из двух периодов). В отличие от понятий первого уровня, исходы игры, равновесные по Нэшу, обладают хорошими математическими свойствами.
Если игроки используют независимые рандомизированные стратегии, то существование таких исходов можно гарантировать в весьма широких предположениях (гл. IV).
Основная причина перехода от понятий ч. I к понятиям ч. II (кооперативное поведение игроков) состоит в том, что индивидуальная свобода выбора стратегий наносит ущерб общественным интересам. Некооперативное равновесие (является ли оно следствием изолированного поведения, как в гл.
I и II, или удовлетворяет условиям стабильности по Нэшу, как в гл. Ill и IV) может не быть оптимумом Парето. Свободный выбор игроком своей стратегии противоречит требованию эффективности коллективного выбора в том (и только том) случае, когда для каждого оптимального по Парето исхода найдется выгодное с точки зрения какого-либо игрока отклонение.
В этом случае оптимальные по Парето исходы игры нельзя считать правдоподобными. Дилемма заключенного (пример 1 гл.
I) является хорошо известным примером такого противоречия. Это простейший пример противоречия между стабильностью и эффективностью, которое мы считаем главным побудительным мотивом к кооперации.
К сожалению, сами механизмы кооперации являются не столь наглядными.
Для того чтобы получить исходы, лучшие по Парето,, чем некооперативное равновесие, мы предполагаем, что игроки заключают необязательные соглашения. Это такие сценарии поведения, которые не лишают игроков их неотъемлемого права.
придерживаться любой стратегии, находящейся в их распоряжении. Эти соглашения автоматически выполняются благодаря свойству стабильности, которое аналогично свойству, введенному Нэшом: Меня никто не принуждает следовать нашему соглашению, но до тех пор, пока вы, все остальные, ему верны, у меня нет причин его нарушать. На самом деле, понятие равновесия по Нэшу это исторически первый существенный пример кооперативного соглашения такого типа.
Концепции гл. V последовательно развивают различные стороны определения Нэша. Мы сотрудничаем, потому что мы хотим этого, однако добровольная кооперация приводит к обязанностям для нас неожиданным (Дюркгейм [1893]).
Необязательные соглашения полностью признают право свободного выбора игроком своих стратегий. Однако реализуемость таких соглашений требует определенных ограничений на обмен информацией между игроками.
Одна из возможностейзапретить по достижении соглашения дальнейшие переговоры с тем, чтобы участники не могли больше угрожать друг другу. Этот путь приводит к понятиям стабильности гл.
V. Другая возможность состоит в том, чтобы любые отклонения от договоренности (в выборе стратегии) становились известными всем и потому можно было бы своевремен-во привести в исполнение взаимные угрозы. Это приводит к кооперативной точке зрения на предостережения, которым посвящена гл.
VI.
Мы не касаемся обязательных соглашений, поскольку тут Возникает целый круг вопросов, не связанных с выбором стратегий, а скорее относящихся к теории общественного выбора. Под обязательным соглашением мы понимаем договоренность игроков о некотором исходе игры, причем выполнение этой договоренности обеспечивается некоторым контролирующим органом. После подписания такого соглашения игроки фактически лишаются контроля над своими стратегиями. Следовательно, вопросы стабильности соглашений отпадают, поскольку никакие нарушения договоренности ни отдельным игроком, ни коалицией игроков больше не возможны.
Таким образом, все сложные проблемы кооперации снимаются после того, как соглашение подписано, зато все они возникают до подписания. Другими словами, поскольку теперь нет смысла сравнивать соглашения с точки зрения их стабильности, приходится говорить об их большей или меньшей справедливости.
Таким образом, подход к кооперации из описательного (какие соглашения являются стабильными при той или иной информационной структуре?) превращается в нормативный (какие соглашения считать справедливыми при заданных соотношениях сил отдельных игроков и коалиций?). При этом главная аксиома состоит в том, что справедливость это первичный побудительный мотив к кооперации, или, другими словами, несправедливость является решающей причиной разрушения кооперации.
Если хотя бы одному положению суждено остаться неизменным в будущем в теории стратегических игр, то это, по-видимому, будет утверждение о том, что данной игре адекватно несколько, не слишком много, равновесных концепций, в зависимости от условий обмена информацией и кооперации. И значит, игра в нормальной форме, наша основная математическая модель, действительно является богатым источником стратегических сценариев, проясняющих логические связи таких первичных понятий, как кооперативное и эгоистическое поведение, взаимные стратегические ожидания, тактическая неопределенность и ограничение информированности при кооперации, обмен угрозами и обещаниями.
Критика предложенных концепций должна основываться на их приемлемости в приведенных примерах.
Изучение равновесных концепций приводит к ряду теорем существования, а также к некоторым контрпримерам. Однако пустоту, скажем, a-ядра некоторой конкретной игры в нормальной форме не следует интерпретировать как логическое обоснование невозможности кооперации с помощью угроз в этой игре.
Скорее это означает, что сценарий предостережений, который лежит в основе определения a-ядра, не описывает полностью коалиционное поведение, и нужны другие, более сложные схемы (как правило, это двухшаговые концепции, см. гл. VI, разд.
2). Скромность создателя математических моделей требует избегать апокалиптических интерпретаций.
Некооперативное поведение игроков
Основной моделью для анализа некооперативного поведения является игра в нормальной форме.
Определение. Пусть N фиксированное конечное сообщество, скажем множество игроков (участников), для обозначения которых используется индекс і.
Игрой в нормальной форме называется совокупность, содержащая для каждого игрока і € N
множество стратегий Х{, элементы которого обозначаются я,-,
функцию выигрыша (функцию полезности) иь являющуюся Отображением из XN = X Х(- в R1’. Элемент х = (xf); е ді из мно-
І € N
жества XN называется исходом игры.
Игрок і выбирает любую стратегию xt € Xt. После того как каждый игрок выбрал свою стратегию, определяются исход х И выигрыш і-го игрока а,- (х).
Отметим, что в описанной выше модели нет ни случайных ходов, ни игрока, который бы моделировал неопределенность, свойственную природе.
*) В книге без пояснений используются общепринятые обозначения! В частности, IR множество вещественных чисел.
Прим, перев.
ГЛАВА I
НЕКООПЕРАТИВНОЕ ПОВЕДЕНИЕ ИЗОЛИРОВАННЫХ ИГРОКОВ
Рассмотрим игру в нормальной форме (Х{, ut\ i$N) и предположим, что игроки в этой игре действуют изолированно, т. е. каждый игрок выбирает свою стратегию независимо, не обращая внимания на то, какие стратегии выбирают другие участники. Игроки не обмениваются информацией. На выборы игроков не оказывает влияния прошлое (предыстория партии игры или начальная позиция).
Напротив, все стратегии априори считаются эквивалентными, и их различие должно устанавливаться, исходя из внутренних принципов оптимальности.
На протяжении гл. I будем считать, что каждому игроку известна его собственная функция выигрыша; функций выигрыша остальных игроков он может не знать.
В этих предположениях исследуем по очереди два не противоречащих друг другу сценария поведения изолированных игроков: сначала исключение доминируемых стратегий, а потом осторожное (максиминное) поведение.
1. ДОМИНИРУЮЩИЕ И НЕДОМИНИРУЕМЫЕ СТРАТЕГИИ
Определение 1. Стратегия х{ игрока і в игре в нормальной форме (Х{, ut\ і € X) доминирует стратегию у{, если
Ух, € X, ut(y{, Xi)s^Ui(x(y xt),
Эх, € X, u,(yit xt) щ {xt, xt),
где Xt= X X, и (x,, xt)€XN.
16N\V) '
Обозначим через S)i(ut) множество всех недоминируемых стратегий і-го игрока:
У1$@){(и{) % XjgXp xt доминирует у{.
Стратегия і-го игрока х( доминирует стратегию у{, если независимо от поведения остального мира N\{i} стратегия у{ для него не дает большего выигрыша, чем х(, а для некоторого
допустимого стратегического выбора игроков П\{і\ ему выгоднее выбрать х{, чем у{. Отсюда следует, что игроку і имеет смысл выбирать стратегию только из множества (ut).
Заметим, что t-му игроку для вычисления S){ (ut) достаточно знать множества стратегий Ху своих партнеров; знание их функций выигрыша не требуется.
Определение 2. Стратегия xt игрока і в игре в нормальной форме (Xі, и{\ і ? N) называется доминирующей стратегией), если
VxtZXf. и/(у;, xt),(*„ xt).
Обозначим через множество всех доминирующих стра
тегий і-го игрока.
Исход x = (Xj)t s jv назовем равновесием в доминирующих стратегиях, если х{ является доминирующей стратегией і-го игрока при всех і.
Недоминируемые стратегии существуют при достаточно слабых топологических предположениях, поэтому постулат о том, что при некооперативном поведении игрок исключает доминируемые стратегии, не приводит к логическому противоречию.
Лемма 1. Предположим, что для любого i^N множество X. компактно, а функция и1 непрерывна. Тогда множество (и,) недоминируемых стратегий і-го игрока не пусто.
Доказательство. Для любого / выберем вероятностное распределение ру на Xj таким образом, чтобы каждое непустое открытое подмножество Xj имело положительную меру). Зафиксируем і и рассмотрим функцию ф,-, определенную на Х(:
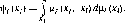
ІФі
Поскольку функция и{ непрерывна, то непрерывна и функция ф/( а следовательно, можно выбрать стратегию xf, максимизирующую функцию ф; на множестве X,-. Покажем, что стратегия xf недоминируема. В самом деле, если существует стратегия X;, доминирующая xf, то в силу непрерывности функции щ найдется открытое подмножество Ot множества Xt, такое, что
?ЛГ/ € Оі U; (xf, Xt) U, (X;, X,).
В силу выбора ру, іфі, получаем
^ и; {xf, xt) dp (х;) jj ut{xh xt) dp? (xt). ot o,
Поскольку неравенство и,- {xf, x!) ^ ut (x{, xt) справедливо на всем множестве Xt, то имеем1)
I U; {xf, xt) d pi (xt) J Uj (xh xi) dp? (xt).
Складывая два неравенства, приходим к противоречию:
^ (xf) ф,- (xt). ¦
В противоположность полученному выше результату доминирующие стратегии могут не существовать даже в топологически тривиальных (конечных) играх.
В самом деле, доминирующая стратегия х{ должна одновременно быть решением задач максимизации
шах іі/ (xh Xt)
х;ех.
при всех значениях параметра хг ? X,-.
Стратегии х,- и у{ і-го игрока будем считать эквивалентными, если они не различимы с его точки зрения:
?Хі € Xi U;{X;, Xt) = ui{y;, Xt).
Лемма 2. Предположим, что в игре в нормальной форме (Xj, up, j g N) множество недоминируемых стратегий і-го игрока непусто'. S). (ц;.) ф 0. Тогда эквивалентны следующие три утверждения:г)
(i) Существует доминирующая стратегия і-го игрокаі Dt (иі) ф 0.
(ii) Все стратегии в множестве S, (и,-) эквивалентны.
(iii) Dt (щ) = й, (и,).
Доказательство леммы 2 оставляется читателю в качестве (элементарного) упражнения.
*) Здесь и далее Асдополнение к множеству Л, Прим, перев.
2) Для того чтобы утверждения (і) (ііі) следовали из (іі), достаточна потребовать компактность множеств Ху и непрерывность функций Uj, j?N. Без этого предположения лемма, вообще говоря, не верна.
Прим, перев.
В лемме 2 говорится о том, что если у игрока есть хотя бы одна доминирующая стратегия, то все доминирующие стратегии эквивалентны и совпадают с его недоминируемыми стратегиями. В этом случае будем считать, что при некооперативном поведении игрок использует одну из них. С другой стороны, если у і'-го игрока нет доминирующей стратегии (наиболее частный случай), то его недоминируемые стратегии не эквивалентны, поэтому его некооперативное поведение не может быть определено однозначно.
Требуются дополнительные предположения об информации, которой располагают игроки (в частности, о функциях выигрыша), чтобы сделать дальнейшие заключения; см. разд, 2 ниже и гл. II.
Равновесие в доминирующих стратегиях постулируется рациональным некооперативным поведением изолированных игроков.
В приведенных ниже примерах 2 и 3 показано, что равновесие в доминирующих стратегиях может быть доминируемым по Парето (см. определение 3), что делает это понятие уязвимым при кооперативном поведении игроков.
Пример I. Дилемма заключенного (Льюс и Райфа [1957]) Каждый из двух игроков располагает двумя стратегиями А и Р, где А обозначает агрессивность, а Рмиролюбие. Предположим, что мир (оба игрока миролюбивы) лучше для обоих игроков, чем война (оба игрока агрессивны), но односторонняя агрессия (один игрок агрессивный, а другой миролюбивый) выгоднее агрессору. Типичная структура выигрышей имеет следующий вид:
| Игрок 1 |
|
||||
| ^2 А2 . Игрок 2 |
Для обоих игроков стратегия А доминирует стратегию Р. Таким образом, единственное равновесие в доминирующих стратегиях имеет вид (Аи Л2), т. е. постулируется, что результатом некооперативного поведения является война. В то же время исход (Pj, Р2) (мир) дает большой выигрыш сразу для обоих игроков. Таким образом, некооперативное эгоистическое рациональное поведение вступает в противоречие с коллективными интересами. Коллективные интересы диктуют выбор мирных стратегий. В то же время, если игроки не обмениваются информацией (так что, например, не могут возникнуть взаимные угрозы типа: Я буду миролюбив, до тех пор пока ты будешь миролюбив; подробнее об этом см. в гл. VI), война является наиболее вероятным исходом: изолированность стратегических выборов может нанести определенный ущерб общественным интересам.
Определение 3. Исход х € XN в игре в нормальной форме (X/, и.;\ i$N) доминирует по Парето исход y?XN, если
I Vi?N ,.(г/Х ,- (*),
\3i?N U; (if) U; (х).
Исход х назовем оптимальным по Парето (или оптимумом Парето), если он не доминируем по Парето.
В следующем примере равновесие в доминирующих стратегиях также доминируемо по Парето.
Пример 2. Аукцион неделимого товара
Товар должен быть куплен одним из п участников. Его ценность для і-го участника измеряется величиной ah причем предполагается, что с ростом і величины а,- не возрастают, т. е.
Будем рассматривать два типа аукционов. На аукционе первого типа каждый участник независимо предлагает цену. Пусть, например, і-й участник выбрал цену х;. Победителем считается тот, кто предложил наиболее высокую цену. Эта цена выплачивается продавцу товара. Обозначим через г начальную цену, назначаемую продавцом, т. е. ценность товара для продавца, и предположим, что г^ап. Складывается следующая игра п лиц:
Х,= ... = Хп = [г, +оо),
ДЛЯ ВСЯКОГО X(;X{1.....п) ПОЛОЖИМ W (х) = {i/Xj = sup дсЛ.
1 / л
Тогда и/(х) = а/хь если i= inf /,
/' € w IX)
и{(х) = 0 в противном случае.
Заметим, что при одинаковых ценах предпочтение отдается тому игроку, для которого ценность товара больше. Покажем, что а,-, т. е. искренняя стратегия і-го игрока, доминирует всякую стратегию X;, для которой выполнено а, хг В самом деле, Щ (Х(, 0 = и; (а,-, Хі) для любого xt. Значит, 3t (и,) = [г, а;].
Тем не менее у і-го игрока нет доминирующей стратегии, если только га,.
Для исключения доминируемых стратегий нужно знать только свою собственную функцию выигрыша.