КЛАССИФИКАЦИЯ ИГР ДВУХ ЛИЦ
Заметим, что стратегия of игрока і в повторяющейся игре является объектом весьма сложной структуры. Эта стратегия на каждом шаге t?N сопоставляет предыстории х1, ...,xt~1 выбор х{ игрока і. В действительности для реализации вектора выигрышей uN(x*) как вектора і?Б'-выигрышей в повторяющейся игре достаточно рассмотреть весьма простой исход о*. Стратегия of игрока і, которую он использует по соглашению, есть чистая стратегия xf до тех пор, пока никакой игрок / не отклонился от xf Если отклонившийся игрок / обнаружен, то стратегия af впредь диктует наказание данного игрока.
Поскольку мы интересуемся только равновесиями по Нэшу, то коалиционные отклонения от о* пока не учитываются.
Для того чтобы формально описать данный NE-исход, длякаждого j?N выберем стратегию х\ игроков N\{j], такую,7*ЧТОsup И) = Р/.хі
Для каждого і € N стратегия of игрока і в повторяющейся игре определяется следующим образом:хj = xf: в момент 1 выбирать
если х = х2 ... х~х = х*, то x\ = xf\ в момент t придерживаться условленной стратегии, если все остальные игроки до сих пор делали то же самое;
если х = х2 = ... х~2 Ф х*~г, тогда выбрать /, такое, что х]~гфх*, и далее играть х[ = х[ = х[+і = .. ¦ .
При каких условиях поведение, определяемое по о*, предостерегает игроков от отклонений в одиночку? Краткосрочный доход игрока і от отклонения в момент t (которому нельзя ничего противопоставить до следующей партии) должен перекрываться долгосрочными потерями от наказующего поведения игроков Н\{і} (которые по предположению придерживаются стратегии в моменты времени / + 1, / + 2, ...).
Полагаяи* ixf) = sup ut (х{, х?)xiи сравнивая дисконтированное значение в момент t краткосрочного дохода и* (xf)м,- (х*) с долгосрочными потерями, получаем следующее свойство стабильностиі
и* (xf) U{ (X*) б (щ (X*) 0() + Ь2{Щ (**) fy) Н- . . которое эквивалентно системе неравенств
1б.....и‘ ) для всех i$N, (14)
Таким образом, если б достаточно близко к 1, условия (14) выполнены, и, следовательно, о* является NE-исходом повторяющейся игры (с дисконтированным выигрышем (13) или со средним Чезаро (12)).
Лемма 4. Если система (14) справедлива, то повторенш игры G с дисконтированным выигрышем (13) имеет равновесный по Нэшу исход, которому соответствует последовательность исходов
х* =x = г
Таким образом, NE-выигрьш игрока і равен и{ (х*).
Заметим, что мы не описали полностью множество NE-исходов, возникающих при повторении игры G. Известно (см. Думай [1978]), что множество векторов выигрышей, соответствующих N P-исходам, может разрывным образом зависеть от б.
Приведем пример, который демонстрирует другой подход к повторяющимся играм. В этом примере каждый игрок принимает во внимание только последние наблюденные ходы своих партнеров.
Пример 4. Повторение игры дилемма заключенного (Думай [1978])
Предположим, что игра дилемма заключенного (пример 1, гл. 1) повторяется во времени и каждый игрок использует стационарную стратегию с памятью на один ход). Таким образом, стратегией игрока і является тройка (х(; yit г{), где xit yt, г{ принадлежат множеству {Л, Р} и интерпретируются следующим образом:
1) игрок і выбирает х^х] в первом повторении игры
2) в момент t 2 игрок I выбирает у{, если игрок / вел себя мирно в момент времени t 1, и ведет себя агрессивно, если игрок / был агрессивен, т. е.
х\ * у0 если х\~' = Р, х$ = г{, если х}~' =! А.
Типичной стратегией является стратегия как ты, так и я, а именно (Р; Р, А). После того, как каждый игрок выбрал стратегию {х{\ yt, z{), единственным образом определяется последовательность х, ..., х*, ... и средний выигрыш (12). Следовательно, возникает следующая биматричная игра (8x8)j
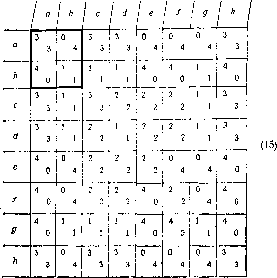
Здесь Ркраткая запись чисто мирной стратегии (Р; Р, Р). Аналогично А = (А; А, А) обозначает чисто агрессивную стратегию. Следовательно, северо-западная 2x2 подматрица (15) является собственно матрицей игры дилемма заключенного.
Отметим, что для удобства вычислений мы слегка изменили числа по сравнению с примером 1 гл. I (см. упр.
4 ниже).
При цикличности последовательности (х*) вектор выигрышей является средним арифметическим соответствующих элементов исходной матрицы 2x2. При этом возможны три варианта:
1) (Р, А) {А, Р)(Р, А)..... например (Р; Р, А) против
(А; Р, А);
2) (Р, Р) (Р, А) {А, А) (А, Р) (Р, Р), .... например (xt; Р, А) против (х2; А, Р) для всех хг, х3;
3) (Р, Р)(А, А)(Р, Р), например (Р; А, Р) против
(Р; а, р).
Во всех других случаях последовательность (х1) становится стационарной после некоторого конечного числа ходов, и соответствующий выигрыш является чистым.
В приведенной выше биматричной игре (8x8) две стратегии каждого игрока сразу же могут быть вычеркнуты, а именно (Р; А, А) кгк эквивалентная А и (Л; Р, Р) как эквивалентная Р.
Таким образом, останется игра (6x6) с двумя равновесными по Нэпу исходами, а именно (Л, Л) (некооперативное равновесие исходной игры) и (Р; Р, Л) (Р; Р, Л) новый NE-исход, в котором оба игрока применяют стратегию как ты, так и я. Интерпретация этого специфического устойчивого соглашения в повторяющейся игре в точности аналогична интерпретации сценария предостережений в примере 1.
Заметим, что в игре (15) стратегия Р (мирная) не доминируется больше стратегией Л (агрессивной). Однако после последовательного исключения доминируемых стратегий мирная стратегия в конце концов окажется отброшенной.
Оптимальный по Парето І?Е-исход (т. е. применение стратегии как ты, так и я обоими игроками) является исходом сложного равновесия игры (15).
Упражнение 4
Докажите, что игра (15) разрешима по доминированию и сложному равновесию соответствует выигрыш (3, 3). Сохранится ли этот результат, если исходная игра будет иметь структуру игры дилемма заключенного, но трем предельным циклам будут соответствовать различные средние выигрыши?
4. КЛАССИФИКАЦИЯ ИГР ДВУХ ЛИЦ
В этом разделе мы ограничимся рассмотрением игр двух лиц. Для таких игр a-ядро совпадает со множеством дележей, а P-ядро и у-ядро (определение 5) являются его подмножествами, причем по крайней мере одно из них непусто (теорема 1).
С этих пор мы предполагаем заданной игру двух лиц G = *= (Х1( Х„ ult и2) с конечными множествами стратегий Xlt Х3 (хотя большинство результатов, приведенных ниже, остается справедливым и для компактов Х( и непрерывных функций и„ t=l, 2).
Лемма 5, а -ядро игры G совпадает со множеством всех дележей
C(G)^/(G).
Р-ядро игры G задается условиями:
( вектор х* оптимален по Парето,** € Ср (G) ф і inf sup и, (у{, (/,),(**), /= 1, 2.I !/i /
Доказательство немедленно следует из определений 3 и 4 И поэтому будет опущено. Отметим, что P-ядро G может быть пустым: рассмотрите, например, игру двух лиц с нулевой сум* мой, не имеющую цены.
Пример 5. Модифицированная координационная игра Два игрока выбирают натуральное число из множества {1, 2, .... 10}.
Пусть выбраны xt, х2 и х1 + х2=10, тогда выигрыш игрока і равен xt. В оставшихся случаях платежный вектор равен (4, 0), если х1-\-х2 четно, и (0, 4), если хг + х2 нечетно. Гарантированный выигрыш игрока i sup inf и{ равенхі х/
Нулю, т. е. совпадает с минимальным возможным выигрышем. Дележи являются оптимальными по Парето исходами, т. е. для них выполнено х1 + х2=Ю.
Тем не менее inf sup и,-= 4, і1, 2, поэтому из леммы 4х/ хі
Следует, что (3-ядро состоит только из трех исходов (4, 6) (5, 5) (6, 4).
Для того чтобы стабилизировать с помощью предостерегающих угроз дележ (2, 8), необходимо, чтобы оба игрока согласились на выбор стратегий в открытую. В противоположность этому реализация дележа из (3-ядра требует более слабого информационного ограничения: нужен лишь сигнал, информирующий игрока об отклонении его партнера. С другой стороны, во многих играх двух лиц a-ядро и (3-ядро совпадают. В частности, это верно для смешанного расширения, поскольку обе игры с нулевой суммой (М„ М2, ых) и (М?
М2, й2) имеют цену.
Рассмотрим подмножество таких дележей, которые могут быть стабилизированы парой предупреждений, т. е. парой угроз, совпадающих с наилучшими ответами игроков.
Определение 5. у-ядро игры G состоит из таких дележей х*, для которых существует сценарий предостережений (х*, ?„),
где угрозы 1;, і=1, 2, суть предупреждения:
Г Uj (хр І; (Xj)) Uj (.x*),
УХ/фх,- j u, (X.y ^ (*,))= sup Ui(xj, Xi).
\ xieXi
Будем использовать обозначение Cy(G) для у-ядра.
Лемма 6. Предположим, что функция ut взаимно однозначная, і=1, 2. Напомним, что S{ обозначает і-выигрыш по Щтакельбергу
S; = sup{M,(x,, xj) I (Xj, X,) € BR,} i = 1, 2,
где BR,множество наилучших ответов игрока j (см. гл. II, разд.
4).
Тогда у-ядро игры G состоит из таких оптимальных по Парето исходов х, для которых
і=1, 2. (16)
Доказательство. Предположим, что я*оптимум Парето, удовлетворяющий (16). Для любого х,фхf обозначим через Xj~\j(xi) наилучший ответ игрока /. ГІо определению S{ имеем
,(*.- ^(x.))S,Mf(x^), І== 1, 2, х{ Фxf.
Следовательно, (я*, g2) является сценарием предостережений, а поэтому исходя* индивидуально рационален (по лемме 1; мы можем также утверждать справедливость неравенства sup inf w; ^ Sj). Таким образом, исход я* является дележом,*1 *7поскольку по предположению он оптимален по Парето.
Докажем обратное утверждение. Пусть я* принадлежит у-ядру игры G. Тогда существует сценарий предостережений (х*, Іг, У, в котором %i(Xj)(единственная в силу предположения о взаимной однозначности) стратегия наилучшего ответа игрока і на яу. Докажем, что я* удовлетворяет (16).
Выберем сначала я, Ф х*. По свойству имеем
щ(х{, ?,(**)
Осталось доказать, что
х, = I, (X*) = и, (xf, х}) щ (я*).
Предположим противное:
щ (я*) щ {xf, xf).
В силу оптимальности по Парето исхода я* получаем sup Uf (я,*, yf) = Uf {xf, Xf) Uf (я*).4f
Полученное противоречие доказывает лемму.
Замечание. Предположение о взаимной однозначности может быть опущено в формулировке леммы 6, если Sf заменить нау, sup inf щ(х{, x,)).X і XjbBRji X;)
Доказательство аналогично предыдущему и оставляется читателю в качестве упражнения.
Предупреждение предполагает выбор игроками своих наилучших ответов и, следовательно, является весьма правдоподобной угрозой. Характерным примером может служить угроза как ты, так и я в игре дилемма заключенного ((1) в примере 1). В противоположность этому любая стабилизирующая угроза, которая отличается от предупреждения, имеет черты запугивания, а именно: Если ты отклонишься, то я пожертвую своими краткосрочными интересами, чтобы наказать тебя и тем самым обеспечить долгосрочную стабильность кооперации.
В работе Шеллинг [1971] содержится замечательный пример такого сорта. В этом примере речь идет об индусском монахе, который без всякого оружия охранял в пути драгоценности одной лишь угрозой покончить с собой, если эти драгоценности будут украдены.
Традиции моральной стойкости оказалось достаточно для убедительности этой угрозы.
Лемма 6 устанавливает связь между осуществимостью стабильности с помощью предупреждений и борьбой за лидерство (гл. Ill, разд. 1.) Она утверждает, что в игре G возникает борьба за лидерство в том и только в том случае, если ее у-ядро пусто.
Таким образом, в игре с пустым у-ядром стабильности любого дележа угрожает возможность захвата лидерства одним из игроков. Вместе с тем, другой игрок в этом случае может использовать угрозу типа машины страшного суда.
Правдоподобность успеха той и другой тактики с точки зрения стороннего наблюдателя конфликта одинакова.
Пример 6. Дуополия с назначением выпуска
Рассмотрим дуопольную игру, аналогичную игре, рассматриваемой в примере 5 гл. III. Две фирмы поставляют некото рый товар на рынок, /-я фирма предлагает товар в объеме xh і'=1, 2. Цена на товар определяется формулой р0(х1 + хг) (для X!-l-x2^p0).
Функции затрат одинаковы у обеих фирм, причем затраты на выпуск единицы продукции линейны относительно количества выпускаемого товара. Затраты на выпуск единицы продукции при увеличении масштабов производства могут быть как возрастающими, так и убывающими.
Хі = Х2 = [0, у/о] ,
?(*!, *а) = 0 х\х{ (c-i-eXi) xt, t=l, 2,
где х х, + х2, а ра, с, ефиксированные параметры, удовлетворяющие условию
О у/70 с /?0.
Предполагается, что е мало по сравнению с р0с.
Случай 1. Постоянные затраты на выпуск единицы продукции Заметим, что
И- и\ [/?„х\хсх хг + (Ро с) х, следовательно, исходы х, такие, что
х ~ ~2 (Ро с)*
являются оптимальными по Парето. Верно и обратное утверждение, т. е. все оптимальные по Парето исходы удовлетворяют условию x = -j(Poс).
Проверку этого утверждения предоставляем читателю ^нужно приравнять нулю определитель матрицы Ь (л;1’ "2 ) ' ^аксимальныи общий доход равен у-(р0с)2.
Гарантированный выигрыш равен 0 (поскольку supinf=\ *1 *2
= sup и] у Po'j'j- Таким образом, дележи представляют
собой произвольное распределение максимального суммарного дохода (при условии, что не получается отрицательных выигрышей). Для вычисления выигрышей по Штакельбергу нам понадобится вычислить наилучший ответ игрока 1:
BR х (х2) = у (р0 с) ^ хг.
Таким образом,
y2 = S2 = sup ul (BR1 (x2), x2) =
0 Xi p0
- sup y[(Poс)хг x22]=S2 (pac)2.
0 * у Po
Симметричными рассуждениями получаем Sj y-(/?0с)2, следовательно, вектор выигрышей (S,, S2) соответствует некотощего максимальный суммарный доход поровну мржду игроками. В этой симметричной игре у-ядро является справедливым кооперативным исходом, реализующим с помощью естественных угроз BRit BR2. Реализация любого несправедливого распределения максимального общего дохода требует применения тактики запугивания.
Такие угрозы выглядят менее убедительно.
Случай 2. Возрастающие или убывающие (е Ф 0) затраты на выпуск единицы продукции
С помощью аналогичных вычислений, использующих аппроксимацию первого порядка (возможную в силу малости е), получаем
Si (е) = S2 (е) ~ -g {pcf (1 + Зв).
Предположим сначала, что е 0. По определению функции и\ имееми? (х) и\ (х) для всех хг 0, х2 0.
Отсюда получаем, что вектор выигрышей (S, (0), S2 (0)), соответствующий некоторому дележу в игре G, не является допустимым в игре G (е), е 0. Тем более вектор выигрышей (S, (е), S2 (е)) не является допустимым, и у-ядро игры G (е) пусто. Аналогичные рассуждения (с учетом S{ (е) S{ (0) и и? и1- для е 0) показывают, что у-ядро игры G (е) непусто при убывающих затратах на выпуск единицы продукции (е 0).
Рисунок 1 показывает разницу между случаями убывающих и возрастающих затрат на единицу выпуска.
е 0 убывающие затраты на единицу выпуска
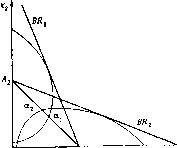
-ядро есть [а1( а2] Кривые линии определяются условием8 О
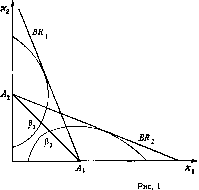
7-ядро пусто на [Рі, Р2] оба игрока используют угрозы типа запугивания.
Упражнение 5
Докажите, что в модифицированной координационной игре (пример 5) множество {ut (х) О S,} пусто. Тем не менее у-ядро не пусто (здесь нужно воспользоваться замечанием 2).
Покажите, что у-ядро состоит из единственного дележа (5, 5), который является справедливым исходом игры.
Упражнение 6
Предположим, что -{ гильбертова норма в ^(порожденная положительно определенной симметричной матрицей 2x2) и і'=1, 2, фиксированы. Рассмотрим игру
f X^X.^R,
I и,{ (х) = II х cLf (I ? 1, 2.
Покажите аналитически и геометрически, что у-ядро не пусто.
Из леммы 6 следует, что у-ядро данной игры G пусто в том (и только том) случае, если в этой игре возникает борьба за лидерство. Из леммы 4 получаем, что (3-ядро игры G пусто тогда (и только тогда), когда вектор выигрышей 3 = (inf sup ut, inf sup u2)
Уг Уі Уі Уг
не является допустимым (т. е. не существует исхода х, для которого было бы выполнено неравенство (3 ^ (ut (х), и2 (%)). Действуя в качестве ведомого, игрок і гарантирует себе результат inf sup щ (поскольку перед выбором у{ он знает у}). ТакимУ; Уіобразом, пустота (3-ядра порождает „борьбу за право второго хода": какой бы дележ ни был выбран, по крайней мере одномуигроку выгоднее подождать пока будет окончательно определена стратегия его партнера, а затем действовать в качестве ведомого:
Vxg Х{і2} Зі € {1, 2} и, (дс) inf sup и,-.
и, Ц
Как показывает следующий результат, эта терминология является корректной, борьба за лидерство (право первого хода) и борьба за право второго хода не могут возникнуть одновременно.
Теорема 1. у-ядро и fi-ядро не могут быть пусты одновременно.
Если у-ядро и fi-ядро не пусты, то они пересекаются.
Следствие. Игры двух лиц распадаются на три класса:
I. Ср = Ф, Су Ф ф: борьба за право второго хода,
II. Су = Ф, Ср Ф ф: борьба за лидерство,
Ш. СрПСуФФ: в этом случае Ср П С? является благоприятной областью для кооперации с использованием угроз.
Доказательство. Пусть х{, і = 1, 2, равновесие по Шта-кельбергу, в котором игрок і является лидером.
Пусть Dt - Множество исходов, удовлетворяющих следующим неравенствам!
Уі Щ (х), р, и, (х).
Поскольку x*j является наилучшим ответом игрока ] на х\, то множество Dt содержит х‘ и поэтому не пусто.
Предположим теперь, что у-ядро и P-ядро пусты. Выберем оптимальный по Парето исход х из Д (например, максимизируя иг-\-щ на Вг). Тогда имеем
Cv(G) = 0±m2(х) у2,
C/3(G) = 0=M*) Pi-
Поскольку хг принадлежит D$, заключаем, что исход хі доминирует по Парето исход х. Получили противоречие.
Предположим теперь, что у-ядро и P-ядро не пусты и докажем, что их пересечение также не пусто. Положим у = (у1( Уа).
Если у^р, то CgcrCy, и все доказано. Аналогично, если Р^у, то Cpf]Cy = Cv. Осталось рассмотреть случаи типа
Рі ^ Ук Уі ^ Pa-
Тогда любой дележ из Dlt например х1, принадлежит Cv f) Ср. Характерным примером игр класса I являются игры с нулевой суммой без цены.
На самом деле игра класса I не имеет равновесий по Нэшу.
Упражнение 7
Если P-ядро игры G пусто, то NE (G) также пусто, и игры е нулевой суммой (Xj, Х2, uj и (Хи Х2, и2) не имеют цены.
Примером игр класса II является игра „перекресток (пример 2 гл. III).
Упражнение 8
Для игры G из класса II выполнено Р/?і- ' = 1.2.
Для любой игры класса III пересечение CvfCp является подходящей областью для кооперации с помощью угроз). Ниже приведены два упражнения и задача.
Они показывают, что типичными примерами игр класса III могут служить игры, имеющие равновесие в доминирующих стратегиях, а также игры с оптимальным по Парето вектором у или (5, как это имеет место в следующих двух упражнениях и задаче.
Упражнение 9
Пусть каждый игрок имеет строго доминирующую стратегию, т. е.
и, (х*, И; (xh Xj) для всех х{ф х? и для всех xJt
тогда игра G принадлежит классу III. Приведите пример, показывающий, что игра G, в которой каждый игрок имеет доминирующую стратегию, может принадлежать классу II.
Упражнение 10
Игра G, для которой вектор у является вектором выигрышей по крайней мере для одного дележа, принадлежит классу III.
Задача 4. Квазинесущественные игры
Скажем, что игра G является квазинесущественной, если р = (inf sup и1( inf sup и2) является вектором выигрышей по
У: У\ Уі Уг
крайней мере для одного оптимального по Парето исхода.
1) Предположим, что функции и1У и2 взаимно однозначны на Х{і2} и что игра G квазинесущественна, Тогда (единственный) исхода;*', для которого (ыДх*), 2(х*)) = Р, является і-равнове-сием по Штакельбергу для /= 1, 2. Этот дележ также является единственным Л^-исходом игры G.
2) Приведите пример квазинесущественной игры, в которой нет /Vf-исхода.
3) Предположим, что игра G квазинесущественна. Докажите, что игра G несущественна в том и только том случае, если игры с нулевой суммой (X,, Х2, ых) и (Хх, Х2, иг) имеют цену.
Приведите пример квазинесущественной игры, не являющейся несущественной, в которой функции и{, І = І, 2, взаимнооднозначны.
Задача 5. Сценарий гарантированных предостережений (Мулен [1977])
Пусть (х*, gj, g2) сценарий предостережений игры G. Назовем угрозу гарантированной, если ее реализация не приносит убытков угрожающему игроку;
ДЛЯ любых Xj, Xj.
(*іі (*і)) ^ (- *¦*) ^ (Іі (%г)і \
и2 (lj (х2), х2) ^ и2 (х*) ^ Ц2 (Xj, ^2 (^і))- I
g-ядром игры G является подмножество, обозначаемое Cg (G), таких исходов х*, для которых существует по крайней *мере один гарантированный сценарий предостережений (х*, х, 2).
1) Докажите следующую эквивалентность:
х€Сг(0)ФФ[х оптимален по Парето и и;(х)^(ЗД
2) Докажите, что g-ядро является подмножеством, возможно пустым, у-ядра:
Cg(G)czCy (G).
3) Приведите примеры игр нз класса I, показывающие, что g-ядро может быть как пустым, так и непустым.
Указание: рассмотрите следующую игру 2x2:и опишите необязательные соглашения в этой игре (включая смешанные Nf-исходЫ и равновесия в совместных смешанных стратегиях).
4) Для игры G, принадлежащей классу III, докажите, что либо ее g-ядро пусто, либо игра G квазинесущественна (задача 4). В последнем случае докажите, что
Cf = Cv = C =(ult 2Г1(Р).
5. ИГРЫ В ХАРАКТЕРИСТИЧЕСКОЙ ФОРМЕ: ЯДРО
Пример 7. Игра „джаз-оркестр" (Янг [1979])
Владелец ночного клуба в Париже обещает 1000 долларов певцу (S), пианисту (Р) и ударнику (D) за совместную игру в его клубе. Выступление дуэта певца и пианиста он расценивает в 800 долларов, ударника и пианиста в 650 долларов и одного пианистав 300 долларов. Другие дуэты и солисты не рассматриваются, поскольку присутствие фортепиано владелец клуба считает обязательным. Дуэт певецударник зарабатывает 500 долларов за вечер в одной удобно расположенной станции метро, певец зарабатывает в среднем 200 долларов за вечер в открытом кафе.
Ударник один ничего не может зара-ботать.
Суммарный доход трех музыкантов максимален (1000) в случае их совместного выступления в ночном клубе. Если певец выступает отдельно от пианиста с ударником, то все втроем они получают 650 -f 200 долларов, если пианист один выступает в ночном клубе, то 300-{-500 долларов.
Наконец, суммарный доход равен 800 долларов, если пианист и певец отказываются от участия ударника. Какое распределение максимального общего дохода следует признать разумным, учитывая описанные возможности игроков в смысле частичной кооперации и индивидуального поведения?
Определение 6. Для данного конечного сообщества N игрой в N -характеристической форме назовем отображение ? из множества непустых коалиций игроков Р (N) в R. Игра (N, ?) называется супераддитивной, если для любых неперееекающихся коалиций Т, S g Р (N) выполнено
v(T) + o(S)^v(T[}S). (17)
Свойство супераддитивности (условие (17)) не является необходимым для большинства результатов, приведенных ниже, однако оно необходимо для интерпретации числа ? (Т) как максимального общего дохода в случае, когда игроки в коалиции Т действуют независимо от дополнительной коалиции Те. Неравенство (17) означает, что коалиция Tl)S имеет не меньше возможностей, чем две независимые непересекающиеся коалиции Т и S,
Из супер аддитивности ? с очевидностью следует, что для любого разбиения Slt ..., Sk множества N выполнено2 v(Sk)^v(N). (18)fe= 1
Следовательно, не существует такого разбиения Sx, .... Sk, которому бы соответствовал суммарный доход, превышающий доход коалиции всех игроков v(N).
Таким образом, кооперация всех игроков является единственным эффективным кооперативным исходом.
Замечание 1. В определении 1 предполагается, что исход кооперации может быть выражен в одних и тех же единицах измерения, т. е.' существует трансферабельный товар, на основе которого могут быть осуществлены побочные платежи между игроками.