Классификация моделей итеративного научения человека
Первый аспект - результативный - при научении система должна достичь требуемого результата - качества выполнения действий с приемлемыми затратами времени, энергии и т.д. Второй аспект - процессуальный: адаптация, приспособление научаемой системы к некоторому виду действий в процессе упражнения и т.д.
Соответственно, выделяют результативные характеристики итеративного научения и характеристики адаптации [57]. В настоящей работе речь идет именно о результативных характеристиках научения (характеристики адаптации зачастую имеют совсем другую динамику).
В случае итеративного научения можно считать, что на его результативные характеристики влияют две входные переменные -информация о значении выходной переменной и параметры окружающей среды - внешние условия. Если бы на каком-то шаге изменились оба значения входных переменных, то результаты научения на этом шаге и на предыдущем были бы просто несравнимыми - нельзя было бы сказать почему реализовалось именно такое значение выходной переменной: потому, что обучаемая система повела себя соответствующим образом, или потому, что изменились условия ее функционирования. Поэтому постоянство внешних условий является существенной характеристикой ИН.
Для сравнимости результатов научения в различные моменты времени (использование количественного описания), даже при постоянных внешних условиях, важно также постоянство цели научения.
В качестве основной результативной характеристики ИН обычно принимается критерий уровня научения. При обучении реальных систем в качестве критерия уровня научения могут выступать следующие характеристики [56]:
- временные (время выполнения действия, операции, время реакции, время, затрачиваемое на исправление ошибки, и т.д.);
- скоростные (производительность труда, скорость реакции, движения и т.д. - величины, обратные времени);
- точностные (величина ошибки в мерах физических величин (миллиметрах, углах и т.п.), количество ошибок, вероятность ошибки, вероятность точной реакции, действия и т.д.);
- информационные (объем заучиваемого материала, перерабатываемой информации, объем восприятия и т.д.).
Так как ниже рассматриваются в основном модели именно итеративного научения, то будем для общности изложения называть интересующую нас результативную характеристику научения рассогласованием. Действительно, во всех перечисленных выше случаях мы имеем либо функцию ошибки (рассогласования), либо характеристику наученности системы, которая может быть сведена к некоторой функции ошибки.
Например, время выполнения действия может интерпретироваться как рассогласование, если под последним понимать разность между текущим значением времени выполнения действия и минимально возможным.
Как отмечалось выше, итеративное научение, как правило, характеризуется замедленно-асимптотическими кривыми научения, аппроксимируемыми экспоненциальными кривыми. В общем виде экспоненциальная кривая описывается зависимостью (2.1) x(t) = x? + (x0 -1") e ~7\ t 0, или последовательностью
xn = x? + (x0 - x") e ~7n, n = 0, 1, 2, .. , m, где t - время научения, n - число итераций (проб, попыток) с момента начала научения (предполагается, что научение начинается в нулевой момент времени), x(t) (xn) - значение рассогласования в момент времени t (на n-ой итерации), x0 - начальное значение рассогласования (соответствующее моменту начала научения), x? -конечное значение рассогласования (величина, к которой КН асимптотически стремится; как правило, в биологических системах эта величина рассматривается как физиологический предел науче-
ния), g - некоторая неотрицательная константа, определяющая скорость изменения КН и называемая скоростью научения (g имеет размерность обратную времени или числу итераций). Эскизы графиков кривых (2.1) приведены на рисунках 2.1.а и 2.1.б.
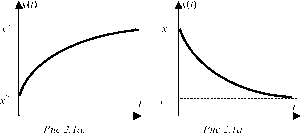
(2.2) x(f) = e - g ‘
(2.3) x(f) = 1 - e - g 1 .
Если речь идет о величине ошибки, то в соответствии с(2.2), ошибка монотонно убывает. Если же x интерпретируется, например, как уровень наученности, то он, в соответствии с (2.3), монотонно возрастает. Очевидно, что (2.2) и (2.3) могут быть получены из общей зависимости (2.1) с помощью линейного преобразования:
(2.1)
x(2.3)
x -x
x(22) = 5--
x - x
Поэтому, говоря о кривой научения, мы будем подразумевать семейство кривых, эквивалентных с точностью до линейного преобразования. Характеристикой семейства - величиной, одинаковой для всех КН из рассматриваемого класса эквивалентности, в этом случае будет скорость научения.
Эскизы графиков зависимостей (2.2) и (2.3) приведены на рисунках 2.2.а и 2.2.б, соответственно.
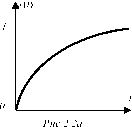
где a, ft - некоторые константы. По аналогии с мономолекулярной автокаталитической реакцией или с использованием аналогий с химическим законом действующих масс [99]: x(t) = a e 7 t / (b + e 7 %
Thurstone L. на основании обобщения экспериментального материала Lashley K. (обучение крыс нахождению пути в лабиринте) предложил аппроксимировать накопленную ошибку (то есть суммарную ошибку, начиная с нулевого момента времени или первой итерации) следующей формулой:
(2.4) x(n) = a n / (b + n),
где n - число упражнений, a, Ь - некоторые положительные константы [114].
Предложенное H. Gulliksen в [101] эмпирическое уравнение КН для накопленных ошибок при предельном переходе (достаточно малой скорости научения и силе подкрепления) переходит в (2.1), то есть КН приближается экспонентой.
Усредненная КН, полученная Р. Аткинсоном и коллегами [13 и др.] в соответствии с теорией отбора стимулов, близка к показательной функции.
Следует отметить, что во многих работах указывалось на необходимость исследования усредненных (по испытуемым - их группе, или по времени) кривых научения, так как индивидуальные КН имеют, как правило, значительный разброс (... гладкие КН - результат процесса усреднения ... [99, с. 392]) [102, 106].
В работе [73] для описания количественной взаимосвязи факторов подкрепления, неподкрепления и условной реакции в экспериментах по формированию условных рефлексов была предложена формула вида (2.4) (для зависимости уровня сформированности условного рефлекса от количества подкреплений условного раздражителя).
Для аппроксимации экспериментальных кривых научения различными исследователями использовались экспоненциальные функции, гиперболы, параболы и др. [69]. Различались КН с возрастающим, убывающим и постоянным приростом [75].
Откладывая обсуждение разнообразия подходов, отметим, что при сравнении тех или иных описаний ИН необходимо, в первую очередь, обращать внимание на то, является ли это научение итеративным, какие показатели анализируются в качестве характеристик эффективности научения и в какой шкале эти показатели измеряются.
Так как итеративное научение является одним из частных случаев научения, то, помимо экспоненциальных кривых, соответствующих итеративному научению, встречаются КН других типов, в том числе - логистические КН.
Логистические кривые научения аппроксимируются зависимостью
(2.5) x(t) = x0 x?/ (x0+ (x? - x0) e ~7%
и в зависимости от соотношения начального и конечного значений рассогласования могут быть как возрастающими, так и убывающими [113]. Эскиз графика нормированной возрастающей логистической кривой приведен на рисунке 2.3.
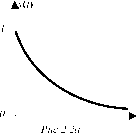
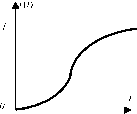
При сравнительно сложных видах научения КН может иметь плато, наличие которого объясняется скрытыми поисками обучаемой системой новых путей совершенствования способов выполнения действий, подготовке к переходу на качественно новый способ овладения деятельностью, к новой стратегии [27, 98, 102]. На рисунке 2.4. приведен достаточно распространенный тип КН с промежуточным плато: две последовательные экспоненты соответствуют отработке двух различных стратегий действий.
Несколько начальных проб может быть потрачено на поиск наиболее целесообразной тактики поведения, что приводит к наличию начального плато на логистической кривой [57]. В сложных процессах обучения, в соответствии с [23], можно выделить три стадии. Первая стадия характеризуется отбором из большого числа раздражителей значимых раздражителей.
Эту стадию можно рассматривать как формирование исходного поля событий. Вторая стадия характеризуется выработкой правильного поведения, обусловливаемого отобранной системой событий (собственно итеративное научение - именно вторая стадия).
Третья стадия характеризуется относительно стационарным уровнем обученности.
И, наконец, при использовании дихотомических шкал(когда произвольно устанавливается какой-то критический уровень ошибки; если в процессе выполнения действия величина ошибки меньше критического значения, то действие считается выполненным правильно) или выборе в качестве критерия уровня научения обратных для времени, точности выполнения действия и объема перерабатываемой информации величин, то есть при использовании дивизорного преобразования (скорость реакции, производительность труда и др. - как величины, обратные времени и т.д.), могут встречаться логистические кривые. В этом случае их появление несколько неестественно и может быть устранено выбором соответствующих шкалы и единиц измерения.
Можно показать, что, строя для экспоненциальной кривой обратную или производя дискретизацию шкалы, можно получить логистическую КН [56, 111]. Кривые научения, соответствующие нерезультативным характеристикам научения в том числе и итеративного, то есть характеристики адаптации, могут представлять собой комбинации экспоненциальных и логистических КН, ступенеобразные, или любые другие, в том числе и немонотонные кривые. Такие КН, характеризующие внутреннюю структуру действий, в том числе, например, при формировании разнообразных навыков у человека и животных, могут наблюдаться в сложных видах научения: при последовательной глубокой перестройке структуры навыка, организации поэтапной отработки отдельных компонент действий и т.д. [57].
В дальнейшем мы будем рассматривать кривые научения, соответствующие только результативным характеристикам итеративного научения.
Закономерность итеративного научения (как наиболее простого вида научения вообще), заключающаяся в замедленноасимптотическом виде кривых научения, соответствующих результативным характеристикам ИН, свидетельствует о наличии общих механизмов научения у объектов живой природы - человека, групп людей, животных и их искусственных аналогов - технических и кибернетических систем. Не приводя подробных экспериментальных данных - они содержатся в цитируемой литературе, ниже мы попытаемся, анализируя математические модели ИН, выяснить, что же лежит в основе этих общих закономерностей.
Классификация моделей итеративного научения человека, животных и искусственных систем
Большинство моделей итеративного научения строится на основе аналогий с явлениями и процессами, происходящими в тех или иных системах живой или неживой природы. Поэтому в основание классификации естественно положить тип процесса или явления, аналогия с которым используется.
На рисунке 3.1 приведена предлагаемая система классификаций моделей итеративного научения.
В описательных моделях (аксиоматических и интуитивных) вводятся (постулируются) те или иные предположения о связи переменных и параметров системы, причем эти предположения и модель обучаемой системы, как правило, достаточно абстрактны и не апеллируют к реальным аналогам (в интуитивных моделях они основываются на интуиции и здравом смысле). Этот класс моделей рассматривается в разделе 4 настоящей работы.
Раздел 5 посвящен описанию моделей ИН, использующих аналогии с положениями физических явлений и принципами функционирования технических систем. Их подкласс - теоретикоинформационные модели - вынесен в отдельный раздел в силу своей специфики и разнообразия (раздел 6).
Модели, использующие аналогии кибернетических систем, -раздел 7 и модели коллективного поведения - раздел 8, интересны тем, что это - искусственные, достаточно абстрактные модели, причем те системы, по аналогии с которыми они строятся, зачастую, в свою очередь являются моделями некоторых реальных систем (модели - аналогии моделей).
Так как используемые аналогии достаточно разнообразны, мы попытаемся вести изложение на максимально обобщенном уровне, конкретизируя значения тех или иных терминов лишь тогда, когда это будет необходимо для предотвращения неоднозначности понимания. Приведем общую структуру описания математической модели итеративного научения.
Предположим, что обучаемая система (далее - просто система) состоит из п, в общем случае взаимодействующих, элементов (п 1), каждый из которых описывается некоторым скалярным параметром х(), зависящим от времени, который мы будем в дальнейшем условно называть рассогласованием /-го элемента. Рассогласование системы x(t) каким-то образом зависит от рассогласований составляющих ее элементов:
x(t) = F(x;(0, х2(0, Хп(0).
Такое описание является общим для большинства моделей, которые также - предположениями о взаимодействии элементов (функции F(-)).
Все изложение приводимых ниже моделей строится по следующей схеме (некоторые из этапов могут быть опущены или различаются содержательными интерпретациями терминов система, элемент, параметр, рассогласование и т.д., а объединены с другими):
- описание модели (О) - язык описания, предметная область, факторы и переменные;
- гипотеза (Г) - предположения о связи переменных, механизмах взаимодействия и т.д.;
- формальные (логические, алгебраические и др.) преобразования (Ф);
- вывод (В) (вывод из результатов анализа большинства приводимых ниже моделей - рассогласование описывается зависимостью следующего вида ... , причем зависимость эта, как правило, экспоненциальная);
- анализ модели (А) - обсуждение гипотезы, предположений, их обоснованности, исследование факторов, влияющих на скорость научения, и т.д.
Скорость научения, в общем случае, зависит от всех параметров модели: числа элементов, связей и законов их взаимодействия. Знание вида этой зависимости представляется достаточно важным, так как исследование параметров, определяющих скорость научения, существенно для поиска путей повышения эффективности научения и, в первую очередь, самой скорости научения.
Действительно, зная зависимость скорости научения от параметров модели, можно предложить меры, приводящие к соответствующему изменению этих параметров, и, следовательно, требуемому изменению (чаще всего увеличению) скорости научения.
Описание моделей, не принадлежащих автору настоящей работы, сопровождается ссылками на соответствующие источники (см. список литературы). В таких моделях изложение, за исключением этапа А - анализ, следует оригиналу - работам авторов моделей.
Следует признать, что в целях унифицированности и простоты изложения автору пришлось допустить ряд вольностей, которые могут вызвать справедливые возражения читателя-математика. Так, например, иногда идентифицируются разностные и дифференциальные уравнения и приводятся утверждения о соответствии между их решениями.
В последнем случае в моделях с дискретным временем под экспоненциальной кривой мы будем понимать последовательность значений критерия уровня научения, элементы которой составляют геометрическую прогрессию.
Завершение описания каждой модели отмечено значком - .
Описательные модели: аксиоматика и интуиция
Под описательными мы будем понимать модели итеративного научения, в которых явно не проводятся аналогии с принципами устройства и функционирования тех или иных систем, а экспоненциальный вид КН получается в результате введения достаточно абстрактных и не обосновываемых предположений относительно законов и правил взаимодействия элементов обучаемой системы (в аксиоматических моделях иногда постулируется непосредственно, что кривая научения описывается экспонентой - выражением (2.1)). В большинстве случаев в описательных моделях вводимые предположения опираются на интуицию и апеллируют к здравому смыслу, а выводы из анализа динамики КН зачастую лежат в основе моделей более высокого уровня [14, 31].
Модель 4.1.
О. Изменение рассогласования системы во времени.
Г(В,Ф). Скорость изменения рассогласования пропорциональна его текущему значению, причем коэффициент пропорциональности не зависит от времени. То есть
(4.1)
g x(t).
dx(t) dt
Вывод очевиден - решением этого дифференциального уравнения является экспонента - выражение (2.1).
А. Значительная часть аксиоматических моделей так или иначе предполагает пропорциональность между изменением рассогласования в единицу времени и его текущим значением. Понятно, что при постоянном коэффициенте пропорциональности такое предположение сразу приводит к экспоненциальному виду КН, причем для увеличения скорости научения необходимо увеличивать величину коэффициента g который в дальнейшем в различных моделях будет интерпретироваться как количество информации, перерабатываемой обучаемой системой в единицу времени, пропускная способность канала связи, объективно существующее ограничение на скорость изменения параметров элементов и т.д.
Аналогичные построения (правда, при несколько более искусственных исходных гипотезах) приведены в [75]. В модели с дискретным временем, если: xn - xn-1 = - a xn, то
xn = (1 - a)n x0, n = 1, 2, ... ,
и скорость научения убывает с ростом a (а е (0; 1)). Если же xn = Ь xn-1, то xn = Ьn xa n = 1, 2, ... , и скорость научения возрастает с ростом Ь (Ь е (0; 1)). -
Модель 4.2. (Р. Буш, Ф. Мостеллер, У. Эстес [23, 43, 99, 106]).
О. Рассогласование - вероятность правильной реакции (например, в известном эксперименте крыса в лабиринте) [13, 23, 79 и др.]. Исследуется зависимость рассогласования от числа повторений.
Если вероятность правильной реакции равна р (вероятность неправильной реакции равна, соответственно, (1 - p)), то она может увеличиться не более, чем на (1 - p), и стать равной единице, и уменьшиться не более, чем на р, и стать равной нулю.
Г. На каждом шаге прирост рассогласования пропорционален возможному приращению, а уменьшение пропорционально возможному уменьшению. Разностное уравнение для вероятности правильной реакции имеет вид:
(4.2) xn = xn-1 + an (1 - xn) - bn xn1, n = 1, 2, ... , где an, bn 0.
Ф(В). При начальной точке x0 и постоянных коэффициентах а (an = a), и b (bn = b) получаем
xn = xo (1 - а - b)n + а ^ (1 - а - b)k .
к=0
Непрерывный аналог этого решения имеет вид x(t) = x" + (x0 - x") e - (а + b) \
где x" = а / (а + b).
А. По сравнению с предыдущей моделью, в рассматриваемой здесь модели введено усложнение - возможность как увеличения, так и уменьшения рассогласования (ср. (4.1) и(4.2)), хотя, по сути, рассматриваемая модель является вероятностной модификацией модели 4.1. Постоянство коэффициентов приводит к экспоненци-альности решения, а скорость научения g = а + b, по-прежнему, определяется величиной коэффициентов а и Д
Статистическим моделям научения посвящено значительное число работ, особенно зарубежных авторов. В большинстве из них ИН понимается именно как ... систематическое изменение вероятности реакции [99, с. 395]. Приведем один из наборов требований к статистическим моделям:
1. Динамика усредненного показателя научения описывается кривой, имеющей отрицательное ускорение в своей конечной фазе и стремящейся к некоторой постоянной асимптоте (отметим, что в этом пункте требуется замедленная асимптотичность только в конечной фазе, то есть допускается, например, наличие начального плато - Д.Н.).
2. Гладкая кривая среднего является результатом усреднения ..., а асимптота наблюдаемой КН представляет лишь точку статистического равновесия [99, с. 397].
Следует отметить, что полученному решению уравнения (4.2) вполне соответствуют результаты экспериментов со многими животными (в большинстве случаев - с крысами) [23, 67], людьми [4, 100 и др.] и вероятностными автоматами [24 и др.].
Экспоненциальный вид КН обусловлен линейностью зависимостей (4.1) и (4.2) и постоянством (стационарностью) коэффициентов а и Д В следующей модели эта зависимость берется уже нелинейной. -
Модель 4.3. (Р. Буш, Ф. Мостеллер и др. [23]).
О. Изменение рассогласования (например, зависимость вероятности правильной реакции от числа повторений) системы во времени.
Г. На каждом шаге изменение рассогласования пропорционально текущему значению рассогласования и разности между некоторым конечным рассогласованием а и текущим. Динамика рассогласования удовлетворяет дифференциальному уравнению Бернулли
(4.3) = Ь x(t) (а - x(t)),
at
где а и Ь - некоторые константы.
Ф(В). При начальной точке x решением является логистическая кривая:
x(t) = ax0 / (x0 + (а - x0) e ~аb‘).
А. Наличие тормозящего довеска в (4.3) по сравнению с(4.1) и (4.2) приводит к тому, что КН получается не экспоненциальной, а логистической - появляется точка перегиба. Скорость научения, в отличие от предыдущих моделей, зависит не только от коэффициента пропорциональности между скоростью изменения рассогласования и текущим значением рассогласования, но и от величины конечного рассогласования. -
Модель 4.4. (К. Халл [36, 104, 105]).
О. Классической аксиоматической моделью итеративного научения является известная система постулатов К. Халла (C. Hull) для бихевиористской модели S-R-S (основой обучения является упрочение связей стимул-реакция).
Г(А, В). Закон формирования навыка (IV постулат) гласит, что, если подкрепления равномерно (равномерность проб - важная характеристика итеративного научения) следуют одно за другим, а все остальное (внешние условия и цели обучения) не меняется, то в результате прочность навыка х(п) будет увеличиваться с ростом числа испытаний согласно равенству:
Хп = 1 - 10 -g п.
А. Отметим, что кривая забывания согласно VIII постулату также является экспоненциальной кривой [105]. -
Модель 4.5. (Ю.Г. Антомонов [9, 11]).
О. Обобщенная модель обучения (например, обучение чело-века-оператора). Переменной является x - вероятность того, что у обучаемой системы сформировалась адекватная модель внешней среды.
Г. Из аналога принципа наименьшего действия (см. также модели раздела 5 настоящей работы) следует, что изменение вероятности удовлетворяет дифференциальному уравнению [11]:
(4.4) + a x(t) = Д dt
Отметим, что иногда уравнения типа (4.4) называются законом подкрепления статистической теории обучения. В [92] этот закон записывается в виде
Хп = Хп-і + a (1- Хп-і),
что соответствует ft = а (или (4.2) с Ь = 0, при этом если х0 = 0, то
х" = 1 [9]).
Ф(В, А) - см. модель 4.2. -
Многие исследователи изначально постулируют замедленноасимптотический вид КН и используют его в дальнейшем при количественном анализе, выработке различных рекомендаций и т.д. [75, 109, 115 и др.].
Практически во всех моделях настоящего раздела предполагается, что рассогласование системы удовлетворяет линейному дифференциальному уравнению с постоянными коэффициентами. При этом линейность и стационарность коэффициентов являются достаточными (но не необходимыми) условиями экспоненциаль-ности решения.
5. Модели - аналогии физических явлений и технических
систем
Рассматриваемые в настоящем разделе модели итеративного научения, предложенные разными авторами, опираются на аналогии физических явлений и принципов функционирования технических систем.