Специальные законы распределения
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 4X - 9Y + 5, если известны математические ожидания и дисперсии случайных величин X и Y:
| Номер зада ния |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| M (X) | 6,5 | 9,3 | 8,8 | 9,8 | 8,5 | 9 | 7,9 | 8,7 | 4,3 | 7,5 | 5,1 | 5,4 | 7,8 | 8,7 | 11 |
| M (Y) | 8,7 | 8,1 | 8,4 | 2,6 | 9,7 | 5 | 9,1 | 2,4 | 5,5 | 9,6 | 2,4 | 4,6 | 2,3 | 3,7 | 12 |
| D( X) | 0,5 | 0,9 | 0,3 | 1,4 | 1,3 | 3 | 1,1 | 1,2 | 0,3 | 0,6 | 0,8 | 0,2 | 0,9 | 0,6 | 3 |
| D(Y) | 0,4 | 0,5 | 0,3 | 1,2 | 2,2 | 4 | 4,5 | 0,3 | 0,8 | 0,2 | 0,5 | 0,7 | 1,3 | 1,8 | 8 |
Найти закон распределения этой случайной величины и её функцию распределения.
40. Дискретная случайная величина имеет два возможных значения x1 и x2, причем x1 x2.
Вероятность того, что случайная величина примет значение x1, равна 0,3. Найти закон распределения случайной величины, зная математическое ожидание M (X) = 4,8 и среднее квадратическое отклонение с( X) = 0,9.
41. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной в интервале (3;5) плотностью распределения f (x) = - 0,75x2 + 6x -11,25, а вне этого интервала плотностью распределения f (x) = 0.
42. Случайная величина Х задана плотностью распределения f (x) = 2cos x в интервале (0;п/4), а вне этого интервала f (x) = 0. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
43. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной в ин-тервале(2;4) плотностью распределения f (x) = -0,75x2 + 4,5x - 6, а вне этого интервала f (x) = 0.
44. Случайная величина Х задана плотностью распределения
f (x)
¦?Т
в интервале (-1; 1), а вне этого интервала f (x) = 0. Найти
п? 1 - x
моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
45. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной при x 0 плотностью распределения f (x) = xn 1e x /x0, а при x 0 плотно-
x0
стью распределения f (x) = 0.
46. Случайная величина Х в интервале (-3;3) задана плотностью
распределения f (x) = , , а вне этого интервала f (x) = 0. Найти мо-
W 9 - x2
ду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х. Какое значение вероятнее: X 1 или X 1 ?
47. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной при 0 x 5 плотностью распределения f (x) = 0,08x, а вне промежутка
48. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной функцией распределения
'0, х -2;
F (х)
0,25х + 0,5, - 2 х 2; 1, х 2.
49. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной функцией распределения
Г0, х 0;
F (х)
0,5 - 0,5cos х,
0 х п;
1, х п.
50. Найти моду, медиану, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, заданной функцией распределения
'1 - х03/ х3,
І0,
х х0 (х0 0); х х 0 .
F (х)
Контрольные вопросы
1. Что называется математическим ожиданием дискретной случайной величины?
2. Свойства математического ожидания.
3. Что называется дисперсией дискретной случайной величины?
4. Запишите свойства дисперсии.
5. Запишите формулу вычисления дисперсии.
6. Что называется средним квадратическим отклонением?
7. Доказать, что математическое ожидание числа появлений события А в одном испытании равно вероятности появленияр события А.
8. Доказать, что математическое ожидание дискретной случайной величины Х - числа появлений события А в n независимых испытаниях, в каждом из которых вероятность появления события равна р - равно произведению числа испытаний на вероятность появления события в одном испытании, т. е. доказать, что M(X) = np .
9. Доказать, что M (Y) = aM (X) + b, если Y = aX + b .
10. Доказать, что M(X - M(X)) = 0 .
11. Доказать, что M(M (X)) = M(X).
12. Доказать, что математическое ожидание дискретной случайной величины заключено между наименьшим и наибольшим её возможными значениями.
13. Доказать, что если случайные величины X1,X2,...,Xn независимы, положительны и одинаково распределены, то
X1 + X 2 + ... + X
14. Дискретная случайная величина имеет два возможных равновероятных значения x1 и x2. Доказать, что дисперсия дискретной случайной величины равна квадрату полуразности её возможных значений:
f \2
D( X)
' x2 - x1 '
15. Доказать, что если Х и Y - независимые случайные величины, то для их дисперсий справедливо равенство
D (XY) = D (X) - D(Y) + n 2 D (X) + m 2 D (Y),
где m = M (X), n = M (Y).
16. Доказать, что математическое ожидание непрерывной случайной величины заключено между её наименьшим и наибольшим значениями.
17. Случайная величина задана плотностью распределения
f (x) = 0,5е IХ . Найти математическое ожидание случайной величины.
18. Случайная величина задана плотностью распределения
f (x) = 0,5е IХ . Найти дисперсию и среднее квадратическое отклонение случайной величины.
19. Случайная величина задана плотностью распределени
0,
x a; a x b; x b.
f (x) =
b - a0,
Найти математическое ожидание случайной величины.
20. Случайная величина задана плотностью распределения
0,
x a, a x b, x b.
f (x) =
b a
0,
Найти дисперсию и среднее квадратическое отклонение случайной величины.
21. Докажите, что для одинаково распределенных взаимно независимых случайных величин математическое ожидание их среднего арифметического равно математическому ожиданию каждой из них.
22. Докажите, что для одинаково распределенных взаимно независимых случайных величин дисперсия их среднего арифметического в n раз меньше дисперсии каждой из этих величин.
23. Докажите, что для одинаково распределенных взаимно независимых случайных величин среднее квадратическое отклонение их среднего
арифметического в л[и раз меньше среднего квадратического отклонения каждой из этих величин.
24. Что называется центральным теоретическим моментом случайной величины?
Дайте примеры.
25. Что называется начальным теоретическим моментом случайной величины?
Назовите примеры.
10. Специальные законы распределения
Биномиальное распределение
По биномиальному закону распределяется дискретная случайная величина X(0; 1; 2; 3;...; m;...; n), значения которой представляют число появлений события A при n независимых испытаниях, когда P(A) = p, P(A ) = 1 - p = q. При этом вероятности pm = P(X = m) = Pn (m) вычисляются по формуле Бернулли. Такое распределение называется биномиальным, в связи с тем, что вероятности P(X = m) по форме представляют
собой члены разложения бинома
2 n-2
/~г0 0 n I /~*1 1 n1 I /~г2 2
CnP q + CnPq + CnP q
(Р + q)n
+... +
. /'im ^m n m . . r^n n „0 /^m ^m i
+ CnP q + K + CnP q = LCnP q
m = 0
Из последнего равенства следует, что сумма вероятностей значений случайной величины, распределенной по биномиальному закону, равна единице, так как
p + q = 1.
Математическое ожидание биномиального закона равно
M (X) = np .
Дисперсия для биномиального закона распределения равна
D(X) = npq,
а среднее квадратическое отклонение равно
а х=4npq.
Распределение Пуассона
По закону Пуассона распределена дискретная случайная величина X(0;1;2;3;...;m;...), вероятность значений которой P(X = m) = Pa(m) определяется формулой
m!
Pa (m)
где a - положительное число, которое называется параметром Пуассона. Формулой определяется семейство законов Пуассона, определяемое параметром a.
-a„m
e a
Значение плотности распределения Пуассона
вычисляется
m!
при помощи функции
ПУАССОЩю ;a; ЛОЖЬ).
При любом значении параметра a сумма вероятностей всех возможных значений равна единице:
го am го am
- a - a - a _a
I Pa (m) = I m e-a = e-a I ^ = e-a - ea = 1.
Математическое ожидание пуассоновского распределения равно
M (X) = a.
Дисперсия для распределения по закону Пуассона равна
D (X) = a.
К распределению Пуассона приводятся задачи простейшего потока событий.
ется при помощи функции ПУАССОН(т;а;ИСТИНА).
Потоком событий называется последовательность событий, которые наступают в случайные моменты времени. Простейшим - пуассоновским - называется поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности.
Свойство стационарности характеризуется тем, что вероятность появления m событий потока на любом промежутке времени зависит только от числа m и от длительности t промежутка времени.
Свойство отсутствия последействия характеризуется тем, что вероятность появления m событий потока на любом промежутке времени длительностью t не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка.
Свойство ординарности характеризуется тем, что вероятность появления более одного события за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события.
Интенсивностью потока называется среднее число событий, появляющихся в единицу времени.
Вероятность Pt (m) появления m событий простейшего потока интенсивностью X за время, длительностью t , определяется по формуле Пуассона
e aam
Значение функции распределения Пуассона
вычисля-
к=0
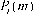
Пример. Среднее число заказов билетов, поступающих кассиру в одну минуту, равно трём. Найти вероятность того, что за 2 минуты поступит:
а) четыре заказа; б) менее четырёх заказов; в) не менее четырёх заказов.
Решение. По условию, X = 3, t = 2, к = 4.
а) Искомая вероятность того, что за 2 минуты поступит четыре вызова по формуле Пуассона
4 -6
6 - e
4!
1296 - 0,0025 24
P2(4)
0,135.
б) Событие поступило менее четырёх заказов произойдет, если наступит одно из следующих несовместных событий: 1) поступило три зака-
за; 2) поступило два заказа; 3) поступил один заказ; 4) не поступило ни одного заказа. Эти события несовместны, поэтому применима теорема сложения вероятностей несовместных событий:
P# 4) = P2 (3) + P2 (2) + P (1) + P2(0)
63 - е"б 62 - е"б 6 - е"б -6
-+-+-+ е =
3! 2! 1!
= еб(36 +18 + 6 +1) = 0,0025 - 61 = 0,1525.
в) События поступило менее четырёх заказов и поступило не менее четырёх заказов противоположны, поэтому искомая вероятность того, что за 2 минуты поступит не менее четырёх заказов,
P2(k 4) = 1 - P2(k 4) = 1 - 0,1525 = 0,8475.
Равномерное распределение
Равномерным называют распределение непрерывной случайной величины, если все значения её лежат внутри некоторого интервала и все они равновероятны.
Плотность вероятности равномерного распределения на интервале (a, b) определяется формулой
0, x a,
f(x)
1, a x b, b - a
0, x b.
Функция распределения задается формулой
0, x a,
x-a b - a ’
F(x)
a x b, x b.
Математическое ожидание равномерного закона равно
Дисперсия равномерного закона равна
D( X)
(b - a)2
12
а среднее квадратическое отклонение равно
b - a
a x = WT
Показательное распределение
Показательным - экспоненциальным - называется распределение непрерывной случайной величины, плотность распределения которой
[0 при x 0;
f^ ^ _Xx при x 0,
где X - положительное число.
Значение плотности показательного распределения Хе Xx вычис ляется с помощью функции ЭКСПРАСП(х; X; ЛОЖЬ).
При любом X выполняется необходимое условие закона распределения: интеграл в бесконечных пределах от плотности распределения равен единице:
j f (x)dx = j Хе~lxdx = - е"Xx = -(0 -1) = 1.
Функция распределения показательного закона имеет вид
Г0 при x 0,
F(Х) [l - е~Xx при x 0.
-Xx
Значение функции показательного распределения G (x) = 1 - е вычисляется с помощью функции ЭКСПРАСП( x; X; ИСТИНА).
Математическое ожидание показательного закона равно
M (X) = -Х.
X
Дисперсия показательного закона равна д X=XX
а среднее квадратическое отклонение равно
К показательному закону приводит задача о распределении вероятности случайной величины T - промежутка времени t между последовательными событиями в простейшем потоке событий. Функция распределения этой случайной величины при t 0 принимает значение, равное нулю, а при t 0
F(t) = P(T t) = P(0 T t) = Pt (m 1) = 1 - Pt (0),
где Pt (0) = e~xt.
Следовательно,
f 0 при t 0;
F (t) = \ X
[l - e Xx при t 0,
то есть промежуток времени t между последовательными событиями простейшего потока имеет показательное распределение.
Показательное распределение используется для вычисления надёжности работы элемента (простого или сложного), если последовательность отказов образует простейший поток событий с интенсивностью X. В этом случае при t 0 F(t) = P(T t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время равна
R(t) = P(T t) = 1 - F(t).
Функция R(t) = 1 - F (t) называется функцией надёжности.
При показательном распределении R(t) = 1 - (1 - e ~Xt) = e ~Xt, то есть
R(t) = e~xt.
Функция R(t), определяемая равенством, называется показательным законом надёжности.
Пример. Время безотказной работы элемента распределено по показательному закону f (t) = 0,02e ’02t (t - время в часах). Найти вероятность
безотказной работы элемента в течение 100 часов.
Решение. Интенсивность отказов X = 0,02. Вычислим вероятность безотказной работы элемента в течение 100 часов:
-0,02-100 „-2
R(100) = e
e~2 = 0,13534 * 0,14
-0,02-100
Значение показательного значения надёжности R(100) = e может быть вычислено следующим способом:
R(\00) = 1 - ЭКСПРАСП( 100; -0,02; ИСТИНА)
Нормальное распределение
Нормальным называется распределение вероятностей непрерывной
случайной величины, плотность распределения которой
( )2
(х - т)
2а
f(х)
(-да х +да),
где т, а - параметры нормального распределения, при этом а 0. Параметры нормального распределения постоянные величины. Кривая нормального распределения имеет холмообразный вид, симметричный относительно х = т . Максимальная ордината кривой, равная
т , соответствует точке х = т. По мере удаления от точки т плот-а? 2п
ность распределения убывает, и при х ^ ±да кривая распределения асимптотически приближается к оси абсцисс.
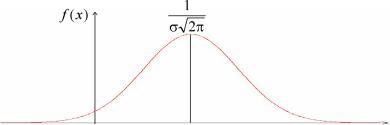
Площадь под кривой распределения равна единице.
Параметр m представляет собой математическое ожидание нормального распределения.
Параметр а - среднее квадратическое отклонение нормального распределения.
Дисперсия нормального закона равна
D( X) = о 2.
Функция нормального распределения
(х - m)2
1 х--2~
F(х) = f e 2ст dx.
Вероятность попадания нормально распределенной случайной величины на интервал (а; Ь) равна
P(a X Ь) = F(Ь) F(а).
Вероятность P(| X m | l) попадания нормально распределенной случайной величины на участок длиной 21, симметричный относительно центра рассеивания m, можно вычислить по формуле
P(| X m | l) = P(m l X m +1) = F(m +1) F(m l).
Правило трёх сигм. Вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания превысит утроенное среднее квадратическое отклонение, равна
P(| X m | 3а) = 1 0,9973 = 0,0027.
Это означает, что лишь в 0,27 % случаев может произойти отклонение, большее чем 3а. Такие события можно считать практически невозможными.
Всё это означает, что для нормально распределённой случайной величины всё рассеивание, с точностью до долей процента, укладывается на участке m ± 3а .
Таким образом, по известным математическому ожиданию и среднему квадратическому отклонению случайной величины ориентировочно можно указать интервал её практически возможных значений. Такой способ оценки интервала возможных значений называется правилом трёх сигм.
Из этого правила следует также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Этот грубый способ рекомендуется, если нет других, более точных, способов определения а.
Для нахождения значения функции нормального распределения для значения х при известных среднем и стандартном отклонении используется функция НОРМРАСП( х; среднее; стандартное отклонение; ИСТИНА).
( xm ) 2а2 х 1пЭ‘
НОРМРАСП(х; m; а; ИСТИНА)
л/2ла
В случае нахождения значения функции плотности распределения последний аргумент равен значению ЛОЖЬ.
Задачи
1. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 минут.
Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 минут.
2. Цена деления шкалы измерительного прибора равна 0,3. Показания прибора округляются до ближайшего целого деления.
Найти вероятность того, что при отсчёте будет сделана ошибка: а) меньшая 0,04; б) большая 0,05.
3. Показания электронных часов изменяются на единицу в конце каждой минуты. Найти вероятность события, состоящего в том, что в данное мгновение часы покажут время, которое отличается от истинного не более чем на 20 секунд.
4. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, равномерно распределённой в интервале (3; 9).
5. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, равномерно распределённой в интервале (35; 98).
6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х, равномерно распределённой в интервале (123; 245).
7. Математическое ожидание и среднее квадратическое отклонение нормально распределённой случайной величины X равны числам а и b, соответственно. Найти вероятность того, что в результате испытания X примет значение, заключённое в интервале (а + с; а + 2с).
| Номер задания |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| а | 32 | 20 | 12 | 42 | 25 | 52 | 13 | 28 | 65 | 78 | 22 | 26 | 35 | 62 | 15 |
| b | 64 | 5 | 4 | 16 | 3 | 7 | 2 | 4 | 5 | 11 | 64 | 5 | 4 | 16 | 3 |
| с | 2 | 5 | 3 | 1 | 2 | 3 | 2 | 4 | 5 | 3 | 2 | 7 | 4 | 3 | 5 |
| Номер задания |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| а | 56 | 30 | 12 | 42 | 25 | 52 | 33 | 48 | 65 | 78 | 22 | 26 | 25 | 62 | 15 |
| b | 4 | 3 | 10 | 16 | 3 | 9 | 2 | 8 | 5 | 11 | 64 | 5 | 4 | 16 | 3 |
| с | 3 | 2 | 3 | 1 | 2 | 5 | 2 | 3 | 5 | 7 | 2 | 6 | 4 | 3 | 5 |
10. Нормально распределённая случайная величина X задана плотностью
-(x-1)2 / 50
f(х) =
W2n
Найти математическое ожидание и дисперсию X .
11. Производится измерение диаметра бревна без систематических ошибок.
Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением а = 20 мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
12. Случайные ошибки измерения площади помещений подчинены нормальному закону со средним квадратическим отклонением а = 10 см2 и математическим ожиданием а = 0. Найти вероятность того, что из трёх независимых измерений ошибка хотя бы одного не превзойдёт по абсолютной величине 4 см2.
13. Автомат изготовляет шарики.
Шарик считается годным, если отклонение Х диаметра шарика от заданного по абсолютной величине меньше 0,5 мм. Считая, что случайная величина Х распределена нормально со средним квадратическим отклонением а = 0,3 мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.
14. Случайная величина Х распределена нормально с математическим ожиданием a = 25. Вероятность попадания Х в интервал (10; 20) равна 0,3.
Чему равна вероятность попадания Х в интервал (0; 10)?
15. Случайная величина Х распределена нормально с математическим ожиданием a = 36.
Вероятность попадания Х в интервал (55; 60) равна 0,3. Чему равна вероятность попадания Х в интервал (40; 45)?
16. Случайная величина Х распределена нормально с математическим ожиданием a = 10 и средним квадратическим отклонением а = 5. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадёт величина Х в результате испытания.
17. Случайная величина Х распределена нормально со средним квадратическим отклонением а = 4. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью 0,9973 попадёт величина Х в результате испытания.
18. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью распределения
.X 0;
, x 0.
-0,04 x
Найти вероятность того, что в результате испытания Х попадает в интервал (1; 2).
19. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью распределения
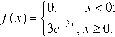
20. Непрерывная случайная величина Х распределена по показательному закону, заданному функцией распределения
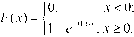
21. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение показательного закона, заданного плотностью распределения
22. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение показательного закона, заданного функцией распределения
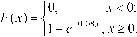
Найти математическое ожидание и среднее квадратическое отклонение случайной величины Т - времени ожидания очередной машины контролёром, - если поток машин простейший и время (в часах) между прохождениями машин через контрольный пункт распределено по показательному закону f (t) = 5e ~5t.
24. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно трём.
Найти вероятность того, что за 3 минуты поступит: а) пять вызовов; б) менее пяти вызовов; в) не менее пяти вызовов.
25. Среднее число клиентов банка в одну минуту равно двум. Найти вероятность того, что за 4 минуты придут: а) три клиента; б) менее трёх клиентов; в) не менее трех клиентов.
Поток клиентов предполагается простейшим.
26. Магазин получил 1 000 бутылок минеральной воды.
Вероятность того, что в результате перевозки одна бутылка окажется разбитой, равна 0,004. Найти вероятности того, что магазин получит разбитых бутылок: а) ровно две; б) меньше двух; в) более двух; г) хотя бы одну.
27. Устройство состоит из большого числа независимо работающих элементов с одинаковой, очень малой, вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,98.
28. Мебельная фабрика отправила на базу 1 000 изделий. Вероятность повреждения изделия в пути равна 0,001.
Найти вероятности того, что в пути будет повреждено изделий: а) ровно три; б) менее трёх; в) более трёх; г) хотя бы одно.
29. В партии из семи деталей имеется пять стандартных. Наугад отобраны четыре детали.
Составить закон распределения дискретной случайной величины Х - числа стандартных деталей среди отобранных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.