Плотность распределения

Число A равно последней цифре в номере текущего года.
1.

X	10	13	17	20	25
Р	0,4	0,3	0,1	0,15	0,05

2.

X	8	14	17	20	23
Р	0,2	0,1	0,2	0,4	0,1

3.

X	20	24	29	34	37
Р	0,2	0,3	0,25	0,15	0,1

4.

X	14	15	17	25	26
Р	0,1	0,35	0,3	0,2	0,05

5.

X	16	20	25	30	35
Р	0,2	0,15	0,15	0,3	0,2

X	0	1,5	1,9	2,5	2,9
Р	0,1	0,25	0,35	0,25	0,05

7.

X	100	114	128	144	160
Р	0,2	0,35	0,2	0,15	0,1

8.

X	45	53	67	80	95
Р	0,25	0,3	0,25	0,19	0,01

9.

X	25	45	60	75	98
Р	0,15	0,25	0,3	0,2	0,1

10.

X	60	75	80	105	110
Р	0,05	0,25	0,45	0,15	0,1

11.

X 1 2 3 7 9 10 12 Р 0,04 0,026 0,31 0,09 0,18 0,11 0,01 12 X 6 8 14 17 19 20 23 Р 0,1 0,11 0,14 0,17 0,18 0,22 0,08 13 X 20 24 28 30 34 37 40 Р 0,2 0,23 0,25 0,1 0,13 0,08 0,01 14 X 10 13 15 17 25 27 29 Р 0,1 0,12 0,23 0,3 0,17 0,05 0,03 15. X 8 16 18 20 25 30 35 Р 0,01 0,17 0,19 0,26 0,15 0,12 0,1

16.

X	0,5	1,5	1,9	2,3	2,5	2,9	3,2
Р	0,1	0,25	0,27	0,13	0,15	0,07	0,03

17.

X	100	114	125	128	144	157	160
Р	0,2	0,25	0,23	0,17	0,15	0,08	0,02

18.

X	45	53	61	67	78	80	95
Р	0,12	0,17	0,22	0,25	0,16	0,07	0,01

19.

X	25	37	45	60	68	75	98
Р	0,015	0,085	0,1	0,2	0,3	0,2	0,1

X	60	75	77	80	105	108	110
Р	0,005	0,13	0,225	0,375	0,125	0,09	0,05

21.

X	10	13	16	17	20	25	26
Р	0,1	0,3	0,3	0,1	0,13	0,05	0,02

22.

X	8	11	14	16	17	20	23
Р	0,02	0,06	0,1	0,22	0,2	0,3	0,1

23.

X	20	24	29	33	34	36	37
Р	0,1	0,17	0,25	0,16	0,12	0,1	0,1

24.

X	14	15	17	21	25	26	31
Р	0,1	0,25	0,3	0,2	0,1	0,04	0,01

25.

X	16	19	20	23	25	30	35
Р	0,08	0,12	0,15	0,3	0,15	0,11	0,09

26.

X	0	1,5	1,9	2,3	2,5	2,9	3,2
Р	0,1	0,15	0,25	0,3	0,15	0,03	0,02

27.

X	100	107	114	128	144	160
Р	0,1	0,12	0,37	0,22	0,05	0,14

28.

X	45	53	67	78	80	95
Р	0,15	0,3	0,25	0,2	0,09	0,01

29.

X	25	45	60	75	87	98
Р	0,12	0,27	0,29	0,21	0,1	0,01

30.

X	160	170	175	180	105	110
Р	0,05	0,15	0,22	0,33	0,2	0,05

31.

X	86	88	90	98	99	100
Р	0,02	0,18	0,2	0,33	0,17	0,1

X	16	17	18	19	20	21
Р	0,01	0,19	0,29	0,35	0,15	0,01

Построить графики следующих функций распределения. Определить вероятность того, что случайная величина попадёт в интервал (0,5; 0,6) для каждой из них.
31. F (x) =
33. F(x)
35. F (x) =
37. F (x)
39. F (x) =
41. F (x)
43. F(x)
0,
3 3 x +,
4 4
1,
x -1;
-1 x ; 3
1
x .
3
32. F(x)
0, x 1;
x -1, 1 x 2;
1, x 2.
x 0;
0 x 1; x1.
34. F(x)
0, x -2;
1 x
0. 5 + arcsin, - 2 x 2; 36. F(x) =
n 2
1, x 2.
0, x 0;
sin 2 x, 0 x n /4;
1, x n/4.
0, x 0;
1 - cosx, 0 x n/2;
1, x n/2.
, x 0; 1, x 0.
0, x 1;
ln x, 1 x e;
1, x e.
0, x 0;
sin x, 0 x n /2;
1, x n/2.0,
x 0;
16 _{2 Л} 5 x , 0x:
25 4
1, x 5.
4
38. F (x)
40. F (x) =
42. F (x)
44. F (x)
0, x 2;
0. 5x -1, 2 x 4;
1, x 4.0,
x 1;
1 2
(x - x), 1 x 3;
61,
x 3.
x 0.
0, x 0;
x2/e2, 0 x e;
1, x e.
45. F (x)0,
x3 - x
60
x 1;
1 x 4; x 4.
46. F(x)
0,
x4 - 81 175 :
x 3;
3 x 4; x 4.
0, x 0;
47. F(x)
49. F (x)
64 _{2 л} 7 x2,0 x ;
49 8
48. F(x)
0,
x3 + 8 16 '1,
0, x 0;
1 - e-2 x, x 0.
50. F(x)
x -2;
- 2 x 2; x 2.
0, x 0;
1 - e "x, x 0.

Контрольные вопросы

1. Что называется функцией распределения случайной величины?
2. Какая случайная величина называется непрерывной?
3. Какими свойствами обладает функция распределения случайной величины?
4. Какой функцией является функция распределения дискретной случайной величины?
5. Чем характеризуется функция распределения непрерывной случайной величины?
6. Докажите монотонность изменения функции распределения.
7. Как найти функцию распределения дискретной случайной величины по заданному закону её распределения?
8. Как составить закон распределения дискретной случайной величины по её функции распределения?
9. Чему равна вероятность принятия конкретного значения для непрерывной случайной величины?
10. В каком промежутке лежат значения функции распределения?
11. Какие предельные соотношения справедливы для функции распределения?
12. Как найти вероятность того, что случайная величина примет значения из некоторого интервала?
13. Чем отличаются термины функция распределения и интегральная функция распределения?
14. Чем характеризуется линия, изображающая график функции распределения дискретной случайной величины?
15. Чем характеризуется линия, изображающая график непрерывной случайной величины?
16. Чему равно минимальное значение функции распределения?
17. В каких пределах изменяется функция распределения?
18. Чему равно максимальное значение функции распределения?
19. Определить вероятность того, что случайная величина примет значение из интервала ( 1; 0,5), если ее интегральная функция распределения равна
0, х -1;
F(х) =
0. 4, -1 х 0,6;
1, х 0,6.
20. Определить вероятность того, что случайная величина примет значение из интервала (-0,2; 0,6), если ее интегральная функция распределения равна
0, х 0;
F (х)
* 0,5, 0 х 0,6;
1, х 0,6.

Плотность распределения

Производная от функции распределения F (х)
f ( х) = F X x),
называется плотностью распределения f (х) случайной величины X.
Плотность распределения существует только для непрерывных случайных величин. Для описания распределения дискретной случайной величины плотность распределения вероятности неприменима.
График плотности распределения называют кривой распределения.
Свойства плотности распределения

1. Плотность распределения неотрицательна:
f (х) ^ 0.
Это следует из того, что F (х) - неубывающая функция.
2. Вероятность попадания значения случайной величины X в интервал [a, b] равна
b
P(a x b) = J f (x)dx.
3. Функция распределения F (x) выражается через плотность f (x) по формуле
X
F (x) = J f (x)dx.
да
4. Несобственный интеграл от плотности распределения в бесконечных пределах равен единице:
да
J f (x)dx = 1.
да
Если все возможные значения случайной величины находятся на отрезке [a, b], то, очевидно,
b
J f (x)dx = 1.

Задачи

Найти плотность распределения случайной величины по заданной функции распределения
1. F (x)
0,
64 ₂ і x 2

x 0;
7
0 x ;
8
7
x .
8
2. F(x)=
0,
x ^ + 8 16 ;
x 2;
2 x 2; x 2.0,
x 1;
3. F(x)
3 3 1
x + , 1 x ;
4 4 3
1, x 1.
3
4. F(x)
'0,
x 1,
1,
x 1;
1 x 2; x 2.
5. F(x) =
'0, x 0;
x2, 0 x 1;
1, x 1.
6. F (x)
0,
sin x, 1,
x 0;
0 x n/2; x n/2.
7. F(x)= 1, x 2.
0, x 0,
1 - cosx,0 x n/2,
1, x n/2.
9. F (x) =
'0, x 0;
sin 2 x, 0 x n /4; 1, x n/4.
10. F(x)
0, x 2;
0. 5x -1, 2 x 4;
1, x 4.
11. F (x)
13. F (x)
15. F(x)
17. F(x)
19. F(x)
0,
16
251,
x 0;
5
0 x ; 4 5
x .
4
12. F(x)
0,
1 - .2
x 1;
x), 1 x 3;
x 3.
, x 0; 1, x 0.
14. F ( x )
x 0; x 0.
'0, x 1;
ln x, 1 x e; 1, x e.
|0, x 0;
[1 - e "2 x, x 0.
16. F ( x )
18. F(x)
0,
x 2 / e 2,
1,fІ1 - e-x,
x 0;
0 x e; x e.
x 0; x 0.
0,
x3 - x
60 :
x 1;
1 x 4; x 4.
20. F(x)0,
81
175
x 3;
3 x 4; x 4.
задана на всей оси ОХ равенством f (x) = метр С.
2C 1 + x'
. Найти постоянный пара-
В следующих заданиях задана плотность распределения f (x) непрерывной случайной величины Х. Найти функцию распределения F (х).
0, х 0; cosх, 0 х п/2; 0, х п/2.
0, х 0;
sin х, 0 х п /2; 0, х п/2.
22. f (х) =
23. f(х)=
0, х п/6;
3sin3x, п/6 х п/3; 0, х п/3.
0, х 1;
х - 0,5, 1 х 2; 0, х 2.
24. f (х) =
25. f (х) =
0,
3х2 - 2х
х 1;0,
х 0;
32
х, 0 х 1,25; 25
0, х 1,25.
27. f(х)=
26. f (х) =
1 х 4; х 4.
480,
0, х 1;
1
, 1 х е; х
0, х е.0,
х 0;
28. f (х) =
29. f (х) =
0,25х3, 0 х 2;0,
х 2.
0, 3х2
х -2;
х 1;
1 х 6; х 6.
0,
2 х - 2
30. f (х) =
31. Дх) =
- 2 х 2;
16
0, х 2.
250,
32. Плотность распределения непрерывной случайной величины Х
задана на всей оси ОХ равенством f (х) = раметр С.
Найти постоянный па-
4C
ех + е ~х
33. Плотность распределения непрерывной случайной величины Х задана на интервале (0;п/2) равенством f (x) = C sin 2x, вне этого интервала f (x) = 0. Найти постоянный параметр С.
34. Плотность распределения непрерывной случайной величины Х задана на интервале (0;1) равенством f (x) = C arctg x, вне этого интервала f (x) = 0. Найти постоянный параметр С.
35. Плотность распределения непрерывной случайной величины Х
задана на интервале (1;2) равенством f (x)
1
C1, вне этого интервала f (x) = 0. Найти постоянный параметр С.
равенством f (x) = 2, вне этого интер
36. Плотность распределения непрерывной случайной величины Х '3 - C 3 + C
задана на промежутке вала f (x) = 0. Найти постоянный параметр С.
37. Плотность распределения непрерывной случайной величины Х задана на промежутке (5;8] равенством f (x) = C, вне этого интервала
f (x) = 0. Найти постоянный параметр С.
38. Плотность распределения непрерывной случайной величины Х задана на промежутке (C;4] равенством f (x) = 5, вне этого интервала
f (x) = 0. Найти постоянный параметр С.
39. Плотность распределения непрерывной случайной величины Х задана на промежутке (C;15] равенством f (x) = 3, вне этого интервала
f (x) = 0. Найти постоянный параметр С.
40. Плотность распределения непрерывной случайной величины Х задана на промежутке (1;10] равенством f (x) = 2C, вне этого интервала
f (x) = 0. Найти постоянный параметр С.

Контрольные вопросы

1. Что называют плотностью распределения вероятностей непрерывной случайной величины?
2. Как найти вероятность того, что непрерывная случайная величина принимает значение, принадлежащее интервалу (a, b) ?
3. Какими свойствами обладает плотность распределения?
4. Как найти плотность распределения по функции распределения?
5. Как найти функцию распределения по плотности распределения?
6. Какова область изменения плотности распределения?
7. Какой может быть область изменения функции плотности распределения?
8. Что такое плотность вероятностей?
9. Как определить дифференциальную функцию распределения?
10. Чему равен несобственный интеграл от плотности распределения в пределах от -да до да?
11. На основе какого свойства плотности распределения можно находить значения её параметра?
12. Как вычислить вероятность попадания случайной величины в интервал (a, b), используя функцию распределения?
13. Как вычислить вероятность попадания случайной величины в интервал (a, b), используя функцию плотности распределения?
14. Для каких случайных величин вводится понятие плотности распределения?
15. Можно ли по виду функции плотности распределения судить о значениях, принимаемых случайной величиной?
16. Возможно ли построить функцию плотности распределения для дискретной случайной величины?
17. Объясните вероятностный смысл плотности распределения.
18. Запишите плотность вероятности для равномерного закона распределения случайной величины.

Числовые характеристики случайной величины

Любая форма закона распределения случайной величины, например, самая универсальная - функция распределения, полностью определяет случайную величину с вероятностной точки зрения. Существуют более простые, хотя и менее исчерпывающие, характеристики случайной величины, в определенной мере характеризующие её существенные черты, например, среднее значение или степень разбросанности значений относительно среднего.

Такие характеристики, назначение которых - выразить числом наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.
В теории вероятностей основными числовыми характеристиками случайной величины являются её математическое ожидание и дисперсия.
Математическим ожиданием случайной величины называется число, которое обозначается m_x или M(X) и вычисляется по формулам:
- для дискретной случайной величины X = (x₁; x₂; к; x_n )
n
mx = Z xiPi , i=1
где Pi = P( X = x );
- для непрерывной случайной величины X с плотностью распределения f ( x)
+
m_x = J xf (x)dx.
Математическое ожидание определяет значение случайной величины, около которого группируются все её возможные значения, и имеет определенную связь со средним арифметическим наблюдаемых значений при большом числе опытов. Эта связь того же рода, что и связь между относительной частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюдаемых значений случайной величины приближается (сходится по вероятности) к её математическому ожиданию.
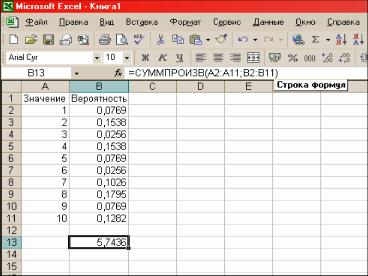
Рассмотрим пример нахождения математического ожидания для ряда дискретных значений.
На рисунке 1 представлен ряд дискретных значений, причём в левом столбце представлены значения, а в правом - их вероятности.
Для нахождения математического ожидания представленного ряда значений дискретной случайной величины X вводим формулу:

=СУММПРОИЗВ(Л2:Л11;Б2:Б11).

Результат вычислений математического ожидания помещён в ячейку
В13.

Математическое ожидание числа появления события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равно произведению числа испытаний на вероятность появления события в одном испытании:
M (X) = np.
Дисперсией случайной величины называется число, которое обозначается а2 или D( X) и вычисляется по формулам:
- для дискретной случайной величины
а 2 = Х(xi mx)2 - Pi;
i=1
- для непрерывной случайной величины
а2 = J (x - mx )2 - f(x)dx -
x
Вычисление дисперсии можно производить по формуле
D( X) = M (X2) m2,
где M (X2) - математическое ожидание квадрата случайной величины.
Для дискретной случайной величины
M(X2) = ?x2 - Pi ; i=1
для непрерывной случайной величины
M(X2) = J x2 - f (x)dx -
x
Дисперсия имеет размерность квадрата случайной величины.
Дисперсия позволяет оценить рассеяние возможных значений случайной величины вокруг её среднего значения. Дисперсия случайной величины есть неслучайная (постоянная) величина.
Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
D( X) = npq.
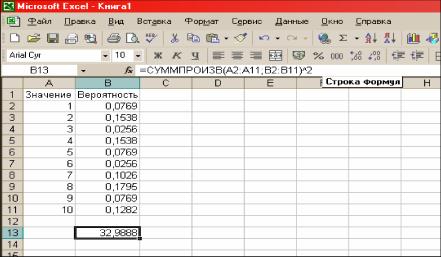
Рассмотрим пример нахождения дисперсии случайной величины. Для нахождения дисперсии воспользуемся формулой
D( X) = M (X 2) [ M (X )]2.
Найдём математическое ожидание и возведём его в квадрат (рис. 2). Результат вычислений представлен в ячейке B13:


Теперь найдём M(X2). Для этого значения случайной величины возведём в квадрат и запишем эти значения в столбец C. Затем найдём математическое ожидание для случайной величины X2.

Результат вычислений представлен в ячейке C13 (рис. 3):

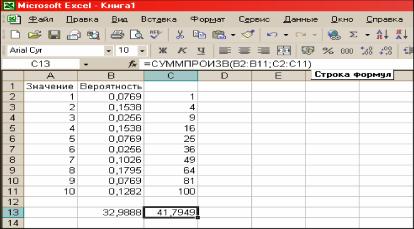
После этого, согласно формуле D( X) = M (X 2) - [M (X )]2, достаточно вычислить разность между значениями ячеек C13 и B13. В нашем случае дисперсия равна 8,8061.
Свойства математического ожидания и дисперсии
1. Математическое ожидание постоянной величины равно самой этой постоянной:
M(C) = C.
2. Постоянную величину можно выносить за знак математического ожидания:
M (CX ) = CM ( X ).
3. Математическое ожидание от суммы или разности случайных величин равно сумме или разности их математических ожиданий:
M (X + Y) = M (X) + M (Y);
M(X - Y) = M(X) - M(Y).
4. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
M (XY) = M (X )M (Y);
5. Дисперсия постоянной величины равна нулю:
D(C) = 0.
6. Постоянную величину можно выносить за знак дисперсии, возведя её в квадрат:
D(CX) = C 2 D( X).
7. Дисперсия от суммы или разности случайных величин равна сумме их дисперсий:
D(X ± Y) = D(X) + D(Y).
В теории вероятностей используют характеристику разброса значений случайной величины относительно её среднего значения
а х=v d( x )=
которая называется средним квадратическим отклонением и имеет размерность случайной величины.
Дисперсия имеет размерность, равную квадрату размерности случайной величины, а математическое ожидание и среднее квадратическое отклонение - ту же размерность, что и случайная величина.
Модой M₀(X) дискретной случайной величины X называют её наиболее вероятное значение.
Модой M₀(X) непрерывной случайной величины X называют то её возможное значение, которому соответствует локальный максимум плотности распределения.
Медианой M_e (X) случайной величины X называют то её возможное значение, которое определяется равенством
P[X Me (X)] = P[X Me (X)] .
Медиана обычно не определяется для дискретной случайной величины. Геометрически медиану для непрерывно распределенной случайной величины можно истолковать как точку, в которой ордината f (х) делит площадь, ограниченную кривой распределения, пополам.

Задачи

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной одним из следующих законов распределения:

Х	10	13	17	20	25
Р	0,4	0,3	0,1	0,15	0,05

2.

Х	8	14	17	20	23
Р	0,2	0,1	0,2	0,4	0,1

3.

Х	20	24	29	34	37
Р	0,2	0,3	0,25	0,15	0,1

4.

Х	14	15	17	25	26
Р	0,1	0,35	0,3	0,2	0,05

5.

Х	16	20	25	30	35
Р	0,2	0,15	0,15	0,3	0,2

Х	0	1,5	1,9	2,5	2,9
Р	0,1	0,25	0,35	0,25	0,05

7.

X	100	114	128	144	160
Р	0,2	0,35	0,2	0,15	0,1

8.

X	45	53	67	80	95
Р	0,25	0,3	0,25	0,19	0,01

9.

X	25	45	60	75	98
Р	0,15	0,25	0,3	0,2	0,1

10.

X	60	75	80	105	110
Р	0,05	0,25	0,45	0,15	0,1

11.

X	1	2	3	7	9	10	12
Р	0,04	0,26	0,31	0,09	0,18	0,11	0,01

12.

X	6	8	14	17	19	20	23
Р	0,1	0,11	0,14	0,17	0,18	0,22	0,08

13.

X	20	24	28	30	34	37	40
Р	0,1	0,23	0,25	0,18	0,13	0,08	0,03

14.

X	10	13	15	17	25	27	29
Р	0,1	0,12	0,23	0,3	0,17	0,05	0,03

15.

X	8	16	18	20	25	30	35
Р	0,01	0,17	0,19	0,26	0,15	0,12	0,1

16.

X	0,5	1,5	1,9	2,3	2,5	2,9	3,2
Р	0,1	0,25	0,27	0,13	0,15	0,07	0,03

17.

X	100	114	125	128	144	157	160
Р	0,1	0,25	0,23	0,17	0,15	0,08	0,02

18.

X	45	53	61	67	78	80	95
Р	0,12	0,17	0,22	0,25	0,16	0,07	0,01

19.

X	25	37	45	60	68	75	98
Р	0,015	0,085	0,125	0,17	0,3	0,2	0,1

X	60	75	77	80	105	108	110
Р	0,005	0,13	0,225	0,375	0,125	0,09	0,05

21.

X	10	13	16	17	20	25	26
Р	0,1	0,3	0,3	0,1	0,13	0,05	0,02

22.

X	8	11	14	16	17	20	23
Р	0,02	0,06	0,1	0,22	0,2	0,3	0,1

23.

X	20	24	29	33	34	36	37
Р	0,1	0,17	0,25	0,16	0,12	0,1	0,1

24.

X	14	15	17	21	25	26	31
Р	0,1	0,25	0,3	0,2	0,1	0,04	0,01

25.

X	16	19	20	23	25	30	35
Р	0,08	0,12	0,15	0,3	0,15	0,11	0,09

26.

X	0	1,5	1,9	2,3	2,5	2,9	3,2
Р	0,1	0,15	0,25	0,3	0,15	0,03	0,02

27.

X	100	107	114	128	144	160
Р	0,1	0,12	0,37	0,22	0,05	0,14

28.

X	45	53	67	78	80	95
Р	0,15	0,3	0,25	0,2	0,09	0,01

29.

X	25	45	60	75	87	98
Р	0,12	0,27	0,29	0,21	0,1	0,01

30.

X	160	170	175	180	105	110
Р	0,05	0,15	0,2	0,35	0,15	0,1

31. Дискретная случайная величина принимает три возможных значения: x₁ = 5 с вероятностью p₁ = 0,5 ; x₂ = 8 с вероятностью р₂ = 0,3; х₃ с вероятностью р₃. Найти значения величин х₃ и р₃, зная, что математическое ожидание случайной величины M (X) = 7.
32. Возможные значения дискретной случайной величины x₁ = -1; х₂ = 0; х₃ = 1, а математические ожидания этой величины и её квадрата равны соответственно: M (X) = 0,1; M (X2) = 0,9.

Найти закон распределения этой случайной величины и её функцию распределения.
33. Для каждого из вариантов задания найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 4X + 5Y, если известны математические ожидания M(X) и M(Y) и дисперсии D(X) и D(Y) случайных величин X и Y:

Номер зада ния	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M (X)	15	3,4	103	19	25	11	46	39	93	74	45	14	12	20	54
M (Y)	61	4,6	321	31	54	90	68	32	22	27	41	17	8	31	50
D( X)	0,02	7,1	32	2,4	6,8	0,2	8	3	4,1	0,8	5	4	2	0,3	5,8
D(Y)	0,04	1,2	46	1,1	7,7	0,4	2	4	3,3	0,1	3	8	6	0,1	8,7

34. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 3X - 2Y, если известны математические ожидания и дисперсии случайных величин X и Y :

Номер зада ния	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M (X)	32	25	112	34	55	46	73	54	123	236	46	24	53	167	41
M (Y)	16	127	57	13	67	37	112	33	101	213	78	93	45	321	57
D( X)	4	12	42	23	3	2	11	14	13	17	5	11	3	34	3
D(Y)	6	19	12	40	4	6	21	15	17	6	8	9	6	67	5

35. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 7X + 4Y, если известны математические ожидания и дисперсии случайных величин X и Y:

Номер зада ния	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M (X)	3,5	2,3	4,8	9,4	5,5	5	3,9	8,5	4,3	6,5	2,1	5,4	7,1	8,7	3
M (Y)	2,7	2,1	8,6	2,3	7,7	7	1,1	2,8	9,5	2,7	2,9	4,7	2,7	3,3	2
D( X)	0,1	0,4	0,2	1,1	0,3	1	2,1	1,4	1,3	0,4	0,1	0,6	0,3	0,6	1
D(Y)	0,5	0,3	0,9	1,9	0,2	5	3,5	0,5	1,8	0,6	0,5	0,5	1,5	1,3	5

36. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 6X - 3Y, если известны математические ожидания и дисперсии случайных величин X и Y :

Номер зада ния	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M (X)	23	51	12	37	54	416	43	59	196	316	61	14	73	163	98
M (Y)	56	207	57	18	69	317	135	38	185	231	75	9	45	311	37
D( X)	3	21	42	29	7	4	27	31	28	25	6	11	3	34	8
D(Y)	7	17	12	42	2	3	33	56	57	63	3	5	7	55	4

37. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z = 8X - 5Y + 4, если известны математические ожидания и дисперсии случайных величин X и Y :

Номер зада ния	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
M (X)	54	31	12	82	54	168	43	59	106	116	81	14	33	113	68
M (Y)	87	17	57	18	69	217	135	38	185	231	55	79	45	311	47
D( X)	2	5	22	15	7	4	27	31	28	25	6	10	4	84	11
D(Y)	8	7	11	5	2	3	33	56	57	63	3	5	6	95	19

38.

Содержание раздела

---