Устойчивость степени нечеткости ПОСП

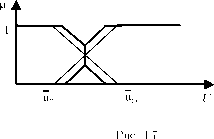
Интерпретация. Рассмотрим процесс описания человеком реальных объектов. Мы не имеем никакой неопределенности при лингвистическом описании объекта, имеющего ’’физическое" значение признака u (Рис.

4.3). Мы присвоим ему лингвистическое значение ai без сомнений и колебаний.
Мы можем повторить данные рассуждения для объекта, имеющего ’’физическое" значение признака us. Мы без колебаний выбираем термин а₂ для его лингвистического описания без сомнений. Мы начинаем испытывать трудности при выборе

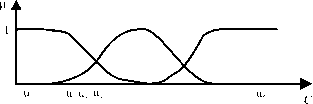
Рис. 4.3:

лингвистического значения для объекта, имеющего ’’физическое" значение признака и₂. Эти трудности возрастают (из) и достигают максимального значения при описании объектов, имеющих ’’физическое" значение признака и₄: для таких объектов оба лингвистических значения одинаково подходят.
Если мы рассмотрим значения подынтегральной функции
V(st, и) = 1 - (iq (и) - /ц* (и)) в этих точках, мы можем увидеть, что 0 = ) = у^,щ) n(st, и2) n(st, из) n(st, и4) = 1.
Таким образом, значение интеграла ( 4.6) мы действительно можем интерпретировать как среднюю степень трудностей описания человеком реальных объектов (ситуаций) в рамках соответствующего ПОСП.
Рассмотрим некоторые свойства функционала ( 4.6). Для этого рассмотрим следующие подмножества L:
L - множество кусочно - линейных функций из L, которые являются линейными на множестве неопределенности U = {и Е U : Vj (1 j t) 0 /ij(и) 1},
L - множество функций из L, являющихся кусочно-линейными на U (включая
U).
Теорема 5 Пусть s_t Е G_t(L). Тогда Дs_t) = 2Щ^^е d = \U|-
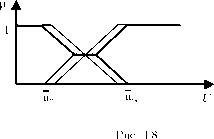
Доказательство. Рассмотрим простейший случай t = 2 (Рис.

4.4).
Зафиксируем две точки:
й₂ь - левая ненулевая граница i_a2 (и) и
U\r - правая ненулевая граница ц_аі (и).
Значение интеграла ( 4.6) не равно нулю только на отрезке \n_2L, n\_R]. Таким образом,
= щ ]_?(1 (u) Vq (u)))du =
(4.7)
= Щ\!_ (1 - ?(u) - (u)))du-
Используя простейшие формулы элементарной геометрии, мы можем написать:

v1 (u) 1	| 1 d (u1R u), { 0	если u u2L если u2L u u1R , если u u1R	(4.8)
V2 (u) j	\ 0 1 (u u2L), 1,	если u u2L если u2L u u1R , если u u1R	(4.9)

где d = u_1R u_2L.
Подставляя ( 4.8), ( 4.9) в ( 4.6) и вспоминая ( 4.5), мы можем написать:
= U fiL(1 (ViI(u) Vq (u)))du =
Ul1R+U2L) (1 (ViI(u) Vq (u)))du+ + i;U_R+~_U2L)(1 (Vi1(u) Vq(u)))du * (um + u_2L 2u)du
U
UlR


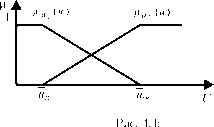
Доказательство теоремы достаточно очевидно.
Так как любая s_t Е G_t(L) может быть со сколь угодно большой точностью аппроксимирована совокупностью нечетких множеств из s_t Е G_t(L), то соотношение ( 4.10) справедливо для всех s_t Е G_t(L).
Пусть g некоторая взаимно-однозначная функция, определенная на U. Эта функция индуцирует преобразование некоторой s_t Е G_t(L), определенной на универсальном множестве U в g(s_t), определенной на универсальном множестве U', где
U' = g(U) = {и' : и' = g(u), и Е U}.
Это преобразование можно определить следующим образом: g(s_t) есть множество функций принадлежности {у1(и'),y'_t(u')}, где
у,j(и') = vj(g(u)) = ?з(g-1 (и')) = ?з(и),?з(и) Е st, j t.
Следующий пример иллюстрирует данное определение.
Пример 20 Пусть s_t Е G_t(L), U - универсум s_t и g - растяжение (сжатие) универсума U. В этом случае g(s_t) есть совокупность функций принадлежности, полученная из s_t таким, же растяжением, (сжатием).
Теорема 7 Пусть s_t Е G_t(L), U - универсум s_t, g - некоторая, линейная взаимнооднозначная функция на, U и ?(s_t) = 0. Тогда ?(s_t) = ?(g(s_t)).
Доказательство. Рассмотрим простейший случай t = 2 (смотри доказательство теоремы 5). Если s₂ Е G₂(L), то, в силу ортогональности,
уаі (и') 1 уа2 (и') ^и Е U
Таким образом,
= U J2rR (1 - (и) - Уі* (u)))du =
JUa (2)(1 - (?аі (и) - ?а₂ (и)))ди+ + ?1R( 1 ₎(1 - (?а₂ (и) - Уаі (u)))du
(4,11)
It? (2)(1 - ((1 - ?а₂ (и)) - ?а₂ (u)))du+
2
IUI
U2L
U1R
+ f?R( 1 )(1 - ((1 - ?аі (и)) - ?аі (u)))du
_2_ IUI
('} ?а2 (u)du + QR 1) ?аі (u)du
Повторяя данные рассуждения для s'_t = g(s_t), мы можем написать:
2
Г9(Ча)( 2)) ря(иш) ? (s2)
у' (u')du'
у! (и')ди' +
\g(U )|
g( (2))
С(2?)
Производя замену переменных u' = g(u), мы можем переписать ( 4.12) следующим образом:
9(а]_ ( 2 ))
mL (g(u))dg{u)+
? (4)
C9(9
Jaiw
g(u2L)
\g(u )|
g(uiR)
9(9-I( 1 ))r ai
mL (g(u))dg(u)
(4,13)
9ai ( 2 )
U2L
ju
JU‘
M_a2 (u)g' (u)du+
+ C-Ri₎ Mai (u)g'(u)du
\,(U )\
Последнее соотношение в ( 4.13) является следствием определения g(s_t). Равенство ?(s₂) = ?(g(s₂)) эквивалентно равенству
JRa {~2) Ma2 (u)du + 1) Маг (u)du
/URL (} Ma2 (u)g'(u)du + QR( 1
2
\и \
(4,14)
UiR 9ai ( 2 )
M_ai (u)g'(u)du
\g(u )\
Равенство ( 4.14) мы можем переписать как


Г9-1 ( 2 ) ¦JU 2L
j du+
Mai (u)
_1 _ яПЩ \U\ _\g(u )\
I Г U1R
+ J 9-1 (1)
Ма2 (u)
(4.15)
сел d_u = о
\g(U)\) au 0
1
\U \
Если g(u) - линейная функция, то g(u) = ku + а, гДе k, а некоторые константы. Значение g'(u) = k = 9(uUlUUI' ^u₂, u₁ E U, и, в частности, g'(u) = Используя
последнее равенство, мы можем написать:
_ g'(u) = ₀ \U\ \g(U)\ -
Таким образом, ( 4.15) справедливо.
Для доказательства теоремы в общем случае t 2 мы должны повторить наши рассуждения для всех областей неопределенности \uj^ uj_-1yR] (2 j t).
Теорема доказана.
Это свойство означает, что человек описывает разнотипные объекты в рамках некоторого семантического пространства с равными трудностями, если физические параметры объектов одного типа можно получить из параметров объектов другого типа некоторым линейным преобразованием. Например, используя множество термов (высокий, средний, низкий} мы описываем людей, деревья, здания с одинаковыми трудностями; используя множество значений (очень близко, близко, не близко, далеко} мы описываем расстояния между молекулами, улицами в городе, городами на карте и т.п. с одинаковыми трудностями.
Степень нечеткости одного множества, индуцированная ?(s_t) может быть определена как степень нечеткости тривиальной совокупности нечетких множеств, определенной одним множеством m(u)‘
He трудно доказать, что ( 4.16) обладает всеми свойствами степени нечеткости множества, изложенными в 1.5.4.

Методика выбора оптимального множества значений качественного признака

Вернемся к примеру 19 и проблеме 1. На основе свойств степени нечеткости ПОСП (раздел 4.4) и ее интерпретации (с. 60), мы можем сформулировать следующую методику выбора оптимально множества значений качественных признаков.
1. Формируются все возможные (все ’’разумные") множества значений признака.
2. Каждое множество значений признака представляется в виде полного ортогонального семантического пространства.
3. Для каждого множества значений вычисляется степень нечеткости ПОСП.
4. В качестве оптимального множества значений как по критерию 1, так и по критерию 2, выбирается то множество степень нечеткости которого минимальна.

Устойчивость степени нечеткости ПОСП

Одним из ограничений методики выбора оптимального множества значений качественных признаков (раздел 4.4), существенно используемых при ее анализе, является предположение об одинаковости функций принадлежности используемых лингвистических понятий. Интуитивно ясно, что функции принадлежности у всех людей не могут быть полностью одинаковыми.

Данный тезис можно проиллюстрировать следующими примерами.
Если попросить оценить возраст юношу и пожилого человека, то, скорее всего, их оценки будут различаться: для молодого человека 50 лет - это старость, для пожилого - зрелый возраст. То же самое может наблюдаться при оценке роста низким и высоким человеком: функции принадлежности соответствующих лингвистических понятий у первого будут сдвинуты влево, у второго - вправо относительно друг друга.

Подобные ситуации давно были замечены и даже послужили основой сюжета ряда детективов.
Более сложное взаимодействие между семантикой одинаковых терминов может наблюдаться у людей разных национальностей (проживающих в различных геокли-матических зонах) в силу принципа лингвистической дополнительности - одного из принципов психолингвистики [8]. Так, например, жители крайнего севера (эскимосы, чукчи) различают несколько оттенков снега, соответствующих его состоянию, финны имеют несколько названий для синего цвета.
Для отражения перечисленных факторов будем считать, что функции принадлежностей источника информации и пользователя не совпадают, а могут находиться в некоторой полосе ширины 6, то есть заданы с некоторой ’’точностью" 6 (рис. 4.5).
Выразим основные параметры ($і и 8₂), необходимые для анализа модели, как функции от 8. Для этого воспользуемся элементарными соотношениями из тригонометрии.
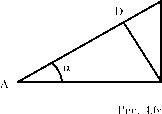
Обозначим через а угол наклона p_a2 (u) в точке U_2L (рис. 4.5).

Тогда tan а = Ц, где d = U₁r u_2L- Рассмотрим более подробно треугольник ABC, где ABAC = а, \BC\ = f, \CD\ = 2 \AC\ = у (рис. 4.6).

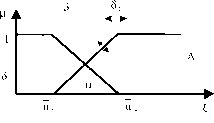
Рис. 4.5:

\вс\ Из AABC следует, что tan а Таким образом, = у и, следовательно,
8₁ = 8₂ d. (4.17)
Выразим 8₂ через 8 и d. С помощью простейших тригонометрических соотношений из ACDB и AADC, получаем, что 82(1 + d2) = 8^d2.
Из последнего равенства получаем:
82 = dp (1 + d2)
или
82 = d V1 + d2. (4.18)
Вспоминая соотношение 8₁ = 8₂d, получаем:
8₁ = 8Vl + d2. (4.19)
Имея выражения для 8₂ и 8₁ (( 4.18) и ( 4.19) соответственно) можно оценить средние индивидуальные потери информации и шумы для описанной модели (будем называть ее 8 - модель и обозначать G6_t (L)), а также степень нечеткости соответствующего ПОСП.

Степень нечеткости в 8 - модели

Построим обобщение формулы ( 4.6) для случая 8 модели. Для этого рассмотрим некоторую точку u Е U (рис.

4.5). Достаточно очевидно, что что нижние и верхние оценки для степени нечеткости в точке ?(s_t) и Дs_t) будут достигаться при функциях принадлежности, имеющих изображенный на рис.

4.7 и 4.8 вид соответственно (на рис. 4.7 изображена наиболее близкая к характеристической функция принадлежности; на рис.

4.8 - наиболее близкая к функции ц(и) = 0.5Vu Е U функция принадлежности из данной области).
Для формализации записи таких функций введем следующие величины:
q = {R, L}, (4.20)

(4,21)
\ R, если q = L, \ L, если q = R,
UjL + Uj-1,R $1 UjL + Uj-1,R $1
(4.22)
Тогда
V(st,u) = 1 - (Д (u) - i| (u)) ,
(4.23)
гд?
(4.24)(u) = maxijt {if(u),iR(u)}
R, yR(u) yR(u) q ’ L, yR(u) iR(u)
(u) = maxijt_j=_i*1 (u)) = f 1 - (i|(u) - iq(u)) , u € U\U I 0.5, u G U
V(st,u)
(4.25)
Аналогично ( 4.6) нижние и верхние оценки -(s_t) имеют следующий вид:
(4.26)
(4.27)
-(st) = Щ J n(st,u)du’
-(st) = щ J_v n(st,u)du.
Теорема 8 Пусть s₂ € GS₂(L) Тогда
d (1 - $2)2 21U |
d (1 + 2$2) 2|U |
- (s2)
(s2) При выводе ( 4.28) использовалась замена переменных z = u u_2L и соотношение Si = dS2 ( 4.17).
Аналогично вычислению ?(s₂), представим й(s₂) следующим образом:
I 51 fU 1R + -f
тТ I n(S2,u)du =-1 I V(s2, u)du
\U \ JU \U \ Ju_2L-51
'U2L+U1R
2
y(s₂,u)du
\U I Ju 2L-Д
U2L~ 2
u2L+ulR ^1
2 2
(- 5i
I ulR
-- u
2
Si
2
du +
, u2L+u1 R
2
+Ш I- - du \ U \ J u2L+u1 R ?l
2 (u u_2L) du
ddu +
d\U \
f 5i
U2L -2
f 5i
U2L 2
A Si =
+ U ~2~
(d S_l) du
I 51
U2L 2
d ^1
d /*2 ~21 d
d- + 2 zdz (d Si) -
2 51 2
. .
2(d d si) + 2 _M +
+ A
\U \
iL = \U \
d\U \ 2
d\U \
d Si d dS2 d . .
2\U\ + \U\ = 2\U\ + \U\ = 2\U\ (+ 2)
(4.29)
При выводе ( 4.29) использовалась замена переменных и соотношение S_l = dS₂
( 4.17).
Теорема доказана.
Терема 8 довольно легко обобщается на случай более двух значений признака. Теорема 9 Пусть s_t Е Gf (L).
c(st)
D (1 S2)2
2\U\ ¦
C(st) =
D (1 + 2S2) 2\U\ :
где D Xj=i dj,j+i dj,j+i ujR uj+i,L-
Доказательство аналогично доказательству теоремы 5 с учетом теоремы 8.
Сравнивая утверждения теорем 5 и 9 мы можем утверждать, что малые значения 8 не оказывают существенного влияния на значение степени нечеткости ПОСП, то есть степень нечеткость является устойчивой.
Это позволяет утверждать, что сформулированная нами методика выбора оптимального множества значений качественных признаков (раздел 4.4) может применяться в практических задачах. На основе теоремы 7 можно утверждать, что мы можем строить оптимальные множества значений качественных признаков в наиболее простых, ясных для эксперта ситуациях, а использовать их во всех случаях, получающихся из данного некоторым линейным преобразованием универсального множества.
В заключение отметим, что изложенные в данной главе результаты могут рассматриваться как первые наброски общей теории измерения степени нечеткости нечетких объектов. Эти исследования имеют не только теоретический интерес, но и позволяют решать практические задачи.

Так, например, можно показать, что степень нечеткости связана с показателями качества поиска информации в нечетких (лингвистических) базах данных [44], [41]. Это означает, что мы имеем возможность на основе качества исходной информации ’’вычислить" предельно возможные показатели качества поиска информации в таких базах данных.

Представляет интерес определение понятия степени нечеткости для других нечетких объектов. Определение степени нечеткости нечеткого отношения позволит, например, определять степень нечеткости систем логического вывода, изучить зависимость качества исходной информации и нечеткости вывода с одной стороны и качества работы экспертных систем, нечетких контроллеров и других прикладных нечетких систем с другой.

Литература

[1] Авдюнина Л.И., Черезова Н.Н. Лингвистический подход к решению задачи оперативного ситуационного анализа в организационных системах, it Управление при наличии расплывчатых категорий. Тезисы докладов IX научно - технического семинара.

Баку, 1987, с. 17-19.
[2] Алиев Р.А., Шахназаров М.М., Гулько Д.Е. Экспертная система для решения задач планирования непрерывных производств с нечетким представлением знаний. it Управление при наличии расплывчатых категорий: Тезисы докладов IX научно - технического семинара.

Баку, 1987, с. 43-46.
[3] Батыршин 11.3. О мерах энтропии размытых множеств. Исследование операций и аналитическое проектирование в технике.

Труды Казанского авиационного институтата. 1978, Вып.

1, с. 40 - 45.
[4] Веллман Р., Заде Л. Принятие решение в расплывчатых условиях. Вопросы анализа и процедуры принятия решений.

Пер. с англ. М., Мир, 1976, с. 172 -215.
[5] Берг А.И. Кибернетика - наука об оптимальном управлении.

М., ’’Энергия", 1964.
[6] Блишун А.Ф. Моделирование процесса принятия решений в нечетких условиях на основе сходства понятий классов.

Автореферат диссертации на соискание ученой степени кандидата физико-математических наук. М., ВЦ АН СССР, 1982, 19 с.
[7] Борисов А.Н., Осис Я.Я. Методика оценки функций принадлежности элементов размытого множества. Кибернетика и диагностика, Рига, PI III.

1970, с. 125-134.
[8] Брутян Г.А. Гипотеза Сепира - Уорфа. Ереван, 1968, 120 с.
[9] Величковчкий Б.М. it Современная когнитивная психология. М., Издательство МГУ, 1982, 336 с.
[10] Винер Н. Творец и робот. М., Прогресс, 1966, 255 с.
[11] Глушков В.М., Брановицкий В.И., Довгялло А.М. и др. Человек и вычислительная техника. Киев, Наукова думка, 1974, 294 с.
[12] Горелик А.Л., Гуревич И.Б., Скрипкин В.А. Современное состояние проблемы распознавания. М., Радио и связь, 1985, 98 с.
[13] Дюбуа , Прайд 1990 Теория, возможностей: Приложения к представлению знаний в информатике.
[14] Жуковин В.Е., Оганесян Н.А., Бурштейн Ф.В., Корелов Э.С. Об одном подходе к задачам принятия решений с позиций теории нечетких множеств. Методы принятия, решений в условиях неопределенности.

Рига: РПИ, 1980, с. 12-16.
[15] Журавлев ІО.І I. Об алгебраическом подходе к решению задач распознавания и классификации, it Проблемы кибернетики. 1978, Вып.

33, с. 28 - 57.
[16] Заде Л.А. Основа нового подхода к анализу сложных систем и процессов принятия решений. Математика сегодня. Под ред.

Н.Н. Моисеева, М., Знание, 1974, с. 5 - 48.
[17] Заде Л.А. Понятие лингвистической переменной и его применение к принятию приблизительных решений. М., Мир, 1976, 165 с.
[18] Заде Л.А. Размытые множества и их применение в распознавании образов и кластер-анализе. Классификация и кластер.

Под. ред. Дж.

Вэн Райзин, М., Мир, 1980, с. 208 - 247.
[19] Ильин В.А., Поздняк Э.Г. Основы, математического анализа. Частъ 1. М. Наука, 1982, 616 с.
[20] Киквидзе З.А., Ткемаладзе Н.Т. Об одном способе взвешивания элементов нечеткого множества.

Сообщения АН СССР, 1979, т. 93, 2, с. 317-320.
[21] Кофман А. Введение в теорию нечетких множеств. Пер. с франц. М., Радио и связь, 1982, 432 с.
[22] Кудрявцев В.Б., Алешин С.В., Подколзин А.С. Введение в теорию автоматов. Москва, ’’Наука", 1985, 319 с.
[23] Кузьмин В.Б. Построение групповых решений в пространствах четких и нечетких бинарных отношений. М., ВНИИСИ, 1982, 63 с.
[24] Ларичев О.И., Петровский А.Б. Системы поддержки принятия решений: современное состояние и перспективы развития. Итоги науки и техники. Серия "Техническая кибернетика".

Т. 21, М., ВИНИТИ, 1987, с. 18 - 35.
[25] Литвак Б.Г. Экспертная информация: методы получения и анализа. М., Радио и связь, 1982, 184 с.
[26] Ляпунов А.А. О некоторых общих вопросах кибернетики. ".Проблемы кибернетики", вып.1, 1959.
[27] Миркин Б.Г. Анализ качественных признаков и структур. М., Наука, 1982, 286 с.
[28] Модели принятия решений на основе лингвистической пе- ременной. Под ред. А.Н.

Борисова, А.В. Алексеева, О.А.

Крумберга. Рига, Зинатне, 1982, 256 с.
[29] Нечеткие множества в моделях управления и искусственного интеллекта. Под ред.

Поспелова Д.А. М., Наука, 1986, 311 с.
[30] Орловский С.А. Проблемы принятия, решений при нечеткой исходной информации. М., Наука, 1981, 208 с.
[31] Петров Б.Н., Уланов Г.М., Гольденблат И.И. и др. Информационные и термодинамические аспекты качественной теории эволюционных моделей развивающихся динамических систем управления. Итоги науки и техники.

Серия "Техническая кибернетика". Т.Ю., М., ВИНИТИ, 1978, с. 4 - 13.
[32] Попов Э.В. Экспертные системы: решение неформальных задач в диалоге с ЭВМ. М., Наука, 1987, 288 с.
[33] Построение экспертных систем,. Под редакцией Ф. Хейес-Рот, Д. Уотерман, Д. Ленат. М., Мир, 1987, 441 с.
[34] Представление знаний в человеке - машинных и робототехнических системах. Том С, М., ВИНИТИ, 1984, 412 с.
[35] Пфанцгаль И. Теория, измерений. Пер. с англ. М., ’’Мир", 1978
[36] Рубахин В.Ф. Психологические основы, обработки первичной информации. Ленинград, Наука, 1974, 518 с.
[37] Руспини Э.Г. Последние достижения в нечетком кластераанализе. Нечеткие множества и теория возможностей.

Последние достижения Под редакцией Рональда Р. Ягера, М., Радио и связь, 1986, с 47 - 62.
[38] Рыжов А.П., Аверкин А.Н. Аксиоматическое определение степени нечеткости лингвистической шкалы и ее основные свойства. II Всесоюзная, конференция ".Искусственный интеллект - 90" : Секционные и стендовые доклады,.

Том 1, Минск, 1990, с. 162 - 165.
[39] Рыжов А.П. Об одном методе выбора множества шкальных значений нечетких лингвистических шкал. Всесоюзная, конференция по искусственному интеллекту.

21 - 25 ноября, 1988 г.: Тезисы докладов. Том I, Переславль-Залесский, 1988, с. 521 - 525.
[40] Рыжов А.П. Об одном методе оптимального описания объектов и ситуаций в интеллектуальных системах.

Создание и применение гибридных экспертных систем,: Тезисы докладов Всесоюзной конференции, Ноябрь 1990 г., Рига, 1990, с. 62 - 64.
[41] Рыжов А.П. О степени нечеткости размытых характеристик. Математическая кибернетика, и ее приложения в биологии Под редакцией Л.В.Крушинского,
С.В.Яблонского, О.Б.Лупанова. М., Издательство МГУ, 1987, с. 60 - 77.
[42] Рыжов А.П. О степени нечеткости размытых характеристик.

Проблемы теоретической кибернетики: Тезисы докладов VII Всесоюзной конференции 18 сентября - 20 сентября 1985 г. I Часть, Иркутск, 1985, с 53 - 55.
[43] Рыжов А.П. Степень нечеткости лингвистической шкалы и ее свойства.

Нечеткие системы поддержки принятия, решений. Под редакцией Аверкина А.Н. и др., Калинин, Издательство Калининского госуниверситета, 1988, с. 82 - 92 .
[44] Рыжов А.П. Оценка степени нечеткости и ее применение в системах искусственного интеллекта. Интеллектуальные системы. Т.1, Вып.

1-1. Москва, МНЦ КИТ, 1996, с. 95 - 102.
[45] Садомов Ю.Б. О структурной организации и развитии диалоговых систем.

Человеко-машинные процедуры решения оперативных задач в АСУ. М., ДНТП, 1974, с. 12 - 17.
[46] Санчес Гуверне Ж., Бартолен Р., Вован Л. Лингвистический подход к нечеткой логике ВОЗ-классификации дисепотеинемии. Нечеткие множества и теория возможностей.

Последние достижения. Под редакцией Рональда Р. Ягера, М., Радио и связь, 1986, с. 173 - 182.
[47] Смете Ф. Простейшие семантические операторы. Нечеткие множества и теория возможностей.

Последние достижения. Под редакцией Рональда Р. Ягера, М., Радио и связь, 1986, с. 144 -158.
[48] Танака X., Цукияма Т, Асаи К. Модель нечеткой системы, основанная на логический структуре. Нечеткие множества и теория возможностей.

Последние достижения. Под редакцией Рональда Р. Ягера, М., Радио и связь, 1986, с. 63 - 75 .
[49] Тарасов В.Б., Перфильев С.А. О расстояниях между нечеткими множествами и их использовании в задаче принятия решений.

Управление при наличии расплывчатых категорий: Тезисы Y научно-технического сем,ина,ра. Пермь, 1982, с. 76 - 79.
[50] Ту Дж., Гонсалес Р. Принципы, распознавания образов. Пер. с англ., М., Мир, 1978, 411 с.
[51] Тэрано Т, Асаи К., Сугэно М. 1993 Прикладных нечеткие систем,ы.
[52] Фу К. Структурные методы в распознавании объектов. Пер. с англ.

М., ’’Мир", 1977.
[53] Человек и ЭВМ (психологические проблемы, автоматизации управления). Под редакцией Тихомирова О.К., М., Экономика, 1973, 183 с.
[54] Шапиро Д.И. Организационные систем,ы, управления: использование расплывчатых категорий. М., Энергоатомиздат, 1983, 117 с.
[55] Шер А.П. Согласование нечетких экспертных оценок и функция принадлежности в методе размытых множеств.

Моделирование и исследование систем автоматического управления, Владивосток, ДВНЦ АН СССР, 1978, с. 111-118.
[56] Шеридан Т.Б., Феррел У.Р. Системы человек - машина: модели обработки информации, управления и принятия, решений человеком, - оператором. Перевод с английского, М., Машиностроение, 1980, 520 с.
[57] Этнопсихолингвистика. Под редакцией Сорокина Ю.А., М., Наука, 1988, 92 с.
[58] Яблонский С.В. Основные понятия кибернетики. ’’Проблемы кибернетики", вып.2, 1959.
[59] Bauer Р., Klement Е., Leikermoser A., Moser В. Approximation of Beal Functions by Buie Bases. Proceedings of the Fifth International Fuzzy Systems Association World Congress, Seoul, Korea, 1993 V. 1, p. 239-242.
[60] Bezdek J.S. Numerical taxonomy with fuzzy sets. Journal of Mathematical Biology.

1974, v. 1, p. 57- 71.
[61] Bose P., Piver O. 1993 On, the evaluation of fuzzy quantified queries in a databases managment system.
[62] Braae M., Butherford D.A. Selection of parametrs for fuzzy logic controller.

Fuzzy Sets and Systems, 1979, V.2, p. 185-199.
[63] Bremermann H. Pattern recognition. Systems theory in the social sciences Ed. by H. Bossel at al.

Stuttgart: Binkhauser Verlag, 1976, p. 116-159.
[64] Buckles B.P., Petry F.E. Uncertainty models in, information and database systems Перевод: Модели неопределенности в информационных системах и базах данных. Экспресс-информация. Информатика.

1986, N 43, с. 11 - 14.
[65] СаросеШ В., De Luca A. Fuzzy sets and decision theory. Information, and Control.

1973, v.23, p. 43 - 50.
[66] Chang S.K. On the execution of fuzzy programs using finite state mashines. IEEE Transactions on Computers.

1972, v. 29, p. 15 - 21.
[67] Chu A.T.W., Kalaba B.E., Spingarn J. A comparison of two methods for determining the weights of belonging to fuzzy sets. Journal of Optimization Theory and Applications, 1979, V. 27, p. 531-538.
[68] De Luca A., Termini S. A definition of a non-probabilistic entropy in the setting of fuzzy set theory. Information, and Control.

1972, v.20, p. 301 - 312.
[69] De Luca A., Termini S. Measures of ambiguity in the analysis of complex systems. Lectures Notes on Computer Sciences.

1977, v. 53, p. 58 - 73.
[70] Di Nola A., Ventre A.G. Pointwice chois criteria determined by global properties.

BUSEFAL 1983, v.12, p. 97 - 112.
[71] Dubois D., Prade H. Algorithmes de puls courts chemins pour traiter des donnees flous. RAIRO.

Recherche Operationelle, 1978, v. 12, N 2, p. 213 - 227.
[72] Dubois D., Prade H. Decision-making under fuzziness. Advances in fuzzy set theory and applications, Ed. by M.M.

Gupta, E.K. Eagade, E.E.Jager, Amsterdam, North-Holland Publication Corporation, 1979, p. 279 - 302.
[73] Ebanks B.E. On measures of fuzziness and thier representation.

Journal of Mathematical Analysys and Applications. 1983, v. 94, p. 63 - 76.
[74] Fukami S., Mizumoto M., Tanaka K. Some considerations on fuzzy conditional inferences. Fuzzy Sets and Systems, 1980, v. 4, p. 243 - 273.
[75] Fuzzy Sets and Their Applications to Cognitive and Decision Processes Ed. by L.A. Zadeh et al. N.Y., Academic Press, 1975, 120 p.
[76] Goguen J.A. L-fuzzy sets.

Journal of Mahtematical Analysis and Applications. 1967, v.18, p. 145 - 174.
[77] Ishikawa A., Mieno H. The fuzzy entropy concepts and its application. Fuzzy Sets and Systems.

1979, v.2, p. 38 - 52.
[78] E. Krause, M. Schroder. An application of equality relations to idle speed control. - In: Proceedings of the First European Congress on Intelligent Technologies.

September 7-10, 1993. Aachen, Germany. - V.l. - pp.370-376.
[79] Mamdani E.H. Application of fuzzy ligic to approximate reasoning using linguistic systems.

IEEE Transaktion Computational, 1977, v. 26, p. 1182 - 1191.
[80] Mansfield W.H., Fleischman E.M. 1993 A high perfomance fuzzy query processing system for relational databases.
[81] Michinori, Nakata 1991 Integrity constraints in fuzzy databases
[82] Mizumoto M., Fukami S., Tanaka K. Fuzzy conditional inferences and fuzzy inferences with fuzzy quantifiers. Proceedings of the International Conference on Artificial Intelligence, Tokyo, 1979, p. 20 - 23.
[83] Mizumoto M., Tanaka K. Algebraic properties of fuzzy numbers. Proceegings of IEEE International Conference on Cybernetisc and Society, 1976, p. 559 - 563.
[84] Mizumoto M., Tanaka K. Some properties of fuzzy numbers. Advances in fuzzy set theory and applications, Amsterdam, North-Holland Publication Corporation, 1979, p. 153 - 164.
[85] Mizumoto M., Zimmermann H.J. Comparison of fuzzy reasoning methods.

Fuzzy Sets and Systems, 1982, v.8, p. 253 - 283.
[86] Negoita C.V., Ealescu D.A. Applications of fuzzy sets to systems analysis. Basel, Birkhauser Verlag, 1975, 178 p.
[87] Osgood C.E., Suci G.L., Tannenbaum P.H. The measurement of meaning.

University of Illinois Press, Urbana, 1957, p. 1-342.
[88] Pollatschek M.A. Hierarchical systems and fuzzy set theory.

Kybernetes. 1977, v.6, p. 43 - 57.
[89] Prade H. Using fuzzy set theory in scheduling problem: a case study. Fuzzy Sets and Systems, 1979, v. 2, N 2, p. 153 - 165.
[90] Eagade E.K., Gupta M.M. Fuzzy sets theory: introduction.

Fuzzy Automata and Decision Processes Ed. by Gupta M.M., Saridis G., Gaines B. Amsterdam: North-Holland, 1977, p. 105-131.
[91] Eaymond C., Boverie S., Le Quebec J.M. Practical realisation of fuzzy controllers comparison with conventional methods. Proceedings of the First European Congress on Intelligent Technologies. September 7-10, 1993.

Aachen, Germany. V.l. - pp.149156.
[92] Eiera T., Trillas E. From measures of fuzziness to booleanity control. Fuzzy Information and Decision Processes.

Ed. by M.M. Gupta, E. Sanchez.

Amsterdam, North-Holland, 1982, p. 67 - 82.
[93] Ryjov A.P. The axiomatic definition of a linguistic scale fuzziness degree, its major properties and applications. North American Fuzzy Logic Proceeding Society (NAFIPS!92).

Proceedings of a Conference held in PUERTO VALLARTA, MEXICO, December 15-17, 1992. NASA Conference Publication 10112, Vol.

1, p. 21-29.
[94] Ryjov A. The measure of uncertainty of fuzzy set’s collection: defenition, properties and applications. Proceedings of ISUMA’93. The Second International Symposium on Uncertainty Modeling and Analysis. - University of Maryland, College Park, Maryland, USA, April, 25-28, 1993.

IEEE COMPUTER SOCIETY PRESS, p. 3742.
[95] Ryjov A. The Information Retrieval in Fuzzy Data Bases. Proceedings of the Fifth International Fuzzy Systems Association World Congress’93. - July f-9, 1993, Seoul, Korea.

Vol.l, p. 477 - 480.
[96] Ryjov A. Fuzzy data bases: description of objects and retrieval of information. Proceedings of the First European Congress on Intelligent Technologies. September 7-10, 1993. Aachen, Germany.

V.3, p. 1557-1562.
[97] Ryjov A. The Concept of a Full Orthogonal Semantic Scope and the Measuring of Semantic Uncertainty. Fifth International Conference Information Processing and Management of Uncertainty in Knowledge-Ва- sed Systems. - Paris, July f-8, 199f. p. 33-34.
[98] Ryjov A. and Loginov D. On the Choice of an Optimal Value-Set of Qualitative Attributes for Information Retrieval in Data Bases. Fuzzy Logic and Intelligent Technologies in Nuclear Science - Proceedings of the 1st International FLINS
Workshop Mol, Belgium, September 14-16, 1994- Edited by Da Euan, Pierre D’hondt, Paul Govaerts, Etienne E. Kerre. World Scientific, p. 58-62.
[99] Eyjov A. The Practical Use of the Technique of Choosing an Optimal Value-Set of Qualitative Attributes: the Problem of Stability. Fuzzy Logic and Intelligent Technologies in Nuclear Science - Proceedings of the 1st International FLINS Workshop Mol, Belgium, September 14-16, 1994- Edited by Da Euan, Pierre D’hondt, Paul Govaerts, Etienne E. Kerre.

World Scientific, p. 63-66.
[100] Lyapin B. and Eyjov A. A Fuzzy Linguistic Interface for Data Bases in Nuclear Safety Problems. Fuzzy Logic and Intelligent Technologies in Nuclear Science -Proceedings of the 1st International FLINS Workshop Mol, Belgium, September lf-16, 1994- Edited by Da Euan, Pierre D’hondt, Paul Govaerts, Etienne E. Kerre.

World Scientific, p. 212-215.
[101] Belenki A. and Eyjov A. Fuzzy Logic in Monitoring the Non-Spread of Nuclear Weapons. Fuzzy Logic and Intelligent Technologies in Nuclear Science - Proceedings of the 1st International FLINS Workshop Mol, Belgium, September 14-16, 1994-Edited by Da Euan, Pierre D’hondt, Paul Govaerts, Etienne E. Kerre.

World Scientific, p. 219-222.
[102] Kudrjavcev V., Eyjov A., Kozlov V. and A. Strogalov A. An Expert System for the Evaluation of the Negative Effects of Environment on Person During the Liquidation of Nuclear, Industrial and Ecological Accidents. Fuzzy Logic and Intelligent Technologies in Nuclear Science - Proceedings of the 1st International FLINS Workshop Mol, Belgium, September 14-16, 1994- Edited by Da Euan, Pierre D’hondt, Paul Govaerts, Etienne E. Kerre.

World Scientific, p. 266-270.
[103] Eyjov A. Optimal Description of Objects in Human-Machine Information Systems. Application of Fuzzy Systems - Proceedings of the International Conference on Application of Fuzzy Systems - ICAFS-94 held at the University of Tabriz, Tabriz, Iran, October 17-19, 1994- P- 246-249.
[104] Eyjov, A., Belenki, A., Hooper, E., Pouchkarev, V., Lai I ah. A. and Zadeh, L.A. Development of an Intelligent System for Monitoring and Evaluation of Peaceful Nuclear Activities (DISNA), IAEA, STE-310, Vienna, 1998, 122 p.
[105] Eueda A., Pedrycz W. Fuzzy Coordinator in Control Problems. North American Fuzzy Logic Processing Society (NAFIPS’92).

Proceedings of a Conference held in PUERTO VALLARTA, MEXICO, December 15-17, 1992, NASA Conference Publication 10112, V. 1, p. 322-329.
[106] Euspini E.H. A new approach to clustering.

Information and Control. 1969, v.2, p. 22 - 32.
[107] Euspini E.H. Numerical methods for fuzzy clustering Information Sciences.

1970, v.2, p. 319 - 350.
[108] Saaty T.L. Exploring the interface between hierarchies, multiple objectives and fuzzy sets.

Fuzzy Sets and Systems, 1978, V.l, p. 57-69.
[109] Saaty T.L. Measuring the fuzziness of sets.

Journal of Cybernetics, 1974, V.4, p. 53-61.
[110] Sanchez E. Inverses of fuzzy relations. Applications to possibility distribution and medical diagnosis.

Fuzzy Sets and Systems, 1979, V.2, p.75-86.
[111] Skala H.J. On many-valued logic, fuzzy logic and their applications.

Fuzzy Sets and Systems, 1978, V.l, p. 129-149.
[112] Thole U., Zimmermann H.J., Zysno P. On the suitability of minimum and products operators for the intersection of fuzzy sets. Fuzzy Sets and Systems, 1979, p. 1-14.
[113] Zadeh L.A. Approximate reasoning in in fuzzy logic.

Proceedings of the International Conference on Artificial Intelligence, Tokyo, 1979.
[114] Zadeh L.A. A theory of approximate reasoning.

Machine Intelligence, 1979, v.9, p. 149 - 194.
[115] Zadeh L.A. Calculus of fuzzy restrictions. Fuzzy Sets and Their Applications to Cognitive and Decision Processes, Ed. by Zadeh L.A. and al.

New York: Academic Press, 1975, p. 1-41.
[116] Zadeh L.A. Fuzzy logic and approximate reasoning.

Synthese, 1975, v. 80, p. 407 -428.
[117] Zadeh L.A. Fuzzy sets.

Information and Control, 1965, v.8, p. 338 - 353.

Содержание раздела

---