Рыжов А. - Элементы теории нечетких множеств и ее приложений
Предисловие
Любая наука занимается изучением определенных моделей реального мира. Даже описывая что-то словами, мы на самом деле формулируем модель некоторого реального объекта, события и т.п. на естественном языке.
Соотношение реального объекта и его модели - старый философский вопрос, который можно сформулировать как проблему соотношения некоторого объекта и нашего знания о нем. На эту тему написано огромное количество книг, но мы не будем заниматься этими проблемами.
Отметим лишь, что при рассмотрении этого вопроса почти все философские школы сходятся в одном: модель есть не совсем точное описание объета (’’грубое", ’’исаженное" и т.п.).
Итак, модель не есть эквивалент объекта. Модель всегда является более бедной.
Поэтому в модели присутствует неопределенность, которую необходимо учитывать при переносе выводов, полученных при ее анализе, на реальный объект.
Мы упомянули очень важное слово неопределенность. Это также сложное философское понятие.
Мы затронем его лишь на уровне структуры понятия. Можно привести следующую классификацию неопределенности (Рис.
1).
Отметим, что разные типы неопределенности имеют средства поддержки обработки информации, обладающей ими (Рис. 1).
Физическая неопределенность описывает неопределенность объектов реального мира с точки зрения наблюдателя. Так, неточность связана с возможностями измерительного оборудования. Например, если мы имеем шкалу с шагом 1 мм., мы не можем измерять размеры с точностью до микрона.
В этом случае мы можем говорить о размерах с определенной точностью. Математической моделью обработки такого типа неопределенность является интервальная арифметика. С объектами, из-мерянными в различных шкалах, мы должны работать по-разному.
Например, для ранговых или номинальных шкал арифметические операции (включая вычисление средних значений) не имеют смысла. Изучение подобных вопросов составляет предмет исследования теории измерений [35].
Теория вероятностей имеет дело с неопределенностью некоторых событий. Мы, например, можем спросить: ’’Какова вероятность того, что выйдя на улицу мы встретим человека роста 2 м.?" Ответ на этот вопрос зависит от распределения людей по росту (вобще говоря, в данном конкретном городе).
Теория вероятностей, имеющая более 200 - летнюю историю, представляет, пожалуй, наиболее развитую теорию, ориентированную на обработку неопределенности. Однако, и это необходимо понимать, эта теория базируется на ряде предположений и гипотез, без проверки которых для данной конкретной проблемы мы не можем гарантировать адекватность выводов, полученных в рамках анализа модели, реальным объектам или процессам. Примерами таких требований могут быть:
- повторяемость событий;
- гарантии того, что наблюдаемые эффекты могут быть перенесены на все объекты или события данного типа (генеральную совокупность);
-независимость событий и т.п.
Теория формальных грамматик изучает неопределенность смысла фраз. Примером такого рода неопределенности может быть известное высказывание ’’Казнить нельзя помиловать". В зависимости от расположения запятой, смысл фразы меняется на противоположный.
Язык формальных грамматик оказался очень удобным для решении ряда практических задач, например, в рамках распознавания образов [52].
Теория нечетких множеств есть некоторый аппарат формализации одного из видов неопределенности, возникающей при моделировании (в широком смысле этого слова, не только математическом) реальных объектов. Нечеткость возникает всегда, когда мы используем слова естественного языка при описании объекта. Последнее возникает всегда, когда мы пытаемся применять информационные технологии в " нетрадиционных" или ’’гуманитарных" областях, таких как медицина, экономика, управление (с участием или учетом свойств лица, принимающего решения), социология и пр.
В рамках теории нечетких множеств разработан аппарат формализации содержательно значимых понятий, примерами которых являются ’’человек среднего роста", ’’устойчивая ситуация", ’’высокий уровень безопасности" и т.п.
Данная монография написана на основе курса лекций, который читался в течение ряда лет для студентов 2-5 курсов механико-математи-ческого факультета и факультета вычислительной математики и кибернетики МГУ им. М.В.
Ломоносова.
Несмотря на значительный ’’возраст" теории нечетких множеств (первая статья по этому вопросу была опубликована в 1965 году [117]), систематизированное изложение некоторых ее аспектов в виде курса лекций для студентов математических факультетов МГУ им. М.В.
Ломоносова было предпринято в начале 90-х годов. Этому может быть много объяснений, основное из которых - значительное развитие прикладной части данного направления и относительная неразвитость математических основ.
К учебной литературе по теории нечетких множеств, изданной на русском языке, можно отнести лишь известную книгу ныне покойного А. Кофмана [21]. Это издание - первая из его четырех книг. Остальные, к сожалению, так и не были переведены на русский язык. Однако она, как отмечает автор, ориентирована на инженеров и студентов инженерных специальностей.
Поэтому настоящий монография имеет своей целью заполнить имеющийся пробел в данной области.
В работе вводятся и описываются свойства лишь основных объектов теории нечетких множеств: собственно понятие нечеткого множества, свойства множества нечетких подмножеств универсального множества, нечеткие отношения и некоторые их свойства, модели приближенных рассуждений. Основное внимание уделяется описанию методов измерения неопределенности нечетких объектов.
Формулируются проблемы в этой области, не нашедшие своего решения в настоящее время. Систематизированное изложение этих аспектов теории нчетких множеств, имеющих важное значение как для теории так и для ложений нечетких систем (см., например, [104]), приводится впервые в научной литературе.
Это является второй целью выпуска данной работы.
Пользуясь случаем, автор хотел бы поблагодарить сотрудников кафедры математической теории интеллектуальных систем и лаборатории проблем теоретической кибернетики механико - математического факультета МГУ им. М.В. Ломоносова и кафедры математической кибернетики факультета вычислительной математики и кибернетики за обсуждение структуры курса, весьма ценные замечания и поддержку при подготовке данной монографии. Заведующий кафедрой математической теории интеллектуальных систем и лаборатории проблем теоретической кибернетики академик АТН РФ профессор Валерий Борисович Кудрявцев многократно перечитывал рукопись; его советы, ремарки и замечания значительно изменили содержание и текст в лучшую сторону.
Я хотел бы выразить искреннюю признательность Валерию Борисовичу за эту большую и кропотливую работу.
Выпуск данной работы стал возможет лишь при финансовой поддержке Федеральной Целевой Программы ’’Интеграция". В рамках проекта 431 (направление 2.1) ’’Создание совместного научно-учебного центра ’’Интеллектуальные системы и нечеткие технологии", объединяющего ученых и преподавателей МГУ им.
М.В. Ломоносова, ВЦ РАН и РГГУ, происходит чрезвычайно интересный и полезный для всех участников обмен идеями и результатами, формулируются и решаются новые задачи, читаются новые курсы лекций. Подготовка и выпуск данной монографии -один из результатов такой совместной работы. Ее концепция и содержание неоднократно обсуждались с директором центра компьютерных технологий в образовании профессором А.С.
Строгановым и заместителем заведующего отдела искусственного интеллекта ВЦ РАН членом - корреспондентом МАИ А.Н. Аверкиным.
Автор хотел бы искренне поблагодарить их за полезное обсуждение работы и поддержку.
А.П. Рыжов.
Нечеткие множества и их свойства
Понятие нечеткого множества
Следуя Заде [117], введем понятие нечеткого множества следующим образом.
Пусть U - некоторое множество элементов и, и ца : U ^ [0,1]. Нечетким подмножеством A в U называется график отображения /іа-, то есть множество вида {(и, ia(u)) : и ? U}; при этом значение Ia(u) называется степенью принадлежности и к A.
Таким образом, задание нечеткого подмножества A в U эквивалентно заданию его функции принадлежности Ia(u). Мы, следуя сложившейся традиции, будем употреблять темин ’’нечеткое множество" вместо более корректного термина ’’нечеткое подмножество".
Приведенное определение нечеткого множества является довольно общим. Поэтому при анализе и синтезе нечетких систем используются различные его частные случаи.
Приведем два примера нечетких множеств, точнее, функций принадлежностей, соответствующих им. Ими являются так называемые s и п функции, задаваемые так:
| S(и; а, в, y) |
|
S(и; y e,Y f ,Y) для: и Y, S(и; y,Y + f ,Y + в) для: и Y-
п(и; e,Y)
(1.2)
Их графики имеют вид, как указано на рис. 1.1 и 1.2.
Для частного случая, когда U является подмножеством числовой прямой, часто используются нечеткие множества (L R) типа [72], [29]. Функции принадлежности для таких множеств задаются с помощью функций L и R, удовлетворяющих следующим требованиям:
1) L(0) = R(0) = 1;
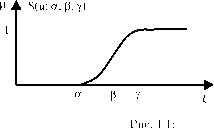
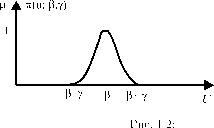
2) L и R - невозрастающие функции на множестве неотрицательных действительных чисел.
Пример 1 Примеры, функций L и R.
1) L(u) = e-\u\,p 0;
u\P '
1 npи u E [1,1],
0 в противном случае
Ю R(u) = i+U\p ,rP
3) L(u)
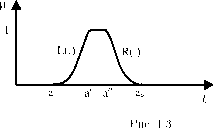
Функция принадлежности нечеткого множества A, имеющая (L R) тип, задается так:
{L ус-) ПРИ u a', aL 0;
R (uO)) При u a, an 0; (L3)
1 при u E [a1, a"}.
Иногда отрезок [a', a] называют интервалом толерантности, a aL и an - левым и правым коэффициентом нечеткости соответственно. Пример функции принадлежности (L R) типа представлен на рис. 1.3.
Функции принадлежности s и п типа являются частным случаем функций (L R) типа.
Другим примером функций принадлежности (L R) типа, используемых нами далее, доставляет предположение, что L и R являются линейными. В этом случае имеем:
0 при u aL;
u-aL
а'-аь
1 при a1 u a';
aR-u
aR-a''
0 при u an.
при aL u a'; при a u an;
Pa(u)
(1,4)
Такие функции принадлежности называем линейными функциями принадлежности L R типа. Пример линейной функции принадлежности L R типа представлен на рис. 1.4.
Линейные функции принадлежности L R типа при a' a'' называются трапецеидальными, при a' = a'' = a - треугольными.
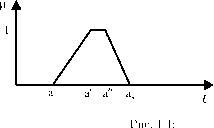
Как можно обобщить понятие нечеткого множества? Прежде всего, обобщение каснулось множества, описывающего степень принадлежности, т.е. множества [0,1]. Использование этого интервала для оценки степени принадлежности вполне естественно из-за наглядной интерпретации: 0 - полная непринадлежность элемента универсума нечеткому множеству, 1- его полная принадлежность. Однако, интерпретация является является делом вкуса и может кому-то нравиться, а кому-то - нет. Так, в экспертной системе МУСIX [33] в качестве интервала, описывающего неопределенность, используется [-1,1]. Это объясняется большой важностью значения с максимальной неопределенностью, которое при данном выборе множества принадлежностей равно 0. В качестве множества принадлежностей рассматривались также [0,10], {0,0.1,0.2,..., 0.9,1}, множество неотрицательных действительных чисел, полные дистрибутивные решетки, упорядоченные полукольца и т.п. [29], [21]. От множества принадлежностей мы можем потребовать лишь одно: мы должны иметь возможность сравнивать принадлежность различных элементов универсума нечеткому множеству, т.е. на элементах множества принадлежности должно быть задано отношение порядка.
Таким образом, определение нечеткого множества (с. 9) можно обобщить следующим образом.
Пусть U - обычное множество, М - множество принадлежностей, цл : U ^ М. Нечетким множеством A в U называется график отображения цЛі то есть множество
ВИДЯ
{(п,^л(и)) : и Е U},
Таким образом, нечеткое множество A задается тройкой
(U, M,va).
Множество нечетких подмножеств U и его свойства
Обозначим через V(U) множество всех нечетких подмножеств U. Опишем некоторые свойства V(U).
Прежде всего заметим, что мощность V(U) выше мощности множества подмножеств U. Действительно, если мощности множеств U и М конечны, то есть \U\ = n, \M\ = m, то \P(U)| = mn. При m = 2 (обычные множества) \P(U)| = 2n - число подмножеств U.
Основные теоретико-множественные операции в P(U) вводятся следующим образом.
Говорят, что нечеткие множества A и B равны (A = B), если для всех и из U выполнено на(и) = Нв(и).
Говорят, что нечеткое множество A включает нечеткое множество B (A D B), если для всех и из U выполнено нВ(и) Ha(u).
Говорят, что нечеткое множество B является дополнением нечеткого множества A в U (B = A), если для всех и из U выполнено нВ(и) = 1 Ha(u).
Говорят, что нечеткое множество С является пересечением нечетких множеств A и B (С = A П B), если для всех и из U выполнено Нс (и) = тіп{НА(и),Нв (и)}.
Говорят, что нечеткое множество С является объединением нечетких множеств A и B (С = A U B), если для всех и из U выполнено нС(и) = тах.{нА(и), Нв(и)}.
Говорят, что нечеткое множество С является алгебраическим произведением нечетких множеств An B (С = A*B), если для всех и из U выполнено нС (и) = Ha(u)hb (и).
Говорят, что нечеткое множество С является алгебраической суммой нечетких множеств A и B (С = A+B), если для всех и из U выполнено нС(и) = Ha(u) + Нв(и) Ha(u) - Нв(и).
Нетрудно видеть, что замена в этих определениях функции принадлежности Н(и) на характеристическую функцию приводит к обычным операциям с теми же названиями в теории множеств.
Напомним, что алгеброй называется множество с определенными на его элементах операциями. Рассмотрим множество P(U) и определенные на его элементах и их парах операции дополнения, пересечения и объединения.
Будем обозначать такую алгебру (P(U); П, U). Для нее справедливы следующие свойства.
| A П B = B П A, | (1.5) |
| A U B = B U A. | (1.6) |
| (A П B) П С = A П (B П С), | (1.7) |
| (A U B) U С = A U (B U С). | (1.8) |
| A П A = A, | (1.9) |
| A U A = A. | (1.10) |
| (A) = A. | (1.11) |
Утверждение 1 Для нечетких множеств А,В и C выполнено
А П (В U C) = (А П В) U (А П C), (1.12)
A U (В П C) = (A U В) П (A U C). (1.13)
Доказательство. Докажем равенство ( 1.12).
В соответствии с определениями равенства, пересечения и объединения нечетких множеств (с. 13), необходимо доказать, что для любого и из U выполнено
min{^A(u), max(^B(и),^с(и))} =
(1,14)
= max{min(^A(u), fiB(и)), min(^A(u), fiC(и))}
Зафиксируем некоторую точку и Е U.
Пусть a = цл(и), b = цв(и), c = цс(и). Возможны следующие варианты:
1) a b c; 2) a b = c; 3) a = b c; 4) a = b = c;
5) a c b; 6) a c = b; 7) a = c b; 8) b a c;
9) b a = c; 10) b c a; 11) b c = a; 12) b = c a;
13) c a b; 14) c a = b; 15) c b a.
Проверим выполнение формулы ( 1.14) в каждом из 15 случаев:
1) min{a,max(b,c)} = min{a,b} = b; max{min(a, b), min(a,c)} = max{b,c} = b.
Таким образом, ( 1.14) в случае 1) справедливо.
2) min{a, max(b, c)} = min{a, b} = b = c; max{min(a, b), min(a, c)} = max{b, c} = b = c.
Таким образом, ( 1.14) в случае 2) справедливо.
3) min{a, max(b, c)} = min{a, b} = b = a; max{min(a, b), min(a, c)} = max{b, c} = b = a.
Таким образом, ( 1.14) в случае 3) справедливо.
4) min{a, max(b, c)} = min{a, b} = a = b = c; max{min(a, b), min(a, c)} = max{a, a} = a = b = c.
Таким образом, ( 1.14) в случае 4) справедливо.
5) min{a, max(b,c)} = min{a,b} = a; max{min(a, b), min(a,c)} = max{a, c} = a.
Таким образом, ( 1.14) в случае 5) справедливо.
6) min{a, max(b,c)} = min{a,b} = a; max{min(a, b), min(a,c)} = max{a, a} = a.
Таким образом, ( 1.14) в случае 6) справедливо.
7) min{a, max(b,c)} = min{a,c} = c; max{min(a, b), min(a,c)} = max{b,c} = c.
Таким образом, ( 1.14) в случае 7) справедливо.
8) min{a, max(b, c)} = min{a, b} = b = c; max{min(a, b), min(a, c)} = max{b, c} = b = c.
Таким образом, ( 1.14) в случае 8) справедливо.
9) min{a, max(b,c)} = min{a,c} = a = c; max{min(a, b), min(a, c)} = max{b, a} = a = c.
Таким образом, ( 1.14) в случае 9) справедливо.
10) minja, max(b, c)} = minja, b} = a; maxjmin(a, b), min(a,c)} = maxja, a} = a.
Таким образом, ( 1.14) в случае 10) справедливо.
11) minja, max(b, c)} = minja, b} = a = c; max{min(a, b), min(a,c)} = maxja, a} = a = c.
Таким образом, ( 1.14) в случае 11) справедливо.
12) minja, max(b, c)} = minja, b} = a; max{min(a, b), min(a,c)} = maxja, a} = a.
Таким образом, ( 1.14) в случае 12) справедливо.
13) minja, max(b, c)} = minja, c} = a; maxjmin(a, b), min(a,c)} = maxjb,a} = a.
Таким образом, ( 1.14) в случае 13) справедливо.
14) minja, max(b, c)} = minja, c} = a = b; maxjmin(a, b), min(a,c)} = maxja, a} = a = b.
Таким образом, ( 1.14) в случае 14) справедливо.
15) minja, max(b, c)} = minja, c} = a; maxjmin(a, b), min(a,c)} = maxja, a} = a.
Таким образом, ( 1.14) в случае 15) справедливо.
Второе равенство ( 1.13)доказывается аналогично. Утверждение доказано.
Утверждение 2 Для нечетких множеств A и B выполнено
A П B = A U B, (1.15)
A U B = A П B. (1.16)
Это утверждение называется теоремой де Моргана.
Доказательство. Докажем равенство ( 1.15).
В соответствии с определениями равенства, пересечения, объединения и дополнения нечетких множеств (с. 13), необходимо доказать, что для любого и из U выполнено
1 minjpA(u),pB (u)} = maxjl pA(u), 1 рв (и)} (1.17)
Зафиксируем некоторую точку и Е U.
Пусть a = pa(u), b = рв(и). Возможны следующие варианты:
1) a b; 2) a = b; 3) b a.
Проверим выполнение формулы ( 1.17) в каждом из 3 случаев:
1) 1 minja, b} = 1 b; maxjl a, 1 b)} = 1 b. Таким образом, ( 1.17) в случае
1) выполнено.
1) 1 minja, b} = 1 a; maxj1 a, 1 b)} = 1 a. Таким образом, ( 1.17) в случае
2) выполнено.
1) 1 minja, b} = 1 a; maxj1 a, 1 b)} = 1 a. Таким образом, ( 1.17) в случае
3) выполнено.
Утверждение доказано.
Пустое множество, не содержащее ни одного элемента и обозначаемое 0, играет очень большую роль в теории множеств и логике. В случае нечетких множеств функция принадлежности пустого множества имеет следующий вид:
ц$(п) = 0 Уп Е U. (1.18)
Легко устанавливаются соотношения
A П 0 = 0, (1.19)
A U0 = A. (1.20)
Операции с универсальным множеством, то есть множеством, содержащим все элементы U, также играют особую роль в теории множеств и логике. В случае нечетких множеств функция принадлежности универсального множества имеет следующий вид:
| fiu (u) = 1 Уп Е U. | (1.21) | |
| Легко устанавливаются соотношения | ||
| A П U = A, | (1.22) | |
| A U U = U. | (1.23) | |
| Напомним, что, если F - обычное множество, то F П F = 0,F U F = U. Используя определения дополнения, пересечения и объединения для нечетких множеств (с. 13) не трудно показать, что для нечеткого множества A, для которого Зп Е U : 0 Цл(п) 1 данные соотношения не выполняются. Таким образом, в общем случае для нечеткого множества A справедливо | ||
| A П A = 0, | (1.24) | |
| A U A = U, | (1.25) |
Для алгеры (V(U); *, +) легко проверяются свойства коммутативности, ассоциативности, инволюции, теоремы де Моргана и соотношения с 0 и U. Аналоги соотношений 1.24 и 1.25, как и в случае (V(U); П, U), не выполняются.
Свойства коммутативности, инволюции и ассоциативности для алгебраического произведения является прямым следствием определений и соответствующих свойств операций умножения и сложения для чисел.
В некоторой дополнительной проверке могут нуждаться свойства ассоциативности для алгебраической суммы и теоремы де Моргана для указанных операций. Докажем первое из них.
Утверждение 3 Для нечетких множеств A, В и C выполнено
(A+В)+C = A+(B+C).
Доказательство. В соответствии с определениями равенства и алгебраической суммы нечетких множеств (с. 13), необходимо доказать, что для любого и из U выполнено
(Ма (и) + = ма (и) +
(1.26)
Мб (и) Ma(u) ¦ Мб (и)) + Мо (и)
(Ma(u) + Мб (и) Ma(u) ¦ Мб (и)) ¦ Мо (и) -(Mb (и) + Мо (и) Mb (и) ¦ Мо (и))
(Ma(u) ¦ (мб (и) + Мо (и) Mb (и) ¦ Мо (и))
Зафиксируем некоторую точку и Е U.
Пусть a = ma(u), b = мВ(u),c = мо(и)-
Тогда правая часть ( 1.26) равна (a + b a ¦ b) + с (a + b a ¦ b) ¦ c = a + b + c a ¦ b a ¦ с b ¦ с + a ¦ b ¦ с.
Левая часть ( 1.26) равна a+(b+cb^c)a\b+cb^c) = a+b+cb^ca^ba^c+c^b^c.
Сравнивая правые части последних двух равенств, получаем выполнение ( 1.26).
Утверждение доказано.
Доказательство теорем де Моргана для рассматриваемой алгебры читателю предлагается провести самостоятельно по схеме доказательства утверждения 3.
Новое в этой алгебре - невыполнение свойств идемпотентности и дистрибутивности. Первое является прямым следствием определения и свойств арифметических операций для чисел.
Докажем невыполнение дистрибутивности алгебраической суммы относительно алгебраического произведения.
Утверждение 4 Для нечетких множеств A, B и C выполнено
A * (B+C) = (A * B)+(A * C) (1.27)
Доказательство. Выберем и из U, и, полагая a = ma(u), b = мВ(u), c = Me(u), получим для, соответственно, левой части ( 1.27) a(b + с be) = ab + ac abc и правой части ( 1.27) ab + ae (ab)(ae).
Таким образом, правая и левая части ( 1.27) равны, если только a2 = a. Утверждение доказано.
Недистрибутивность алгебраического произведения относительно алгебраической суммы доказывается аналогично.
Справедливы также следующие свойства
| A * (B П C) = (A * B) П (A * C) | (1.28) |
| A * (B U C) = (A * B) U (A * C) | (1.29) |
| A+(B П C) = (A+B) П (A+C) | (1.30) |
| A+(B U C) = (A+B) U (A+C) | (1.31) |
Таким образом, для алгебры {V(U); П, U) в отличие от алгебры обычных подмножеств не выполняются операции с дополнением, для алгебры {V(U); *, +), кроме того, не выполняются идемпотентность и дистрибутивность.
Подмножества а - уровня. Декомпозиция нечетких множеств
Здесь устанавливается связь между нечетким подмножеством универсального множества U и определенным образом устроенном семейством обычных его подмножеств. Эта связь вводится при помощи понятия подмножества а - уровня нечеткого множества.
Пусть а Е [0,1]. Подмножеством а - уровня нечеткого множества А называется множество
Аа = {и Е U : рл(и) а}.
Утверждение 5 (О декомпозиции). Любое нечеткое множество А можно представить в виде
А = max а х Аа.
а
Доказательство. Обозначим через B нечеткое множество с функцией принадлежности рв(и) = maxa а х Аа(и). Зафиксируем некоторую точку и Е U. Пусть рл(и) = а. Тогда при а а и f3 а, соответственно, имеем рла (и) = 1 и рлв (и) = 0. Таким образом, maxa а х Аа(и) = рв(и) = а.
Итак, при и Е U имеем рл(и) = рв(и), что означает равенство множеств А и B.