Основные идеи нечеткого управления
Основные понятия теории управления
Понятие управления составило основу кибернетики как науки об общих законах управления и связи в живых и технических системах [10].
Концептуальная схема, в рамках которой формулируется любая задача управления, может быть представлена следующим образом (рис. 3.1).
Система управления на основе наблюдений среды и объекта управления и соответствия этих наблюдений цели формирует решение по выбору управляющего воздействия на объект (в частном случае это может быть ’’пустое" решение). Если при сложившейся ситуации в среде и на объекте управления цель достигнута - продолжается наблюдение за средой и объектом. Если цель не достигается - необходимо некоторое воздействие на объект.
Это воздействие выбирается блоком принятия решений на основе модели среды и модели объекта управления и выполняется блоком реализации решений. Воздействие вызывает переход объекта в новое состояние и, как следствие, некоторые возмущения в среде.
Новое состояние пары ’’объект управления - среда" может быть ближе к цели или, наоборот, удалять нас от нее. Мы можем оценить это, наблюдая объект и среду и сравнивая сложившуюся реальную ситуацию с целью.
Результат такого наблюдения и сравнения инициирует либо новые решения в случае, когда цель не достигается, либо пассивное наблюдение в случае, когда цель достигнута.
Различные аспекты представленной концептуальной схемы изучаются различными теориями. Так, например, связи между объектом и системой управления, как и связи между средой и системой управления, изучаются в рамках теории кодирования или, более широко, теории информации; выбор разумного (оптимального, целесообразного) решения составляет основную задачу теории принятия решений;
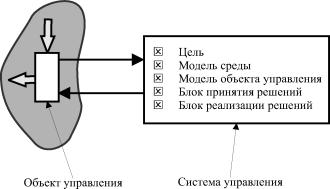
Рис. 3.1:
теория автоматов, теория игр. теория оптимального управления и многие другие -это углубленное изучение различных аспектов этой схемы.
Выделяются различные типы задач управления. Например, в [10] описываются задачи стабилизации, выполнения программы, слежения и оптимизации.
Даже краткий обзор подобных исследований может занять слишком много места, поэтому ниже основное внимание уделяется не столько описанию таких задач и методов их решения. сколько требованиям к описанию основных элементов управляющей системы (’’языку" формализации) в классических постановках задач.
Цель. В классических постановках задач управления предполагается, что цель задается в виде некоторой функции (например, в задачах слежения и выполнения программ), некоторой области заданных значений контролируемого параметра (задачи стабилизации), вероятности наступления некоторого события (например, вероятность поражения цели должна быть не ниже 0.999).
Имея такое представление цели и описание системы и среды в виде аналогичных объектов (функций и/или точек в некотором пространстве), мы имеем возможность сравнивать сложившуюся ситуацию на объекте управления с целью с помощью расстояние в некотором пространстве.
Модель среды и модель объекта управления.
В классическом понимании понятие модели основывается на наличии некоторого сходства между двумя объектами. При этом слова ’’сходство" и ’’объект" понимаются в очень широком смысле.
Сходство может быть чисто внешним, оно может относиться к внутренней структуре внешне совсем непохожих объектов или к определенным чертам поведения объектов, не имеющим ничего общего ни по форме, ни по структуре. Считается, что, если между двумя объектами может быть установлено сходство в каком- либо смысле, то между этими объектами существует отношение оригинала и модели.
Это означает, что один из этих объектов может рассматриваться как оригинал, а второй - как его модель.
Для кибернетических систем наиболее важным сходством между системами, приводящим к отношению ’’оригинал - модель" является сходство их поведения.
Математической моделью системы называется ее описание на каком-либо формальном языке, позволяющее выводить суждение о некоторых чертах поведения этой системы при помощи формальных процедур над ее описанием. Виды математических моделей, используемые в качестве моделей среды и объекта управления, весьма разнообразны.
Они могут представлять собой характеристики систем, заданные функциональными зависимостями или графиками, уравнениями, описывающими движение систем, автоматами и пр.
Блок принятия решений, блок реализации решений.
В задачах принятия решений по управлению считается, что, на основе модели среды и модели объекта управления, мы можем сформировать множество альтернатив (вариантов воздействия на объект) и для каждой из них определить, насколько данное воздействие ’’приблизит" нас к цели. Справедливость этого предположения во многом зависит от ’’качества" соответствующих моделей.
Основные идеи нечеткого управления
Как видно из приведенного краткого обзора основных понятий теории управления, применение классических методов возможно при наличии модели среды и модели объекта управления. Что делать, если таких моделей нет?
Или модели есть, но для их ’’обсчета" требуются значительные ресурсы? Для ’’модельных" задач последнее может быть не существенным, однако для практических задач большие ресурсы могут быть критичными (например, для систем управления в реальном времени управляющее воздействие должно вырабатываться не более, чем за некоторое время At, иначе решение, пусть самое лучшее, уже никому не нужно; для бортовых систем управления критичным могут быть габариты и вес компьютера: если для работы с моделью требуется супер-ЭВМ, то ее не возьмешь в самолет или автомобиль).
Нечеткие контроллеры как раз и применяются в этих ситуациях. Основная идея заключается в ’’подмене" сложной математической модели реального процесса или объекта на логико-лингвистическую модель управления этим процессом (объектом).
В рамках этого подхода предлагается использовать опыт оператора, управляющего объектом. Стратегия управления, используемого оператором, часто может быть сформулирована как набор правил, которые можно выполнить человеку, но трудно формализовать, используя обычные алгоритмы.
Трудность формализации возникает из-за того, что человек использует качественные понятия (например, ’’давление пара большое", скорость изменения параметра нормальная!', ’’ситуация стабильнал" и т.п.) при описании условий принятия конкретных решений.
При фиксированной цели управления (например, сохранение значения управляемого параметра g в некоторой области допустимых значений G) модель процесса управления может быть выражена в виде множества ’’Если - - - , то ¦ ¦ ¦ " - правил следующим образом.
Пусть состояние управляемого объекта ? описывается набором значений качественных признаков I(?). Множество значений признаков V фиксировано и является конечным (V = {d1, ¦ ¦ ¦ , dm}). Процесс описывается последовательностью состояний
объекта в моменты времени t1,t2, ¦ ¦ ¦ |і(?і:і)i=1 2 . Для достижения цели управления (’’удержания" значения управляемого параметра g в области G в нашем случае) у нас есть возможность изменять значения некоторых управляемых параметров из множества A = {a1, ¦ ¦ ¦ , an}.
Для описания идеи использования нечетких лингвистических регуляторов рассмотрим простейшую ситуацию m = 1,n = 1, то есть ситуацию, когда V = {d}, A = {a}.
Как отмечалось выше, эксперт часто может сформулировать свой опыт управления только для качественных значений d и а. Пусть d = {d1, ¦ ¦ ¦ , ds} и a = {a1, ¦ ¦ ¦ , ar} - набор качественных значений d и a соответственно. Моделью d и a может служить лингвистическая переменная (раздел 4.1) с фиксированным множеством значений или, что то же самое - семантическое пространство (раздел 4.2).
В этом случае d и a - названия соответствующих лингвистических переменных, dl ж aj (i = 1, ¦ ¦ ¦ , s; j = 1, ¦ ¦ ¦ ,r) - ее значения.
Пусть соответствующие нечеткие множества (u) и цаі (v) определены в универсальных множествах U и V соответственно (i = 1, ¦¦¦ , s; j = 1, ¦¦¦ ,r). Тогда правила, которые использует эксперт, можно сформулировать следующим образом: ’’Если d = d\ то a = aj".
Например, ’’Если давление пара очень высокое, то открыть клапан сильно".
Таким образом, моделью объекта управления и среды является их лингвистическое описание; блок принятия решений работает как последовательность ’’Если .. то ..." правил. Однако, как мог заметить внимательный читатель, в приведенной схеме есть некоторое противоречие. Действительно, возникает ситуация, когда элементы одной схемы описываются на разных ’’языках": в среде значения признаков -некоторые числа, отражающие значения физических измеряемых величин, а в модели управления значения признаков - качественные понятия.
Система управления должна взять с объекта управления некоторые числа и выдать на объект опять же некоторые конкретные числа.
Для этого система управления имеет два интерфейса: представления физического значения признака в лингвистическом виде (’’фазификатор") и представления получившегося в результате нечетких рассуждений лингвистического значения управляемого параметра в количественном виде (’’дефазификатор"). Структурная схема нечеткого лингвистического регулятора представлена на рис.
3.2.
В рамках данной общей схемы может быть несколько вариаций. Например, на выходе блока представления количественных значений параметра в виде лингвистической переменной может быть лингвистическое значений с максимальной степенью принадлежности или набор лингвистических значений с указанием степени принадлежности конкретного количественного значения параметра к этим лингвистическим значениям (нечеткое множество типа 2 - раздел 1.1).
Генерация количественного значения на выходе блока представления лингвистического значения в количественном виде может производиться по максимальному значению функции принадлежности, по расположению ’’центра масс" функции принадлежности или другими методами.
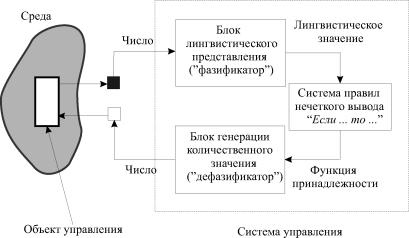
Рис. 3.2:
Различные такие варианты отражены в достаточно большом количестве работ по данному вопросу, опубликованной в рамках проекта FALCON (Fuzzy Algorothms and Logic iu COXtol) в рамках Общеевропейской программы ESPIRIT и представлены практически на всех конференциях по теории нечетких множеств и ее приложениям.
Мы больше не имеем возможности детализировать проблемы приложений методов нечетких рассуждений в управлении. Отметим лишь, что принципы, изложенные в разделах 3.1 3.2 составляют теоретическую базу таких систем.
Заменяя в приведенных в указанных разделах формулах операции max и min на t нормы и t конормы (раздел 3.3) мы получаем набор операторов, которые могут использоваться в нечетких лингвистических регуляторах.
Глава 4 Семантические пространства и их свойства
Понятие лингвистической переменной
Опираясь на понятие нечеткого множества Заде в [17] вводит понятие нечеткой переменной как тройки
{а, U,G),
где а - наименование (имя) нечеткой переменной;
U - область ее определения (универсальное множество);
G - нечеткое множество в U, описывающее ограничения на возможные значения нечеткой переменной а (ее семантику).
В зависимости от характера множества U нечеткие переменные могут быть разделены на числовые и нечисловые. К числовым относятся нечеткие переменные, у которых U С R1.
Дальнейшим шагом является введение понятия лингвистической переменной как пятерки
{A,T (A),U,V,M),
где A - название переменной;
T(A) - терм-множества переменной A, т.е. множество названий лингвистических значений переменной A, причем каждое из таких значений - нечеткая переменная со значениями из универсального множества U;
V - синтаксическое правило (обычно грамматика), порождающее названия значений лингвистической переменной A;
M - семантическое правило, которое ставит в соответствие каждой нечеткой переменной из T(A) нечеткое подмножество универсального множества U.
Пример лингвистической переменной ’’Возраст" представлен на рис. 4.1
Заде различает базовые термины (молодой, среднего возраста, пожилой, ...) и модификаторы (очень, не-, слегка, ...). Модификаторы могут применяться как к базовым терминам (очень молодой, не старый, ... ), так и к комбинациям базового
термина и модификатора (очень-очень старый, слегка не молодой, ...). Правила применения модификаторов задаются синтаксическим правилом V.
Разница между базовыми терминами и модификаторами заключается в следующем. Для базовых терминов функции принадлежности задаются, а модификаторы действуют как некоторые операторы над этими функциями.
Например, в качестве ’’очень" предлагается следующая модификация функции принадлежности термина ’’молодой" [17]: ц (и) = ц2(и). Аналогично ц (и) = ц1/2(и) и т.п. Вопросы адекватности таких преобразований практически не изучались. Одна из причин этого заключается в большой неопределенности операций: для разных ситуаций могут быть разные результаты.
Проблема заключается в том, что для разных контекстов функции принадлежности одного и того же термина могут быть разными. Эта проблема изучается в рамках концепции семантического пространства.
Более подробно с теорией и приложениями лингвистической переменной можно ознакомиться в [17], мы же более подробно остановимся на концепции семантического пространства, его свойствах и приложениях.
Полные ортогональные семантические пространства (ПОСП)
Рассмотрим ситуацию, когда лингвистическая переменная A = ’’РОСТ" имеет два терм - множества Ti(A) = {низкий, высокий} и T2(A) = {низкий, средний , высокий}.
Интуитивно ясно, что функции принадлежности понятий ’’низкий" и ’’высокий" в первом и во втором случае будут различаться: новое понятие ’’средний" модифицирует их, сдвигает к концам универсума (Рис. 4.2)
Последнее говорит о том, что семантика некоторого термина зависит от контекста, или набора значений соответствующей лингвистической переменной. Таким образом,
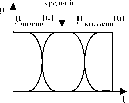
Рис. 4.2:
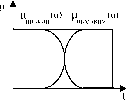
функция принадлежности любого термина без указания контекста, вообще говоря, не имеет смысла.
Будем называть семантическим пространством лингвистическую переменную с фиксированным терм-множеством, т.е. четверку
5 = {A,T (A),U,M).
Иными словами, семантическое пространство - это набор нечетких переменных
S = {ai,U,Gi),..., {an,U,Gn). (4-1)
При этом для одного и того же имени A могут существовать различные пространства
Si = {A, T1(A),U,M1),...,Sk = {A, Tk (A), U, Mk).
Можно ли как-то сравнивать семантические пространства, выбирать наилучшее в некотором смысле ? Рассмотрим следующий пример.
Пример 19 Рассмотрим процесс описания человеком, некоторых реальных объектов на примере описания других людей. Описывая ВОЗРАСТ человека, мы можем использовать несколько вариантов множества значений признака ’’ВОЗРАСТ":
- T1 = {молодой, старый };
- Т2 = {молодой, среднего возраста, старый };
- Tn = {юный, очень молодой, ..., очень старый }.
Какое из этих множеств лучше с точки зрения ’’легкости" описания возраста?
Множество T1 не является таковым, так как существует много людей, для которых обозначения одинаково не подходят. Мы, испытываем, трудности описания, из-за, недостатка значений.
Множество Tn также является, ’’плохим," из-за, того, что для, одного и того же реального объекта, могут оказаться, одинаково подходящим,и несколько значений признака.
Данный пример позволяет нам сформулировать следующую проблему выбора оптимального множества значений качественных признаков.
Проблема 1. Можно ли, учитывая некоторые особенности восприятия человеком, объектов реального мира и их описания, сформулировать правило вы,бора оптимального множества значений признаков, по которым описываются эти объекты? Возможны два критерия оптимальности:
Критерий 1. Под оптимальными понимаются такие множества значений, используя которых человек испытывает минимальную неопределенность при описании объектов.
Критерий 2. Если объект опись/,вается некоторым количеством экспертов, то дующим двум требованиям:
(4) полнота: Уu Е U 3j (1 j t) : pj (u) = 0;
t
(5) ортогональность: Уи Е U Pj (u) = 1.
j=i
Эти ограничения также являются довольно естественными. Требование (4) означает, что для каждого объекта найдется хотя бы одно понятие, его описывающее с ненулевой степенью; (5) означает достаточную разделимость понятий, образующих семантическое пространство, отсутствие синонимии или семантически близких терминов.
Будем обозначать через Gt (L) множество из t функций из L, удовлетворяющих требованиям (4), (5).
Семантические пространства, функции принадлежности понятий которых принадлежат Gt(L), будем называть полными ортогональными семантическими пространствами (ПОСП).
В рамках ПОСП можно ввести понятие степени нечеткости или меры внутренней неопределенности, которое позволяет выбирать наилучшие пространства для описания человеком реальных объектов (см. пример 19).
Степень нечеткости ПОСП
Прежде всего заметим, что определенное в 4.2 множество L функций является подмножеством множества S2 интегрируемых на отрезке функций, поэтому мы можем ввести метрику на L, например,
P(f,9)= \f(и) - 9(u)\du, f Е L, g Е L.
Ju
Мы также можем ввести метрику в Gt(L).
Лемма 1 Пусть st Е Gt(L), s't Е Gt(L),
St = {yi(u),i2u(),---,ItXu)}, s't = {y,1(u),y,2(u),- ¦ ¦,lt(u)}, p(f, g) - некоторая метрика в L.
Тогда
t
d(st,st) = Y. p(ij ’ij) (4-2)
j=i
есть метрика в Gt(L).
Доказательство. Для доказательства леммы необходимо проверить выполнение аксиом расстояния (с.
19).
Так как p(pj, pj) - метрика, то выполнение первых двух аксиом для ( 4.2) очевидно. Проверим выполнение аксиом 3, 4.
3. d(sf st) = 0 yj(1 j t) P(Pj’Pj) = 0
yj (1 j t) Pj = Pj st = s't¦
YtP(Ij,lj) + E P(lj,l'j) = d(St,s1) + d(s't,s't).
4. d(st,s't) = E P(Ij,lj) E [p(!j,l'f) + P(lj,Vj)]
j=i
j=i
j=1
j=1
Лемма доказана.
Для формулировки аксиом необходимо определить совокупность множеств, базирующуюся на данной совокупности нечетких множеств и являющихся ’’четкими". Это множество характеристических функций, определяемых следующим образом.
Пусть st G Gt (L) определена на U и включает функции принадлежности ц1 (u), i2(u),yt(u). Построим совокупность характеристичес ких функций st, состоящую из функций h1 (u), h2(u),..., ht(u), где
1, если max1jt fij (u) = yi(u) 0, в противном случае
hi(u) =
(4.3)
Будем называть st ближайшей совокупностью характеристических функций для
st G Gt(L)-
Под степенью нечеткости st G Gt(L) будем понимать значение функционала ?(st), определенного на множестве функций принадлежности st и удовлетворяющего следующим аксиомам:
A1. 0 ? (st) 1 Vst G Gt(L).
A2. ?(st) = 0 ^ yu G U 3j(1 j t) :
ij(u) = 1, Hi(u) = 0 Уі = j.
A3. ?(st) = 1 yu G U 3i1,i2(1 i1,i2 t) :
Ti1 (u') цІ2 (u) lmax1jt Tj (u') -
A4. Пусть st и s't, определены на универсальных множествах U и U' соответственно; t и t' могут быть равны или не равны друг другу. Тогда
? (st) ? (st,), если p(st, st) p(s't,, st, '), где p(.,.) - некоторая метр ика в Gt(L).
Аксиома A1 определяет границы изменения степени нечеткости.
Аксиомы A2 и A3 описывают совокупности нечетких множеств, на которых ?(st) достигает максимальные и минимальные значения, то есть максимально ’’четкие" и максимально ’’нечеткие" совокупности нечетких множеств соответственно.
Аксиома A4 определяет для каждой пары совокупностей нечетких множеств правило сравнения степени их нечеткости. Ее можно интерпретировать следующим образом: чем ближе некоторая совокупность нечетких множеств к своей ближайшей совокупности характеристических функций, тем меньше степень ее нечеткости.
Существуют ли функционалы, удовлетворяющие сформулированным аксиомам? Ответ на этот вопрос дает следующая
Теорема 4 (Теорема существования). Пусть st G Gt(L). Тогда функционал
где
lq (и) = max щ (и), у* (и)= max щ {и), (4.5)
1 13t 13t; j=i*
f удовлетворяет следующим требованиям:
F1: f (0) = 1, f (1)=0;
F 2 : f убывает,
- является степенью нечеткости st, то есть удовлетворяет аксиомам A1 A4.
Доказательство 1. Выполнение аксиомы A1 очевидно.
2. Обозначим через y(st,u) подынтегральную функцию в ( 4.4) В этом случае:
?(st) = 0 Уи Е U n(st, и) = 0
Уи Е U щ* (и) Ці* (и) = 1
Уи Е U3j(1 j t) : /ij(и) = 1, щі(и) = 0 Уі = j.
3. Аналогично пункту 2,
?(st) = 1 Уи Е U n(st, и) = 1
Уи Е U щ* (и) у* (и) = 0
Уи Е U Зіі, і2(1 іі,і2 t) :
Уіц (и) Уі2 (и) max1jt Pj (и') .
4. Рассмотрим произвольные st, s[, Е Gt(L).
?(st) ?(st’) ^ Іиi f (lq(и?) lq (и1))ди1 ф\ Іи2 f (l\(и2) (и2))Ли2
Лиц Іиi (lq(и1) iq (и1))ди1
Т2(..2 V
\U2\
- \и2\
В данных преобразованиях вторая эквивалентность является следствием определения функции ^требование F 2), третья эквивалентность - следствие неравенства 0 уі * (и) щ * (и) 1 У и Е U, замен а 1 и 0 на he соответствующими индексами
(последняя эквивалентность) - следствие определений h ( 4.3) и pi*i (u), (u) ( 4.5).
Последнее неравенство мы можем переписать следующим образом.
где d(h,p) = Jv \h(u) p(u)\du мера в L.
Последнее неравенство есть расстояние между st и st (Лемма 1).
Итак, при выполнении условий теоремы существует мера, для которой С(st) С(4), если p(st, gt) p(s't,,sg).
Теорема существования полностью доказана.
Достаточно очевидно, что существует только одна линейная функция, удовлетворяющая F1, F 2. Это функция
f (x) = 1 x.
Можно также описать подмножество полиномов второй степени, удовлетворяющих F1, F2. Это параметрическое семейство функций
.2
fa(x) = ax2 (1 + a)x + 1.
Подмножества функций других типов (логарифмических, тригонометрических и др.), удовлетворяющих F1, F2 могут быть описаны аналогичным образом. Подставляя эти функции в формулу ( 4.4), мы получаем функционалы, удовлетворяющие A1 A4, то есть степени нечеткости.
Какие из этих классов функционалов ’’лучше"? Это довольно сложный вопрос, ответ на который зависит от конкретного приложения. Мы не будем углубляться в конкретные проблемы, а изучим некоторые общие свойства простейшего из таких функционалов - функционала из класса линейных функций f.
Некоторые свойства степени нечеткости ПО СП
Мы приведем свойства степени нечеткости для линейной функции f:
где (u), (u) описываются ( 4.5).
Функционал С(st) может быть интерпретирован как средняя степень трудностей описания человеком реальных объектов (ситуаций) в рамках соответствующего семантического пространства.