Обучение искусственных нейронных сетей
В общем случае, любой сигнал может быть описан вектором X = {.у. : і = 0...(/7 -1)}, п - число нейронов в сети и размерность входных и выходных векторов. Каждый элемент у равен либо +1, либо -1. Обозначим вектор, описывающий к -й образец, через Хк , а его компоненты, соответственно, - уА, к = 0...(ш -1), т - число образцов. Когда сеть распознает (или вспомнит) какой-либо образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = Хк, где Y -вектор выходных значений сети: Y = (у. : / = 0,...(л -1)}.
В противном случае, выходной вектор не совпадет ни с одним образцовым.
На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом [32]:
{/-1
V k * . , -
/ X: X I Ф )
h,J ¦ о, / = j
Здесь i и j ^ индексы, соответственно, прсдсинаптического и постси-
к к ¦ ~ . - ,
наптического нейронов; .т, , х. - и и у-и элементы вектора к-то
образца.
Алгоритм функционирования сети следующий ( р - номер итерации):
1. На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений аксонов:
уДО) - хп і = 0...(я -1), (1.12)
поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от у. означает нулевую итерацию в цикле работы сети.
2. Рассчитывается новое состояние нейронов
¦?/(/? + !) = Хиух.(р), у = 0...(/7-1) (1.13)
/=о
и новые значения аксонов
y/(/? + l) = /[5/(7? + l)j, (1.14)
где/- активационная функция в виде скачка, приведенная на рис. 1.8а.
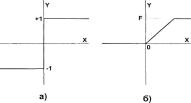
Рис. 1.8 Активационные функции
3. Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да - переход к пункту 2, иначе (если выходы застабили-зировались) - конец.
При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.
Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов т не должно превышать значения равного 0.15-п . Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот. Еще одним недостатком сетей Хопфилда является их тенденция стабилизироваться в локальном, а не в глобальном минимуме.
Эта трудность преодолевается в основном с помощью класса сетей, известных под названием машин Больцмана, в которых изменения состояний нейронов обусловлены статистическими, а не детерминированными закономерностями [32]. Принцип машины Больцмана может быть перенесен на сети практически любой конфигурации, хотя устойчивость не гарантируется.
Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры (рис.
1.9).
Сеть состоит из двух слоев. Первый и второй слои имеют по т нейронов, где т - число образцов.
Нейроны первого слоя имеют по п синапсов, соединенных с входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями.
Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.
Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах.
Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.
На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:
Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 е J/ . Синапс нейрона, связанный с его же аксоном имеет вес +1.
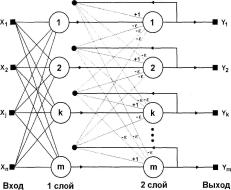
Рис. 1.9. Структурная схема сети Хэмминга
Алгоритм функционирования сети Хэмминга следующий:
1. На входы сети подается неизвестный вектор Х= {.т, : і = 0...(н-1)} ,
исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):
У)?) =ЯГ = 'YjW4X^Tj - ./ = 0...(т -1). (1.17)
і=0
После этого полученными значениями инициализируются значения аксонов второго слоя:
у}2)=У/\ 7 = 0...(т-1). (1.18)
2. Вычисляются новые состояния нейронов второго слоя:
т 1
Sj(2)(p + ^) = yj(p)-e^yk{2)(p), к * j, j = 0...(т -1) (1.19)
А=0
и значения их аксонов:
X/(2)(/? + l) = /[^'(2)(P + 1)J 7=0.. .(ли 1). (1.20)
Активационная функция / имеет вид порога (рис. 1.86), причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.
3. Проверка, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да - перейди к шагу 2. Иначе - конец.
Из алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).
Обсуждение НС с обратными связями, реализующих ассоциативную память, было бы неполным без хотя бы краткого упоминания о двунаправленной ассоциативной памяти (ДАП). Она является логичным развитием парадигмы сети Хопфилда, к которой для этого достаточно добавить второй слой.
Структура ДАП представлена на рис. 1.10.
обратная связь
Как и сеть Хопфилда, ДАП способна к обобщению, вырабатывая правильные реакции, несмотря на искаженные входы. Кроме того, могут быть реализованы адаптивные версии ДАП, выделяющие эталонный образ из зашумленных экземпляров.
Эти возможности сильно напоминают процесс мышления человека и позволяют искусственным НС сделать шаг в направлении моделирования мозга.
Сеть способна запоминать пары ассоциированных друг с другом образов. Пусть пары образов записываются в виде векторов
Хк = (х/ : г = 0...(/г-1)} и Yk = {у/ : j = 0...(m-l)}, к = 0...(г-1), где г - число пар. Подача на вход первого слоя некоторого вектора Р= {/?, : і = 0...(и-1)} вызывает образование на входе второго слоя некоего другого вектора Q= {qf : j = 0...(/и-1)}, который затем снова поступает на вход первого слоя..
При каждом таком цикле, вектора на выходах обоих слоев приближаются к паре образцовых векторов, первый из которых - X - наиболее походит на Р, который был подан на вход сети в самом начале, а второй - Y - ассоциирован с ним. Ассоциации между векторами кодируются в весовой матрице W(l) первого слоя.
Весовая матрица второго слоя \?2) равна транспонированной первой (\?(1) )т. Процесс обучения, так же как и в случае сети Хопфилда, заключается в предварительном расчете элементов матрицы W (и соответственно W1 ) по формуле
і' = 0...(л-1), j - 0...(m -1). (1.21)
к
Эта формула является развернутой записью матричного уравнения W = ?xT\ (1.22)
к
для частного случая, когда образы записаны в виде векторов, при этом произведение двух матриц размером соответственно [лхі] и [Іхш ] приводит к (1.21).
Как и сети Хопфилда, ДАП имеет ограничения на максимальное количество ассоциаций, которые она может точно воспроизвести. Если этот лимит превышен, сеть может выработать неверный выходной сигнал, воспроизводя ассоциации, которым не обучена.
В работе [70] приведены оценки, в соответствии с которыми количество запоминаемых ассоциаций не может превышать количества нейронов в меньшем слое. При этом предполагается, что емкость памяти максимизирована посредством специального кодирования, при котором количество компонент со значениями + 1 равно числу компонент со значениями -1 в каждом биполярном векторе.
Более точные оценки могут быть получены в результате обобщения работы [70] по оценке емкости сетей Хопфилда.
Несмотря на эти проблемы, ДАП является объектом интенсивных исследований. Основная привлекательность ДАП, как и сетей Хопфилда и Хэмминга, заключается в их простоте.
Легкость построения программных и аппаратных моделей делает эти сети привлекательными для многих применений.
Еще одной разновидностью искусственных НС с обратными связями являются самоорганизующиеся карты Кохонена (SOM) [82]. Такая сеть является специальным случаем сети обучающейся методом соревнования и представляет собой векторный квантователь, задачей которого является
определение принадлежности входного вектора X = {x{,x2,...,xN}T к одному из А/ возможных кластеров, представленных векторными центрами \? = {Wn,wj2,...,wjN}T (j = 1, 2,...,М). Считается, что вектор X принадлежит к j -му кластеру, если расстояние d}, определяемое как
у=2,-'Д2. с-23)
/=і
для / -го центра кластера W минимально, то есть если йГ. dk для каждого к Ф j [6]. Если узлы квантователя являются линейными, а вес і -го входа / -го узла равен ??(/ для каждого і и /, то очевидно, что при соответствующих значениях порогов каждый і -й выход сети с точностью до несущественных постоянных будет равен евклидову расстоянию d. между предъявленным входным вектором X и / -м центром кластера.
При обучении НС квантователя предъявляются входные векторы без указания желаемых выходов и корректируются веса согласно алгоритму, предложенному Т. Кохоненым (будет рассмотрен в п.1.3.2).
Самоорганизующиеся карты Кохонена могут быть использованы для проектирования многомерных данных, аппроксимации плотности и кластеризации. Эти сети успешно применяются для распознавания речи, обработки изображений, в робототехнике и в задачах управления [6, 14, 19].
Обучение искусственных нейронных сетей
1.3.1. Обучение с учителем
Когда идет разговор об использовании НС и нейросстевых алгоритмов, почти всегда подразумеваются определенные процедуры их обучения. НС представляет собой адаптивную систему, жизненный цикл которой состоит из двух независимых фаз - обучения и работы сети.
Обучение считается законченным, когда сеть правильно выполняет преобразование на тестовых примерах и дальнейшее обучение не вызывает значительного изменения настраиваемых весовых коэффициентов. Далее сеть выполняет пре-ооразование ранее неизвестных ей данных на основе сформированной ею
в процессе обучения нелинейной модели процесса. Сеть успешно работает до тех пор, пока существенно не изменится реальная модель отображаемого явления (например, в случае возникновения ситуации, информация о которой никогда ни предъявлялась сети при обучении). После этого сеть может быть дообучена с учетом новой информации, причем при дообучении предыдущая информация не теряется, а обобщается с вновь поступившей.
При повреждении части весовых коэффициентов НС ее свойства могут быть полностью восстановлены в процессе дообучения.
От того, насколько качественно будет выполнен этап обучения НС, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. Теория обучения рассматривает три фундаментальных свойства, связанных с обучением по примерам: емкость, сложность образцов и вычислительная сложность. Под емкостью понимается, сколько образцов может запомнить сеть и какие функции и границы принятия решений могут быть на ней сформированы. Сложность образцов определяет число обучающих примеров, необходимых для достижения способности сети к обобщению.
Важной характеристикой является время затрачиваемое на обучение. Как правило, время обучения и качество обучения связаны обратной зависимостью и выбирать эти параметры приходится на основе компромиса.
Существуют три парадигмы обучения: с учителем, без учителя (самообучение) и смешанная.
В свою очередь множество различных алгоритмов обучения делятся на два больших класса: детерминистских и стохастических алгоритмов. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором - она производится на основе действий, подчиняющихся некоторому случайному процессу.
Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, представляющий собой требуемый выход. Вместе они называются обучающей парой.
Обычно сеть обучается на некотором числе таких обучающих пар.
Когда в сети только один слой, алгоритм ее обучения с учителем довольно очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети.
В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двух или более слойную НС уже невозможно обучить, руководствуясь только величинами ошибок на выходах этой сети. Один из вариантов решения этой проблемы - разработка наборов выходных сигналов, соответствующих входным, для каждого слоя НС, что, конечно, является очень трудоемкой операцией и не всегда осуществимо. Второй вариант - динамическая под-24
стройка весовых коэффициентов синапсов, в ходе которой выбираются, как правило, наиболее слабые связи, которые изменяются на малую величину в ту или иную сторону. Сохраняются же только те изменения, которые повлекли уменьшение ошибки на выходе всей сети. Очевидно, что данный метод проб, несмотря на свою кажущуюся простоту, требует громоздких рутинных вычислений. И, наконец, третий, более приемлемый вариант - распространение сигналов ошибки от выходов НС к ее входам, в направлении обратном прямому распространению сигналов в обычном режиме работы.
Этот алгоритм обучения НС получил название процедуры обратного распространения (back-propagation algorithm) и является наиболее широко используемым. Именно он будет более подробно рассмотрен в дальнейшем.
Согласно методу наименьших квадратов, минимизируемой целевой функцией ошибки НС является величина:
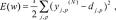
где y(jNp - реальное выходное состояние нейрона j выходного слоя N
нейронной сети при подаче на ее входы р -го образа; d - - идеальное
(желаемое) выходное состояние этого нейрона.
Суммирование ведется по всем нейронам выходного слоя и по всем обрабатываемым сетью образам. Минимизация ведется методом градиентного спуска, что означает подстройку весовых коэффициентов следующим образом:
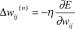
Здесь Wj- - весовой коэффициент синаптической связи, соединяющей і -й нейрон слоя (п -1) с у -м нейроном слоя п , р - коэффициент скорости обучения, 0 Tj 1.
Как показано в [100]:
(1.26)
дЕ _ дЕ dy’j dsj
дУ .і ds- 4
Здесь под у j, как и раньше, подразумевается выход нейрона j , а под Sj ~ взвешенная сумма его входных сигналов, то есть аргумент активацион-
Э? /
ной функции. Множитель ' V^s является производной этой функции по
ее аргументу. Из этого следует, что производная активационной функция Должна быть определена на всей оси абсцисс. В связи с этим функция единичного скачка и прочие активационные функции с неоднородностями не подходят для рассматриваемых НС.
В них применяются такие гладкие функции, как гиперболический тангенс или классический сигмоид с экспонентой. В случае гиперболического тангенса
^ = \-s2 : (1.27)
Эх
Третий множитель , очевидно, равен выходу нейрона преды
дущего слоя ?/~ -
Что касается первого множителя в (1.26), он легко раскладывается следующим образом [100]:
_ у дЕ дук dsк _ у дЕ Эук (Н+і)
(1.28)
дЕ
(1.29)
Здесь суммирование по к выполняется среди нейронов слоя (п + 1). Введя новую переменную s о.) _ дЕ Е 1 ду. Эх,
мы получим рекурсивную формулу для расчетов величин 8 слоя п из величин 5а('н1) более старшего слоя (л + 1).
El.
ds,
Is
(И+1) (И+І)
wJk
(я)
(1.30)
Для выходного же слоя
5.я'=(?,'')-/.)- (1.3D
Теперь можно записать (1.25) в раскрытом виде:
ДиЛ’ =-ri-SJMy,{-'). (1.32)
Иногда для придания процессу коррекции весов некоторой инерционности, сглаживающей резкие скачки при перемещении по поверхности целевой функции, (1.32) дополняется значением изменения веса на предыдущей итерации
Aw,(V) = -rKMw/'V -1) + (1 - И)5 /VЯ_1)) ’ 0.33)
где /л - коэффициент инерционности, t - номер текущей итерации.
Таким образом, полный алгоритм обучения НС с помощью процедуры обратного распространения строится в следующем порядке [100]:
1. Подать на входы сети один из возможных образов и в режиме обычного функционирования НС, когда сигналы распространяются от входов к выходам, рассчитать значения последних. Как было отмечено ранее м
sr = lyr
v(w)
(1.34)
/=о
где М - число нейронов в слое (л-1) с учетом нейрона с постоянным выходным состоянием +1, задающего смещение; у/ п = хУп - і -й вход
нейрона j слоя п .
(1.35)
(1.36)
где /() - сигмоид, у (0) = / ,
х Я 1 ’
где Iq - q-я компонента вектора входного образа.
2. Рассчитать 51Л ) для выходного слоя по формуле (1.31).
Рассчитать по формуле (1.32) или (1.33) изменения весов Д??іЛ) слоя
N.
3. Рассчитать по формулам (1.30) и (1.32) (или (1.30) и (1.33)) соответственно 8(п) и Дw(n) для всех остальных слоев, п = N - 1,...,1.
4. Скорректировать все веса в НС
= + (1.37)
5. Если ошибка сети существенна, перейти на шаг 1. В противном случае - конец.
На шаге 1, на входы сети попеременно в случайном порядке предъявляются все тренировочные образы, чтобы сеть, образно говоря, не забывала одни по мере запоминания других. Рассмотренный алгоритм иллюстрируется рис.
1.11.
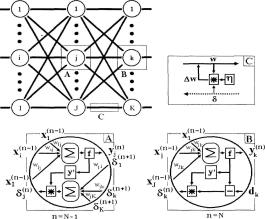
Рис. 1.11. Диаграмма сигналов в сети при обучении по алгоритму обратного распространения
Из выражения (1.32) следует, что, когда выходное значение у-" !) стремится к нулю, эффективность обучения заметно снижается. При двоичных входных векторах в среднем половина весовых коэффициентов не будет корректироваться [110], поэтому область возможных значений выходов нейронов [0,1] желательно сдвинуть в пределы [-0.5, +0.5], что достигается простыми модификациями логистических функций. Например, сигмоид с экспонентой преобразуется к виду
/¦(л) = -0.5 +----- (1-38)
\+е-са
Рассматриваемый алгоритм обучения НС имеет несколько узких мест. Во-первых, в процессе обучения может возникнуть ситуация, когда большие положительные или отрицательные значения весовых коэффициентов сместят рабочую точку на сигмоидах многих нейронов в область насыщения.
Малые величины производной от логистической функции приведут в соответствие с (1.30) и (1.31) к остановке обучения, что парализует НС. Во-вторых, применение метода градиентного спуска не гаран-28
тирует, что будет найден глобальный, а нс локальный минимум целевой функции. Эта проблема связана еще с одной, а именно - с выбором величины скорости обучения.
Доказательство сходимости обучения в процессе обратного распространения основано на вычислении производных, то есть приращении весов и, следовательно, скорость обучения должна быть бесконечно малой, однако в этом случае обучение будет происходить неприемлемо медленно. С другой стороны, слишком большие коррекции весов могут привести к постоянной неустойчивости процесса обучения.
Поэтому в качестве V) обычно выбирается число меньше 1, но не очень маленькое, например 0.1, и оно, в общем случае, может постепенно уменьшаться в процессе обучения. Кроме того, для исключения случайных попаданий в локальные минимумы иногда, после того как значения весовых коэффициентов застабилизируются, г] кратковременно сильно увеличивают, чтобы
начать градиентный спуск из новой точки. Если повторение этой процедуры несколько раз приведет алгоритм в одно и то же состояние НС, можно более или менее уверенно сказать, что найден глобальный минимум.
Алгоритмы модифицирующие процедуру обратного распространения, изменяющие процедуру выбора оптимизируемой функции критерия, выбор оптимального шага и правила коррекции параметров обучаемой сети подробно описаны в [53, 75].
Отметим, что все эти алгоритмы не согласуются с данными нейробио-логии, где показано, что сигналы в биологических нейронных сетях могут распространятся только в одном, прямом направлении.
В работе [1] предложены алгоритмы настройки многослойной НС без использования процедуры обратного распространения ошибки, которые получили название "автономные алгоритмы". Эти алгоритмы основаны на том факте, что для многослойной НС существует некоторое множество значений настраиваемых параметров, на котором вектор коррекции настраиваемых параметров вычисляется достаточно просто.
Эти алгоритмы при прочих равных условиях хуже решают задачу обучения, чем алгоритмы обратного распространения ошибки, однако они являются структурно независимыми и очень простыми с вычислительной точки зрения.
Обучение без учителя
Обучение без учителя является более правдоподобной моделью обучения в биологической системе. Процесс обучения, как и в случае обучения с учителем, заключается в подстраивании весов синапсов. Некоторые алгоритмы предусматривают изменение и структуры сети, то есть количество нейронов и их взаимосвязи, но такие преобразования правильнее назвать более широким термином - самоорганизацией.
Очевидно, что подстройка синапсов может проводиться только на основании информации, доступной нейрону, то есть его состояния и уже имеющихся весовых коэффициентов. Исходя из этого соображения и, что более важно, по аналогии с известными принципами самоорганизации нервных клеток, построены алгоритмы обучения Хебба [32].
Сигнальный метод обучения Хебба заключается в изменении весов по следующему правилу:
% (0 = ??.. (t -1) + qy,.(~‘V/(,,), (1.39) где у/{п м - выходное значение / -го нейрона (/?-])-го слоя, у .п) - выходное значение у-го нейрона слоя п; ??;/(у) и ??у (/-1) - весовой коэффициент синапса, соединяющего эти нейроны, на итерациях / и /-1 соответственно; а- коэффициент скорости обучения. Здесь и далее для общности под п подразумевается произвольный слой сети.
При обучении по данному методу усиливаются связи между возбужденными нейронами.
Существует также и дифференциальный метод обучения Хебба.
wM) = и,„0-1) + а-[)?-(0-Л,-|,(-1)[к,,(0-.?;',((-1)]. (1.40)
Здесь у/ п(/) и у/п ^(/-І) - выходное значение і -го нейрона (я-І)-го слоя соответственно на итерациях ( и /-1; yf(n\t) и у(,,)(/-1) - тоже самое для у-го нейрона слоя п . Как видно из формулы (1.40), сильнее всего обучаются синапсы, соединяющие те нейроны, выходы которых наиболее динамично изменились в сторону увеличения.
Полный алгоритм обучения в соответствии с методом Хебба может быть представлен в следующем виде:
Шаг 1. На стадии инициализации всем весовым коэффициентам присваиваются небольшие случайные значения.
Шаг 2. На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических прямопоточных (feedforward) сетей, то есть для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная (передаточная) функция нейрона, в результате чего получается его выходное значение у,1'0, / = 0...(М, -1), где М - число нейронов в слое /; п = 0...(Af -1), а N - число слоев в сети.
Щаг 3. На основании полученных выходных значений нейронов по формуле (1-39) или (1-40) производится изменение весовых коэффициентов.
Шаг 4. Если выходные значения сети не стабилизируются с заданной точностью, то осуществляется повторение цикла, начиная с шага 2. Применение этого нового способа определения завершения обучения, отличного от использовавшегося для сети обратного распространения, обусловлено тем, что подстраиваемые значения синапсов фактически не ограничены.
На втором шаге цикла попеременно предъявляются все образы из входного набора.
Следует отметить, что вид откликов на каждый класс входных образов не известен заранее и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации.