Винтина П. - Модель поведения цены SABR

Московский Государственный Университет им.М.В.Ломоносова

Введение

Обычно европейские опционы оценивают и хеджируют, используя для этого модель Блэка или , что то же самое, Блэка-Шоулза. Модель Блэка устанавливает однозначное соотношение между ценой европейского опциона и параметром волатильности. Таким образом опционы часто оценивают используя подразумеваемую волатильность (implied volatility) ay - уникальное значение волатильности, подставляя которое в формулу Блэка - Шоулза, получаем правильную цену опциона. В теории волатильность ay в формуле Блэка - Шоулза является константой.

На практике опционы с разными страйками K требуют использования различных значений ay для того, чтобы соответствовать своим рыночным ценам. Управление этими улыбками воолатильности корректно является очень важным для для fixed income и foreign exchange десков, ибо обычно на этих десках бывают огромные позы со всевозможными страйками. Ну и понятно, что использование разных волатильностей для разных опционов делает очень сложным успешное управление рисками по модели Блэка - Шоулза. Развитие моделей локальной волатильности Dupire и Derman-Kani было очень большим шагом в управлении улыбками волатильности.

Эти модели можно откалибровать так, чтобы они удовлетворяли рыночным ценам. В настоящее время эти модели являются наиболее популярным способом управления риском, вызванным улыбками волатильности ( дальше - smile risk). Однако, как мы поймем далее, динамика поведения улыбок волатильности, предсказанная этими моделями, является прямо противоположной динамики, которую мы наблюдаем на рынке.

Для разрешения этой проблемы мы разберем модель SABR, модель случайной волатильности, в которой цена актива и волатильность коррелируют между собой.

Начальные сведения

Рассмотрим европейский колл на актив с датой исполнения t_ex , датой поставки t_set и страйком K. Если держатель опциона испол-
няет его во время t_ex , то он получает актив и платит страйк K во время t_set. Для того, чтобы вывести цену опциона, определим F (t) -форвардная цена актива на форвардный контракт, исполняющийся во время t_set, а также определим f = F(О)-сегодняшнюю форварную цену.

Также пусть D(t) будет коеффициентом дисконтирования, т.е. пусть D(t) равен стоимости сегодня $1, с рассчетами на дату t. Теория мартингалов позволяет получить, что при обычных условиях, есть мера, известная как форвардная мера, по которой, стоимость европейского опциона может быть получена как мат. ожидание выплаты. Таким образом цена европейского колла равна
Vcall = D(tset)E { [F(e) - K]+ |Fo} (1)
а цена соответствующего пута равна
Vput = D(tsetE {[K F (tex)+\Fo} = Vcall + D(tset)[F f ] (2)
(подробный вывод этих формул можно найти в [1]) Здесь мат. ожидание берется по форвардной мере, а условие ^₀надо понимать как при наличии всей доступной информации в момент времени t = О. Теория мартингалов также показывает, что форвардная цена F(t) является мартингалом по данной мере а также то, что F(t) подчиняется закону: dF = C(t, *)dW , F(0) = f для некоторого коэффициента C(t, *), где dW является броуновским движением относительно данной меры. Коэффициент C(t, *) может быть постоянным или случайным и может зависеть от любой информации, которая может быть получена во время t. Это получено из теории безарбитражного ценообразования. На самом-то деле нельзя определить этот коэффициент на чисто теоретических основах.

Вместо этого предлагается построить его математическую модель.

Модель Блэка и implied volatility

Для того, чтобы двигаться дальше необходимо составить модель для коэффициента C(t, *). Блэк предлагал C(t, *) брать равным авF(t), где волатильность ав является константой. Тогда форвард-
ная цена F(t) подчиняется геометрическому броуновскому движению:
dF арF(t)dW, F(0) = f
Оценивая формулы (1), (2), согласно данной модели, получаем формулу Блэка:
Vcall D(tset){fN(di) - KN(d2)}
Vput Vcall + D(tset)[K f ]
, где
l9 K ± 2 авtex di,2 -/ -
а tex
для цены всех европейских коллов и путов, что хорошо известно из фундаментальной теории. Все параметры в формуле Блэка легко наблюдаемы, за исключением волатильности ар- Накопленная волатильность для опциона (implied volatility)-это значение ар , которое надо использовать в формуле Блэка для получения верных рыночных цен опционов.

Т.к. цены коллов и путов являются растущими функциями ар, сама implied volatility единственна. На самом деле на некоторых рынках стандартной практикой является котировать опционы в терминах implied volatility.
Вывод формулы Блэка подразумевает, что волатильность ар является константой для каждого актива A. Однако, implied volatility, необходимая для соответствия теоретических цен опционов их рыночным ценам, почти всегда варьируется при изменении как страйка, так и времени исполнения (см. Рисунок 1).

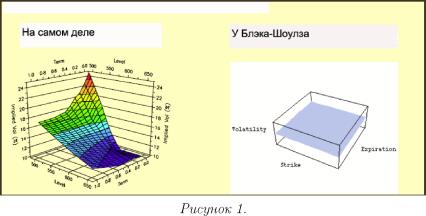
Изменение волатильности ар означает использования уже другой модели для б.а. для каждого K и t_ex. Это является причиной нескольких проблем, касающихся управления большими стелажами опционов.
Первая проблема - оценка всяческой экзотики. Допустим, надо оценить колл с двумя страйками.

В таком случае непонятно для какого страйка считать implied volatility. Вторая проблема - хеджирование.

Раз уж разные модели используются для различных страйков, то непонятно, будут ли риски, посчитанные для одного страйка соответствовать тем же рискам, но посчитанным для другого страйка.

Модель локальной волатильности

Фундаментальное решение данной проблемы представлено моделями локальной волатильности, например моделью Dupire (более подробно в [3] и [4]). Он предлагал положить dF = ai_oc(t,F)FdW , F(0) = f. Dupire говорил, что вместо построения теорий по поводу неизвестной волатильности, нужно просто подбирать ее исходя из рынка, калибруямодель локальной волатильности к рыночным ценам европейских опционов.

Но у данной модели есть один очевидный недостаток - модель предсказывает, что рыночная улыб-кабудет двигаться в направлении, противоположном направлению движения цены б.а., что на практике совсем не так.

Модель SABR

Несостоятельность модели локальной волатильности означает, что мы не можем использовать марковскую модель, основанную на одном единственном броуновском движении для управления риском. Вместо того, чтобы строить немарковскую модель или основывать ее на неброуновском движении, предлагается использовать двухфакторную модель. Для выбора второго параметра заметим, что на большинстве рынков наблюдаются как относительно тихие, так и бурныепериоды в движении цен.

Это наводит на мысль, что волатильность не является константой, а сама является случайной функцией времени. Таким образом мы выбираем неизвестный коэффициент C(t, *) равным aFe, где волатильность а сама является случайным процессом.

Выбирая простейший процесс для а, получаем стохастическую-а^р модельа.к.а. SABR.
В данной модели форвардная цена и волатильность определяются так:
dF = a Fв dWi, F (0) = f
da = ?а dW₂, а(0) = а
,где два процесса связаны соотношением:
dW_idW₂ = pdt
Было также предложено и много других стохастических моделей, но SABR оказался простейшей и наиболее популярной моделью. SABR можно использовать для точного соответствия кривым implied volatility, наблюдаемым на рынке для любой отдельной t_ex. И что более важно, эта модель предсказывает верную динамику кривых implied volatility.

Все это делает модель SABR очень эффективным средством управления риском implied volatility на рынке, где у каждого б.а. существует единственная дата исполнения. Выпишем результаты оценки европейских путов и коллов согласно модели SABR:
Vcall = D(t„t){fN(d_l) - KN(d2)}
Vput = Vcall + D{t_set)\K f ]
dl,2 =
log K ± 1 ape
implied volatility ay{f,K) удовлетворяет:
в {f,K ) =
{fk)(1e)/2{1 + logK + if4log4f + ...} P.(z)
24 ^ K 1 1920 K
\2 „,2 2
{1 в )2 a2 _i 1 p/3va 2 3p ₂- {i + \
Здесь
v 2]tex + ¦¦¦}
24 {fK)1e 4 {fK)(1-в)/2
24
z = - {fK )(1e)/2 log _KaK
,а x{z) определяется так:
1 2pz + z2 + z p X{z) = log{--:-}
1p
В случае опционов около денег (at the money) получаем следующее выражение:
_a a Гі , \{1 в )2 2 , 1 Рва? , 2 3P2 ,.2_]t , 1
aATM = -JiT) {1 + \ ₂₄ J0 + ₄ J0 + ₂₄ V ]t‘x + -}
Эти формулы являются основным результатом данной модели. Хоть размер этих формул и вызывает подозрения, но на самом-то деле эти формулы вполне завершенные и включают в себя простейшие тригонометрические функции. Применять модель SABR для ванильных опционов очень легко, если эти формулы запрограммированы.

Сложность этих формул необходима для точности оценки. Если опустить часть слагаемых в первой формуле для волатильности, то можно получить ошибку, которая в экстремальных случаях
превышает три процента. Слагаемые на местах, где стоит ...в формуле можно смело опускать, как ведущие к пренебрежимо малым ошибкам.
Отметим, что есть два важных частных случая: в = 1, что соответствует стохастической логнормальной модели, и в = 0 - стохастическая нормальная модель.

Управление риском волатильности

Сложность формул модели затуманивает суть самого ЗЛБКа. Дабы сделать модель более понятной и наглядной давайте поймем, что формулы для волатильности можно аппроксимировать следующим образом:
(K,f) = jOe{1-1(1-вр\) log K + ^[(1-в)2+(2-3р2)А2] log2
при условии, что страйк K не слишком далек от текущей форвардной цены f. Здесь отношение
А = -f-
а измеряет силу ? волатильности волатильности ("волвол") в сравнении с локальной волатильностью jO-в при текущей форвардной цене. Хотя данные соотношения и не рекомендуется использовать для оценки реальных сделок, но они приемлемы для отображения качественного поведения модели SABR.
По мере того, как f меняется в течение торговли, ATM volatility образует кривую, которая называется позвоночником(backbone)(более подробно можно найти в [2]). (см. Рисунок 2.). Т.е. получается след рыночной улыбки волатильностидля различных значений K при каждом фиксированном f. На картинках видна динамика позво-ночникадля двух значений в.

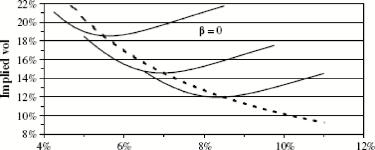
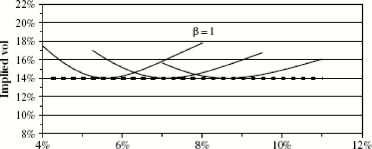
Давайте теперь рассмотрим implied volatility более подробно. Первое слагаемое j представляет собой накопленную волатильность для опционов около денег, т.е. опционов, чей страйк равен текущему форварду.

Таким образом позвоночник, получающийся для опционов у денег на самом деле представляет собой а у (f,f) = у в моделе SABR. Позвоночникпрактически полность определяется в данном случае показателем /3: в = 0 - монотонно скользящий вниз позвоночник, а при в = 1 - практически плоский позвоночник.
Второе слагаемое 1 (1 в РA) log у представляет собой асимметрию(skew), т.е. наклон implied volatility в зависимости от страйка.
2(1 в) log K - это beta skew (бета скошенность), которая убывает, т.к. 0 = в = 1. Она появляется, т.к. локальная волатильность является убывающей функцией форвардной цены. Вторая часть 1 р\ log f - это vanna skew (ванна скошенность), скошенность вызванная корреляцией между волатильностью и ценой б.а. Обычно волатильность и цена актива отрицательно коррелированны, т.е. обычно волатильность а будет уменьшаться по мере роста форвардной цены.

Таким образом становится понятно почему отрицательная корреляция является причиной убывающей vanna skew.
Итак, после выбора в, Р,? и а согласно модели SABR, мы получаем модель, которая очень хорошо отображает все улыбки волатильности на рынке. Также нужно понимать, что мы получили модель, которая достаточна для получения правильных значений волатильности для абсолютно всех страйков и таким образом риски, подсчитанные для одного страйка, будут согласованы с рисками для другого страйка. Опустим пока А риск и подсчитаем остальные риски. Обозначим: BS(f,K,ay,t_ex) -формула Блэка-Шоулза для опциона колл.

Согласно модели SABR, цена колла V_caii = BS(f, K, ар(K,f ),t_ex), где волатильность представлена полученными выше результатами. Тогда можно получить следующие значения для рисков vega, vanna и volga:
_dVcaii dBS ар (K,f)
vega =
да дав ар(f,f)
dVcaii dBS дар (K,f,a,e,P,v)
vanna=
др да
др
, = д?саи = дBS дар(K,f,a,e,P,v)
vOLga *
д? дар д?
Из самого определения легко понять, что vega - риск изменения цены при изменении а, vanna - риск увеличения скошенности, а volga - риск того, что улыбка станет более отчетливой. Эти риски можно хеджировать покупкой или продажей опционов вне денег.

Список литературы

[1] John C. Hull Options, Futures, and Other Derivatives
[2] P.Hagan, D.Kumar, A.Lesniewski, D.Woodward Managing Smile Risk
[3] B.Dupire Pricing with a smile
[4] B.Dupire Pricing and hedging with smiles

Содержание раздела