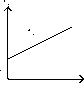
Методы выбора кривых роста
модифицированной экспоненте yt обратной величиной :
yt
= k + a - К.
yt
Используется и другая форма записи уравнения логистической кривой:
Yt =¦
1 + be-a't'
При t^ ордината стремится к нулю, а при t^ да- к асимптоте, равной значению параметра k. Кривая симметрична относительно точки перегиба с координатами: t= ln b: a; yt = k : 2.
Как видно из графика, логистическая функция возрастает сначала ускоренным темпом, затем темп роста замедляется и, наконец, рост почти полностью прекращается, о чем свидетельствует тот факт, что кривая асимптотически приближается к некоторой прямой, параллельной оси абсцисс.
Yk
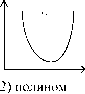
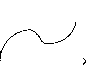
3) полином третьего
порядка yt=a0+a1t; вторг порядка
yt=ao+ait+a2t2 ;
порядка yt=a0+a1t+a2t
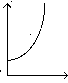
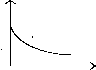
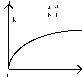
модифицированная экспонента yt=k+axbt
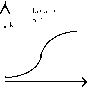
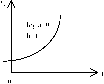
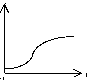
Рисунок 3.1. Кривые роста
С помощью этой функции хорошо описывается развитие новой отрасли (нового производства). Сначала технические методы производства еще недостаточно разработаны, издержки производства
высоки и спрос на рынке на данный товар еще очень мал, поэтому производство развивается медленно. В дальнейшем, благодаря усовершенствованию технических методов изготовления, переходу к массовому производству и увеличению емкости рынка для данного товара производство растет быстрее.
Затем наступает период насыщения рынка, рост производства все более замедляется, и, наконец, почти прекращается. Наступает стабилизация производства на определенном уровне.
Однако выявленные закономерности развития следует обобщать с определенной осторожностью, причем для коротких периодов. Выявленная тенденция развития производства может быть нарушена, например, вследствие технического переворота в данной отрасли или связанной с нею.
Таким образом, мы рассмотрели наиболее часто используемые в экономических исследованиях виды кривых роста. Выявленные особенности и свойства этих кривых могут существенно помочь при решении задачи выбора типа кривой.
Пример 3.1
В таблице 3.1. представлены данные об остатках вкладов населения в банках за 15 месяцев. Остатки вкладов указаны на начало каждого месяца.
| Таблица 3.1. Остатки вкладов населения в банках (млрд. руб.) |
||||||||||||||||||||||||||||||||||||
|
а) линейной моделью y = a + at;
б) параболической моделью yt = ao + at + ait2;
в) показательной моделью yt = a ¦ b
Решение:
а) Для расчета коэффициентов линейного тренда воспользуемся выражениями, полученными из системы нормальных уравнений после переноса начала координат в середину ряда (3.4.).
В таблице 3.2. представлены необходимые вспомогательные вычисления:
| Таблица 3.2. Расчет параметров трендов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
В соответствии с (3.4.):
495958
15
899891
280
= 33063,866 = 3213,896
Следовательно, уравнение линейного тренда имеет вид: jp (= 33063,866 + 3213,896 - t.
Согласно этой модели оценка среднего уровня ряда при t=0 равна 33063,9 млрд. руб., а среднемесячный прирост остатков вкладов населения составляет 3213,9 млрд. руб.
Для прогнозирования на базе полученной модели на одну точку вперед необходимо в нее подставить соответствующее значение временного параметра, т. е. t=8. (Если бы оценки коэффициентов модели были получены без переноса начала координат в середину ряда, то следовало бы подставить в модель значение временного параметра t=16).
Прогноз равен:
у = 33063,866 + 3213,896 - 8
у = 58775 (млрд. руб )
б) Для расчета коэффициентов параболического тренда также воспользуемся выражениями, полученными из системы нормальных уравнений после переноса начала координат в середину ряда (3.5.).
899891
= 3213,896
280
= 153,517 30198,16
15- 9891193 - 280- 495958 15 - 9352 - (280)2
33063,866 - 280-153,517 = 15
Следовательно, уравнение параболического тренда примет вид: у t = 30198,16 + 3213,896t + 153,517t2
Для определения прогноза показателя надо подставить в полученную модель соответствующее значение временного параметра (t=8).
Прогноз равен:
у = 30198,16 + 3213,896 - 8 +153,517 - 82
у = 65734(млрд.руб.)
описываемого
в) Для определения параметров тренда, показательной функцией, воспользуемся (3.9.), (3.6.):
lna
lnb
10,3125
0,1011
154,6876
15
28,29541
280
Проведя потенцирование, получаем:
а=30106,61;
b=1,11
Следовательно, уравнение тренда примет вид: у t = 30106,61 - 1,11'
Согласно этой модели среднемесячный темп роста остатков вкладов населения составлял 111%. В точке, принятой за начало отсчета (t=0), значение тренда равно 30106,61 млрд. руб. Для определения прогноза остатков вклада населения в банках на один месяц вперед подставляем в полученную модель значение t=8: у = 30106,61 1,118 у = 69382 (млрд. руб )
На рисунке 3.2. изображен график исходного временного ряда и выравненные значения уровней, полученные на основе трех трендовых моделей: линейной, параболической и показательной. Графический анализ свидетельствует о том, что линейную модель нельзя признать адекватной. Полученный же на ее основе прогноз будет сильно занижен. Далека от реальности и модель, рассчитанная по показательной функции, а прогноз будет существенно завышен. Ближе всех к фактическим данным ложатся уровни, выравненные по параболической модели, хотя прогноз может быть несколько завышен. Дальнейшее исследование качества полученных моделей должно опираться на показатели, рассматриваемые в главе IV.
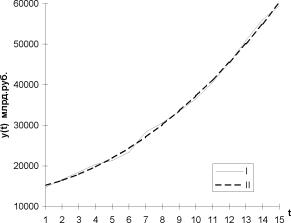
Рисунок 3.2(a). Фактические (I) и выравненные по параболе (II) значения уровней временного ряда.
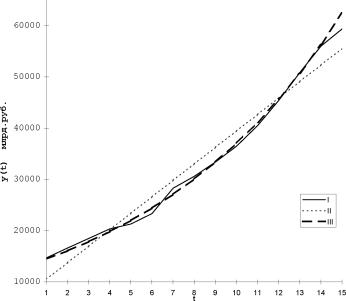
§ 3.2. Методы выбора кривых роста
Существует несколько практических подходов, облегчающих процесс выбора формы кривой роста.
Наиболее простой путь - это визуальный, опирающийся на графическое изображение временного ряда. Подбирают такую кривую роста, форма которой соответствует фактическому развитию процесса. Если на графике исходного ряда тенденция развития недостаточно четко просматривается, то можно провести некоторые стандартные преобразования ряда (например, сглаживание), а потом подобрать функцию, отвечающую графику преобразованного ряда.
В современных пакетах статистической обработки имеется богатый арсенал стандартных преобразований данных и широкие возможности для графического изображения, в том числе в различных масштабах. Все это позволяет существенно упростить для исследователя проведение данного этапа.
В статистической литературе описан метод последовательных разностей, помогающий при выборе кривых параболического типа. Этот метод применим при выполнении следующих предположений: уровни временного ряда могут быть представлены в виде суммы систематической составляющей и случайной компоненты, подчиненной нормальному закону распределения с математическим ожиданием, равным 0, и постоянной дисперсией. Метод предполагает вычисление первых, вторых и т. д. разностей уровней ряда:
AYt = Yt - Yt-i
AVt = AYt-i
и т. д.
Расчет ведется до тех пор, пока разности не будут примерно равными. Порядок разностей принимается за степень выравнивающего полинома.
Существенную помощь при выборе кривых роста из более широкого класса функций может оказать метод характеристик прироста.
Процедура выбора кривых с использованием этого метода включает следующие шаги:
1) выравнивание ряда по скользящей средней;
2) определение средних приростов;
3) вычисление производных характеристик прироста.
Для многих видов кривых были найдены такие преобразования приростов, которые линейно изменялись относительно t или были постоянны. В связи с этим исследование рядов характеристик приростов часто оказывает существенную помощь при определении законов развития исходных временных рядов.
Данный метод является более универсальным по сравнению с методом последовательных разностей.
Однако, чаще всего на практике к выбору формы кривой подходят исходя из значений критерия, в качестве которого принимают сумму квадратов отклонений фактических значений уровня от расчетных, получаемых выравниванием. Из рассматриваемых кривых предпочтение будет отдано той, которой соответствует минимальное значение критерия, т.к. чем меньше значение критерия, тем ближе к кривой ложатся данные наблюдений.
Используя этот подход, следует иметь в виду ряд моментов. Во-первых, к ряду, состоящему из m точек можно подобрать многочлен степени (m-1), проходящий через все m точек.
Кроме того, существует множество многочленов более высоких степеней, также проходящих через все эти точки. Для этих многочленов значение критерия будет равно 0, однако, очевидно, что такая кривая не слишком пригодна как для выделения тенденции, так и для целей прогнозирования.
Также следует учитывать, что за счет роста сложности кривой можно увеличить точность описания тренда в прошлом, однако доверительные интервалы при прогнозировании будут существенно шире, чем у более простых кривых при одинаковом периоде упреждения, например, за счет большего числа параметров.
Таким образом, использование этого подхода должно проходить в два этапа. На первом - происходит ограничение приемлемых функций, исходя из содержательного анализа задачи. На втором - осуществляется расчет значений критерия и выбор на его основе наиболее подходящей кривой роста.
Необходимость содержательного анализа изучаемого процесса развития может быть проиллюстрирована следующими примерами.
Предположим, что на ретроспективном участке ряд динамики может быть хорошо описан с помощью экспоненциальной кривой. Однако, первая половина логистической кривой также представлена экспонентой. Поэтому принять гипотезу об экспоненциальной тенденции ряда в будущем можно только после проведения содержательного анализа, в ходе которого следует дать ответ на вопрос: возможно ли наступление "насыщения" при данной совокупности условий.
Например, процесс производства может быть ограничен материальными ресурсами или производственными мощностями.
Возможна ситуация, когда наилучшей функцией по данному критерию будет признана прямая, однако, полученное на ее основе прогнозное значение будет отрицательным. Если из экономической сути показателя вытекает невозможность отрицательных значений (например, при прогнозировании объема выпускаемой продукции), то, естественно, следует отказаться от этой функции, выбрав менее "удачную" по данному критерию, но более соответствующую содержательному смыслу показателя.
Например, более подходящей в этом случае может оказаться экспоненциальная кривая (3.8.) (при значении параметра в1).
В современных пакетах статистической обработки данных и анализа временных рядов представлен широкий спектр кривых роста, например, в пакете "Олимп", разработанном в МЭСИ и широко используемом в учебном процессе, реализованы 16 кривых роста. Причем, возможны несколько режимов работы, удобных для пользователя.
Можно среди этих кривых выбрать отдельную функцию, и получить подробный протокол, включающий оценки параметров, характеристики остатков, прогнозы, интервальные и точечные. Можно выделить на экране несколько функций, тогда протокол будет содержать оценки параметров всех заказанных функций и значения критерия для каждой из них. В качестве критерия выбирается средняя квадратическая ошибка
е _ Z(yt- y )2
5 = І й
где yt - фактическое значение ряда;
y t - выравненное значение ряда;
n - длина ряда.
Подробный протокол, а также прогнозные значения, на заданное пользователем число временных интервалов, приводятся для функции, отвечающей минимуму указанного критерия. Представляется целесообразным для пользователя на основе выше рассмотренных подходов заранее отвергнуть заведомо непригодные варианты, ограничить поле выбора.
В заключение отметим, что нет "жестких" рекомендаций для выбора кривых роста. Особенно осторожно следует подходить к решению этой задачи при использовании полученной функции для экстраполирования найденных закономерностей в будущее. Применение кривых роста должно базироваться на предположении о сохранении выявленной тенденции в прогнозируемом периоде.
Рассмотренные в данном разделе различные статистические приемы и методы могут помочь исследователю при осуществлении сложного выбора подходящей кривой роста.
Глава 4. Доверительные интервалы прогноза. Оценка адекватности и точности моделей
§ 4.1. Доверительные интервалы прогноза
Заключительным этапом применения кривых роста является экстраполяция тенденции на базе выбранного уравнения. Прогнозные значения исследуемого показателя вычисляют путем подстановки в уравнение кривой значений времени t, соответствующих периоду упреждения.
Полученный таким образом прогноз называют точечным, так как для каждого момента времени определяется только одно значение прогнозируемого показателя.
На практике в дополнении к точечному прогнозу желательно определить границы возможного изменения прогнозируемого показателя, задать вилку возможных значений прогнозируемого показателя, т.е. вычислить прогноз интервальный.
Несовпадение фактических данных с точечным прогнозом, полученным путем экстраполяции тенденции по кривым роста, может быть вызвано:
1) субъективной ошибочностью выбора вида кривой;
2) погрешностью оценивания параметров кривых;
3) погрешностью, связанной с отклонением отдельных наблюдений от тренда, характеризующего некоторый средний уровень ряда на каждый момент времени.
Погрешность, связанная со вторым и третьим источником, может быть отражена в виде доверительного интервала прогноза. Доверительный интервал, учитывающий неопределенность, связанную с положением тренда, и возможность отклонения от этого тренда, определяется в виде:
А+l ± VSp (4Л.Х
где n - длина временного ряда;
L -период упреждения;
€n+l -точечный прогноз на момент n+L;
t а- значение t-статистики Стьюдента;
Sp- средняя квадратическая ошибка прогноза.
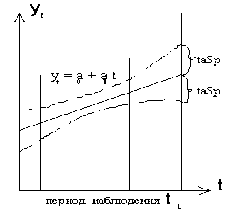
Предположим, что тренд характеризуется прямой:
€t = ao + ait
Так как оценки параметров определяются по выборочной совокупности, представленной временным рядом, то они содержат погрешность. Погрешность параметра а0 приводит к вертикальному сдвигу прямой, погрешность параметра a1- к изменению угла наклона прямой относительно оси абсцисс. С учетом разброса конкретных
S2p можно
реализаций относительно представить в виде:
линий
тренда, дисперсию (ti-1У ±(t -;):
t=1
S2
^ + S
(4.2.),
+ s2
где S(- дисперсия отклонений фактических наблюдений от
расчетных;
ti- время упреждения, для которого делается экстраполяция; ti = n + L ;
t- порядковый номер уровней ряда, t=1,2, ... , n;
t - порядковый номер уровня, стоящего в середине ряда,
t=(n+1):2
Тогда доверительный интервал можно представить в виде:
(4.3.)
К+l ± a svI(-1 f
t=1
Обозначим корень в выражении (4.3.) через К. Значение К зависит только от n и L, т.е. от длины ряда и периода упреждения. Поэтому можно составить таблицы значений К или К*= taK . Тогда интервальная оценка будет иметь вид:
Vn+L ±Sy ¦ K- (4.4.)
Выражение, аналогичное (4.3.), можно получить для полинома второго порядка:
I t4-(21 t2 Y;+nt4
1 + t/
(4.5.)
Я+L ± ta ¦ Sv
или
€n+L ± Sy ¦ K- (4.6.)
Дисперсия отклонений фактических наблюдений от расчетных определяется выражением:
І( - у )2
(4.7.),
t=1
где yt- фактические значения уровней ряда,
yt - расчетные значения уровней ряда, n- длина временного ряда,
k - число оцениваемых параметров выравнивающей кривой.
Таким образом, ширина доверительного интервала зависит от уровня значимости, периода упреждения, среднего квадратического отклонения от тренда и степени полинома.
Чем выше степень полинома, тем шире доверительный интервал при одном и том же значении Sy, так как дисперсия уравнения тренда вычисляется как взвешенная сумма дисперсий соответствующих параметров уравнения
Доверительные интервалы прогнозов, полученных с использованием уравнения экспоненты, определяют аналогичным образом. Отличие состоит в том, что как при вычислении параметров кривой, так и при вычислении средней квадратической ошибки используют не сами значения уровней временного ряда, а их логарифмы.
По такой же схеме могут быть определены доверительные интервалы для ряда кривых, имеющих асимптоты, в случае, если значение асимптоты известно (например, для модифицированной экспоненты).
В таблице 4.1. приведены значения K* в зависимости от длины временного ряда n и периода упреждения L для прямой и параболы. Очевидно, что при увеличении длины рядов (n) значения K* уменьшаются, с ростом периода упреждения L значения K* увеличиваются. При этом влияние периода упреждения неодинаково для различных значений n : чем больше длина ряда, тем меньшее влияние оказывает период упреждения L.
Таблица 4.1.
Значения К* для оценки доверительных интервалов прогноза на основе линейного тренда и параболического тренда при доверительной вероятности 0,9 (7).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| § 4.2. Проверка адекватности выбранных моделей |
Тогда ряд остатков будет получен как отклонения фактических уровней временного ряда (yt) от выравненных, расчетных (y t):
et = yt - У t (490
При использовании кривых роста y t вычисляют, подставляя в уравнения выбранных кривых соответствующие последовательные значения времени.
Принято считать, что модель адекватна описываемому процессу, если значения остаточной компоненты удовлетворяют свойствам
случайности, независимости, а также случайная компонента подчиняется нормальному закону распределения.
При правильном выборе вида тренда отклонения от него будут носить случайный характер. Это означает, что изменение остаточной случайной величины не связано с изменением времени. Таким образом, по выборке, полученной для всех моментов времени на изучаемом интервале, проверяется гипотеза о зависимости последовательности значений et от времени, или, что то же самое, о наличии тенденции в ее изменении. Поэтому для проверки данного свойства может быть использован один из критериев, рассматриваемых в разделе I, например, критерий серий.
Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут не обладать свойствами независимости, т.к. они могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция ошибок.
В условиях автокорреляции оценки параметров модели, полученные по методу наименьших квадратов, будут обладать свойствами несмещенности и состоятельности (с этими свойствами знакомятся в курсе математической статистики). В то же время эффективность этих оценок будет снижаться, а, следовательно, доверительные интервалы будут иметь мало смысла в силу своей ненадежности.
Существует несколько приемов обнаружения автокорреляции. Наиболее распространенным является метод, предложенный Дарбиным и Уотсоном. Критерий Дарбина-Уотсона связан с гипотезой о существовании автокорреляции первого порядка, т.е. автокорреляции между соседними остаточными членами ряда. Значение этого критерия определяется по формуле:
Можно показать, что величина d приближенно равна: d*2(1-n) (4.11),
где г1- коэффициент автокорреляции первого порядка (т.е. парный коэффициент корреляции между двумя рядами e1, e2, ... ,en-1 и e2, e3, ...,
en).
Из последней формулы видно, что если в значениях et имеется сильная положительная автокорреляция (г11), то величина d=0 , в случае сильной отрицательной автокорреляции (r1-1) d=4. При
отсутствии автокорреляции (r10) d=2.
Для этого критерия найдены критические границы, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции. Авторами критерия границы определены для 1, 2,5 и 5% уровней значимости .Значения критерия Дарбина-Уотсона при 5% уровне значимости приведены в таблице 4.2. В этой таблице d1 и d2-соответственно нижняя и верхняя доверительные границы критерия Дарбина-Уотсона; k1 - число переменных в модели; n - длина временного ряда.
Таблица 4.2.
Значения критерия Дарбина-Уотсона di и d2 при 5% уровне
значимости
| n | K= | 1 | K= | 2 | K'= | 3 |
| d: | d2 | d1 | d2 | d1 | d2 | |
| 15 | 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 |
| 16 | 1,1 | 1,37 | 0,98 | 1,54 | 0,86 | 1,73 |
| 17 | 1,13 | 1,38 | 1,02 | 1,54 | 0,9 | 1,71 |
| 18 | 1,16 | 1,39 | 1,05 | 1,53 | 0,93 | 1,69 |
| 19 | 1,18 | 1,4 | 1,08 | 1,53 | 0,97 | 1,68 |
| 20 | 1,2 | 1,41 | 1,1 | 1,54 | 1 | 1,68 |
| 21 | 1,22 | 1,42 | 1,13 | 1,54 | 1,03 | 1,67 |
| 22 | 1,"4 | 1,43 | 1,15 | 1,54 | 1,05 | 1,66 |
| 23 | 1,26 | 1,44 | 1,17 | 1,54 | 1,08 | 1,66 |
| 24 | 1,27 | 1,45 | 1,19 | 1,55 | 1,1 | 1,66 |
| 25 | 1,29 | 1,45 | 1,21 | 1,55 | 1,12 | 1,66 |
| 26 | 1,3 | 1,46 | 1,22 | 1,55 | 1,14 | 1,65 |
| 27 | 1,32 | 1,47 | 1,24 | 1,56 | 1,16 | 1,65 |
| 28 | 1,33 | 1,48 | 1,26 | 1,56 | 1,18 | 1,65 |
| 29 | 1,34 | 1,48 | 1,27 | 1,56 | 1,2 | 1,65 |
| 30 | 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 |
| 31 | 1,36 | 1,5 | 1,3 | 1,57 | 1,23 | 1,65 |
| 32 | 1,37 | 1,5 | 1,31 | 1,57 | 1,24 | 1,65 |
| 33 | 1,38 | 1,51 | 1,32 | 1,58 | 1,26 | 1,65 |
| 34 | 1,49 | 1,51 | 1,33 | 1,58 | 1,27 | 1,65 |
| 35 | 1,4 | 1,52 | 1,34 | 1,58 | 1,28 | 1,65 |
| 36 | 1,41 | 1,52 | 1,35 | 1,59 | 1,29 | 1,65 |