Характеристики точности моделей
Отметим, что большинство программных пакетов статистической обработки данных осуществляет расчет этого критерия (например, ППП Олимп, Мезозавр, Statistica и др.).
При сравнении величины d с d1 и d2 возможны следующие варианты:
1) Если d d1, то гипотеза о независимости случайных отклонений (отсутствие автокорреляции) отвергается;
2) Если d d2, то гипотеза о независимости случайных отклонений не отвергается;
3) Если di d d2, то нет достаточных оснований для принятия решений, т.е. величина попадает в область неопределенности.
Рассмотренные варианты относятся к случаю, когда в остатках имеется положительная автокорреляция.
Когда же расчетное значение d превышает 2, то можно говорить о том, что в et существует отрицательная автокорреляция.
Для проверки отрицательной автокорреляции с критическими значениями d1 и d2 сравнивается не сам коэффициент d, а 4-d.
Для определения доверительных интервалов модели свойство нормальности распределения остатков имеет важное значение. Поскольку временные ряды экономических показателей, как правило, невелики (50), то проверка распределения на нормальность может быть произведена лишь приближенно, например, на основе исследования показателей асимметрии и эксцесса.
При нормальном распределении показатели асимметрии (А) и эксцесса (Э) равны нулю. Так как мы предполагаем, что отклонения от тренда представляют собой выборку из некоторой генеральной совокупности, то можно определить выборочные характеристики асимметрии и эксцесса, а также их среднеквадратические ошибки.
(4.12.)
1Z
n 7=1l!
V t=i у
(4.13.)
t=1
1Z et
V n t=1
a (n - 2 )
(4.14)
(n + 1 )n + 3 )
I 24 n (n - 2 )n - 3 )
(4.15.)
\ (n + 1 )2 (n + 3 )n + 5 ) где А - выборочная характеристика асимметрии;
Э- выборочная характеристика эксцесса;
аА- среднеквадратическая ошибка выборочной характеристики асимметрии;
аэ- среднеквадратическая ошибка выборочной характеристики эксцесса.
Если одновременно выполняются следующие неравенства:
6
|Л|1,5ста ; |Э+-|1,5a
(4.16.),
то гипотеза о нормальном характере распределения случайной компоненты не отвергается.
Если выполняется хотя бы одно из неравенств 6
lAl 2а а;
(4.17.),
2а,
то гипотеза о нормальном характере распределения отвергается. Другие случаи требуют дополнительной проверки с помощью более мощных критериев.
Пример 4.1.
Программа выдала следующие характеристики ряда остатков:
длина ряда n=20;
коэффициент асимметрии А=0,6;
Коэффициент эксцесса Э=0,7.
На основании этих характеристик можно считать, что:
а) случайная компонента подчиняется нормальному закону распределения;
б) случайная компонента не подчиняется нормальному закону распределения;
в) требуется дополнительная проверка характера распределения случайной компоненты.
Решение:
Определим:
6(n - 2)
24n(n-2)(n-3)
(n + 1)2(n + 3)(n + 5)
п ри n= 20
(n + 1)(n + 3)
аA = 0,473; аэ = 0,761
Т. к. одновременно выполняются оба неравенства A 1,5аа (|0,6| 0,71) Ц
1,5аэ (0,7 + 0,29 1,14), то
подчиняется
можно считать, что случайная компонента нормальному закону распределения - вариант ответа а).
§ 4.3. Характеристики точности моделей
Важнейшими характеристиками качества модели, выбранной для прогнозирования, являются показатели ее точности. Они описывают величины случайных ошибок, полученных при использовании модели.
Таким образом, чтобы судить о качестве выбранной модели, необходимо проанализировать систему показателей, характеризующих как адекватность модели, так и ее точность.
О точности прогноза можно судить по величине ошибки (погрешности) прогноза.
Ошибка прогноза- величина, характеризующая расхождение между фактическим и прогнозным значением показателя.
Абсолютная ошибка прогноза определяется по формуле:
А t = УгУі (4.18.),
где Я t - прогнозное значение показателя, yt- фактическое значение.
Эта характеристика имеет ту же размерность, что и прогнозируемый показатель и зависит от масштаба измерения уровней временного ряда.
На практике широко используется относительная ошибка прогноза, выраженная в процентах относительно фактического значения показателя:
(4.19.)
5t = Я Уі - 100 Я
Также используются средние ошибки по модулю (абсолютные и относительные):
где n- число уровней временного ряда, для которых определялось прогнозное значение.
Из (4.18.), (4.19.) видно, что если абсолютная и относительная ошибка больше 0, то это свидетельствует о завышенной прогнозной оценке, если- меньше 0, то прогноз был занижен.
Очевидно, что все указанные характеристики могут быть вычислены после того, как период упреждения уже окончился, и имеются фактические данные о прогнозируемом показателе или при рассмотрении показателя на ретроспективном участке.
В последнем случае имеющаяся информация делится на две части: по первой - оцениваются параметры модели, а данные второй части рассматриваются в качестве фактических. Ошибки прогнозов, полученные ретроспективно (на втором участке) характеризуют точность применяемой модели.
На практике при проведении сравнительной оценки моделей могут использоваться такие характеристики качества как дисперсия (S2) или среднеквадратическая ошибка прогноза (S):
S(y t- yt )2
S2 = -; S = Vs2 (4.21.).
n
Чем меньше значения этих характеристик, тем выше точность модели.
О точности модели нельзя судить по одному значению ошибки прогноза. Например, если прогнозная оценка месячного уровня производства в июне совпала с фактическим значением, то это не является достаточным доказательством высокой точности модели.
Надо учитывать, что единичный хороший прогноз может быть получен и по плохой модели, и наоборот.
Следовательно, о качестве применяемых моделей можно судить лишь по совокупности сопоставлений прогнозных значений с фактическими.
Простой мерой качества прогнозов может стать ^-относительное число случаев, когда фактическое значение охватывалось интервальным прогнозом:
ц = ~JP~ (4.22.),
р+q
где р- число прогнозов, подтвержденных фактическими
данными;
q- число прогнозов, не подтвержденных фактическими данными.
Когда все прогнозы подтверждаются, q=0 и q=1.
Если же все прогнозы не подтвердились, то р=0 и q=0.
Отметим, что сопоставление коэффициентов q для разных моделей может иметь смысл при условии, что доверительные вероятности приняты одинаковыми.
Глава 5. Использование адаптивных методов в экономическом
§ 5.1. Сущность адаптивных методов
В настоящее время одним из наиболее перспективных направлений исследования и прогнозирования одномерных временных рядов являются адаптивные методы.
При обработке временных рядов, как правило, наиболее ценной является информация последнего периода, т.к. необходимо знать, как будет развиваться тенденция, существующая в данный момент, а не тенденция, сложившаяся в среднем на всем рассматриваемом периоде. Адаптивные методы позволяют учесть различную информационную ценность уровней временного ряда, степень устаревания данных.
Прогнозирование методом экстраполяции на основе кривых роста в какой-то мере тоже содержит элемент адаптации, поскольку с получением свежих фактических данных параметры кривых пересчитываются заново. Поступление новых данных может привести и к замене выбранной ранее кривой на другую модель. Однако степень адаптации в данном случае весьма незначительна, кроме того, она падает с ростом длины временного ряда, т.к. при этом уменьшается весомость каждой новой точки.
В адаптивных методах различную ценность уровней в зависимости от их возраста можно учесть с помощью системы весов, придаваемых этим уровням.
Оценивание коэффициентов адаптивной модели обычно осуществляется на основе рекуррентного метода, который формально отличается от метода наименьших квадратов, метода максимального правдоподобия и других методов тем, что не требует повторения всего объема вычислений при появлении новых данных.
Важнейшим достоинством адаптивных методов является построение самокорректирующихся моделей, способных учитывать результат прогноза, сделанного на предыдущем шаге. Пусть модель находится в некотором состоянии, для которого определены текущие значения ее коэффициентов. На основе этой модели делается прогноз. При поступлении фактического значения оценивается ошибка прогноза (разница между этим значением и полученным по модели).
Ошибка прогнозирования через обратную связь поступает в модель и учитывается в ней в соответствии с принятой процедурой перехода от одного состояния в другое. В результате вырабатываются компенсирующие изменения, состоящие в корректировании параметров с целью большего согласования поведения модели с динамикой ряда.
Затем рассчитывается прогнозная оценка на следующий момент времени, и весь процесс повторяется вновь.
Таким образом, адаптация осуществляется итеративно с получением каждой новой фактической точки ряда. Модель постоянно впитывает новую информацию, приспосабливается к ней и поэтому отражает тенденцию развития, существующую в данный момент.
На рисунке приведена общая схема построения адаптивных моделей прогнозирования.
Скорость(быстроту) реакции модели на изменения в динамике процесса характеризует так называемый параметр адаптации. Параметр адаптации должен быть выбран таким образом, чтобы обеспечивалось адекватное отображение тенденции при одновременной фильтрации случайных отклонений.
Значение параметра адаптации может быть определено на основе эмпирических данных, выведено аналитическим способом или получено на основе метода проб.
В качестве критерия оптимальности при выборе параметра адаптации обычно принимают критерий минимума среднего квадрата ошибок прогнозирования.
На основе рассмотренных особенностей дадим определение группы методов прогнозирования, объединенных общим названием адаптивные.
Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся (самонастраивающиеся) экономико -математические модели, которые способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда. Благодаря указанным свойствам адаптивные методы особенно удачно используются при краткосрочном прогнозировании (при прогнозировании на один или на несколько шагов вперед).
Обозначения:
y(t)- фактические уровни временного ряда;
€T(t)- прогноз, сделанный в момент t на т единиц времени (шагов) вперед;
et+i- ошибка прогноза, полученная как разница между фактическим и прогнозным значением показателя в точке (t+1).
Рассмотрим наиболее простые, из многочисленного класса адаптивных методов, - методы, использующие процедуру экспоненциального сглаживания.
§ 5.2. Экспоненциальное сглаживание
Для экспоненциального сглаживания ряда используется рекуррентная формула
St = ayt + pSt-i (5.1.),
где St- значение экспоненциальной средней в момент t;
a- параметр сглаживания, a^onst, 0a1;
Р= 1-a.
Если последовательно использовать соотношение (5.1.), то экспоненциальную среднюю St можно выразить через предшествующие значения уровней временного ряда. При п^-да
S, = а^р- У, - (5.2.)
i=0
Таким образом, величина St оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от возраста наблюдений).
Именно поэтому величина названа экспоненциальной средней.
Например, пусть a=0,3. Тогда вес текущего наблюдения yt будет равен a=0,3, вес предыдущего уровня yt-1 будет соответствовать axp=0,3x0,7=0,21; для уровня yt-2 вес составит axp2=0,147; для yt-3 вес axp3=0,1029 и т.д.
Предположим, что модель временного ряда имеет вид:
yt=a1+et.
Английский математик Р. Браун показал, что математические ожидания ряда и экспоненциальной средней совпадут, но в то же время дисперсия экспоненциальной средней D[St] меньше дисперсии временного ряда (а2)
ли=(5-3.)
Из (5.3.) видно, что при высоком значении a дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением a дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым,
экспоненциальная средняя начинает играть роль фильтра,
поглощающего колебания временного ряда.
Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением а (согласно(5.2.)), с другой стороны, для сглаживания случайных отклонений величину а нужно уменьшить. Эти два требования находятся в противоречии.
Поиск компромиссного значения параметра сглаживания а составляет задачу оптимизации модели.
Иногда поиск этого значения параметра осуществляется путем перебора. В этом случае в качестве оптимального выбирается то значение а, при котором получена наименьшая дисперсия ошибки.
Например, при построении этих моделей с помощью пакета Мезозавр в меню предусмотрена ветвь оптимизация, реализующая поиск значения по этой схеме.
При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид:
yt = ai,t + et,
где a1jt - варьирующий во времени средний уровень ряда,
et- случайные неавтокоррелированные отклонения с нулевым математическим ожиданием и дисперсией а2.
Прогнозная модель определяется равенством:
М* ) = ^,
где €T(t)- прогноз, сделанный в момент t на т единиц времени (шагов) вперед;
a11 - оценка a11 (знак Л над величиной означает оценку).
Единственный параметр модели a1t определяется экспоненциальной средней:
a1,t = St
a1,o=St
Выражение (5.1.) можно представить по-другому,
перегруппировав члены:
St = St-1 + а (yt - St-1) (5.4.)
Величину (yt - St-1) можно рассматривать как погрешность прогноза. Тогда новый прогноз St получается в результате корректировки предыдущего прогноза с учетом его ошибки.
В этом и состоит адаптация модели.
Экспоненциальное сглаживание является примером простейшей самообучающейся модели. Вычисления чрезвычайно просты, выполняются итеративно, причем массив прошлой информации уменьшен до единственного значения St-1.
§ 5.3. Адаптивные полиномиальные модели
Понятие экспоненциальной средней можно обобщить в случае экспоненциальных средних более высоких порядков.
Выравнивание p-го порядка:
S( ]=a-Stp-l)+^-S() (5.5.)
является простым экспоненциальным сглаживанием,
примененным к результатам сглаживания (р-1)-го порядка.
Если предполагается, что тренд некоторого процесса может быть описан полиномом степени n, то коэффициенты предсказывающего полинома могут быть вычислены через экспоненциальные средние соответствующих порядков.
В случае, когда исследуемый процесс, состоящий из детерминированной и случайной компоненты, описывается полиномом n-го порядка, прогноз на т шагов вперед осуществляется по формуле:
Я() = € + а2т + 2 ^ + - - - + 1 ?n+1 - тП где а1,a2,....an+1- оценки параметров.
Фундаментальная теорема метода экспоненциального сглаживания и прогнозирования, впервые доказанная Р. Брауном и Р. Майером, говорит о том, что (n+1) неизвестных коэффициентов полинома n-го порядка а1, а2, ... an+1 могут быть оценены с помощью линейных комбинаций экспоненциальных средних S(i), где i=1^n+1.
Следовательно, задача сводится к вычислению экспоненциальных средних, порядок которых изменяется от 1 до n+1, а затем через их линейные комбинации - к определению коэффициентов полинома.
На практике обычно используются полиномы не выше второго порядка. Например, при использовании полинома первого порядка адаптивная модель временного ряда имеет вид: yt = ai,t + a2,t + et (5.7.),
где a1jt - значение текущего t-го уровня; a2,t - значение текущего прироста.
В таблице (5.1.) приведены формулы, необходимые для расчета по этим моделям.
Процедура прогнозирования временных рядов по методу экспоненциального сглаживания сравнительно проста и состоит из следующих этапов:
1. Выбирается вид модели экспоненциального сглаживания, задается значение параметра сглаживания а. При выборе порядка адаптивной полиномиальной модели могут использоваться различные подходы, например, графический анализ, метод изменения разностей и др..
2. Определяются начальные условия. Например, для
полиномиальной модели первого порядка необходимо определить a1j0;
а.2,0.
Чаще всего в качестве этих оценок берут коэффициенты соответствующих полиномов, полученные методом наименьших квадратов. Начальные условия для модели нулевого порядка обычно получают усреднением нескольких первых уравнений ряда.
Зная эти оценки, с помощью указанных в таблице формул находят начальные значения экспоненциальных средних.
3. Производится расчет значений соответствующих экспоненциальных средних.
4. Находятся оценки коэффициентов модели.
5. Осуществляется прогноз на одну точку вперед, находится отклонение фактического значения временного ряда от прогнозируемого. Шаги с 3 по 5 данной процедуры повторяются для всех tn , где n- длина ряда.
6. Окончательная прогнозная модель формируется на последнем шаге в момент t=n. Прогноз получается на базе выражения (5.6.) путем подстановки в него последних значений коэффициентов и времени упреждения т.
К положительным особенностям рассмотренных моделей следует отнести то, что при поступлении новой, свежей информации расчеты повторять не придется. Достаточно принять в качестве начальных условий последние значения функций сглаживания S() и продолжить вычисления.
Таблица 5.1.
Основные формулы для прогнозирования по адаптивным полиномиальным моделям
| Степень модели |
Начальные условия |
Экспонен циальные средние |
Оценка коэффициентов |
Модель прогноза |
| n=0 | s(i) - a ^0 d1,0 | St(1) -ayt +ps(-\ | у и |
y т (t) - a 1,t |
| n=1 | s 011- i,0 -?o,0 s 02'- *1,0 - | sW-ayt + в S(1-1 Sf1 - a St1) + в S(21) |
€1,t - 2S(1) - S(2) *2,t -a( - S? ) |
T)- *1,t + *1j T |
| n=2 | S()-*,0 -в*2,0 +eaa*h,0 s02) - €,0 - 04+^(4 *3,0 S(3) € 3e€ , 3e(4- 3a) € S0 *1,0 „ *2,0 + -2 *3,0 a 2a |
St1)-ay, + вSt1-1 St(2)-aS(1) + eS(21) S,(3) -a S(2) + в S(3-) |
*1,, - 3(s,(,) - S,2))+ S,3) *2,, - a [(6 -5a)S® -- 2(5 - 4a)Sf + (4 - 3a)S® ] *3,t -y [s™ - 2S,2) + S,3) ] |
+ + ~+ 4 |
§ 5.4. Адаптивные модели сезонных явлений
Многие экономические временные ряды содержат периодические сезонные колебания. Такие ряды могут быть описаны моделями двух типов- моделями с мультипликативными (5.8.) и с аддитивными коэффициентами сезонности (5.9.):
yt = а1д - ft + et (5.8.)
yt = a, t+gt + e (5.9.X
где а 1t- характеристика тенденции развития,
g^g^,...^^- аддитивные коэффициенты сезонности, ft,ft_1,...,fr_e+1- мультипликативные коэффициенты сезонности,
е- количество фаз в полном сезонном цикле (для ежемесячных наблюдений е=12, для квартальных -е = 4),
et- случайная компонента с нулевым математическим ожиданием. Очевидно, что можно составить множество адаптивных сезонных моделей, перебирая различные комбинации типов тенденций в сочетании с сезонными эффектами аддитивного и мультипликативного вида. Выбор той или иной модели будет продиктован характером динамики исследуемого процесса. В качестве примера рассмотрим модель Уинтерса с линейным характером тенденции и мультипликативным сезонным эффектом.
Эта модель является объединением двухпараметрической модели линейного роста Хольта и сезонной модели Уинтерса, поэтому ее чаще всего называют моделью Хольта-Уинтерса.
Прогноз по модели Хольта-Уинтерса на т шагов вперед определяется выражением:
€т()=(( +т - a2,t )^?_е+т (5.10.)
Обновление коэффициентов осуществляется следующим образом:
= a +(1 _ a )(a1,t _1 + a2,t_1)
(5.11.)
ft =a2 + (1 a2 )ft_e
At
A,t = a3 (at1,t _ at1,t_1 ) + (1 _ a3 )at2,t_1
0 a1,a2,a3 1
Из (5.11.) видно, что €1t является взвешенной суммой текущей
yt
полученной путем очищения от сезонных колебаний
оценки
t _е
фактических данных yt и предыдущей оценки €11_1. В качестве коэффициента сезонности ft берется его наиболее поздняя оценка, сделанная для аналогичной фазы цикла f _е ).
Затем величина a 1t, полученная по первому уравнению,
используется для определения новой оценки коэффициента сезонности по второму уравнению. Оценки a2t модифицируются по процедуре,
аналогичной экспоненциальному сглаживанию.
Оптимальные значения для а1, а2,а3 Уинтерс предлагает находить экспериментальным путем, задавая сетку значений этих параметров. Критерием сравнения при этом выступает стандартное отклонение ошибки.
Адаптивные сезонные модели являются важной составной частью современных пакетов прикладных программ, ориентированных на решение задач прогнозирования.
Пример 5.1
Рассчитать экспоненциальную среднюю для временного ряда курса акций фирмы IBM. В качестве начального значения экспоненциальной средней взять среднее значение из 5 первых уровней ряда. Расчеты провести для двух различных значений параметров адаптации а:
а) а=0,1;
б) а=0,5.
Сравнить графически исходный временной ряд и ряды экспоненциальных средних, полученные при а=0,1 и а=0,5. Указать, какой ряд носит более гладкий характер
Таблица 5.2.
| Курс акций фирмы IBM (долл.) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 5 1
1. Определим S0 = - ^ yt = - (510 + 497 + 504 + 510 + 509) = 506
5 t=i 5
Найдем значения экспоненциальной средней при а=0,1. St=axt+(1-a)St-1. а=0,1- по условию;
S1=ax1+(1-a)S0;
S1=0,1x510+0,9x506=506,4;
S2=ax2+(1-a)Sb S2=0,1x497+0,9x506,4=505,46; S3=ax3+(1-a)S2; S3=0,1x504+0,9x505,46=505,31 и т.д. Результаты расчетов представлены в таблице 5.3. a=0,5- по условию.
S1=ax1+(1-a)S0;
S1=0,5x510+0,5x506=508;
S2=ax2+(1-a)S1; S2=0,5x497+0,5x508=502,5 и т.д.
Результаты расчетов представлены в таблице:
Экспоненциальные средние
| Таблица 5.3. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
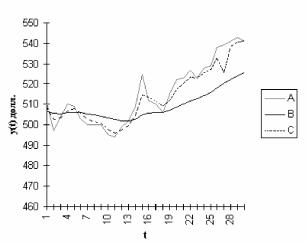
При а=0,1 экспоненциальная средняя носит более гладкий характер, т. к. в этом случае в наибольшей степени поглощаются случайные колебания временного ряда.
Выводы
Статистические методы все шире проникают в экономическую практику. С развитием компьютеров, распространением пакетов прикладных программ эти методы вышли за стены учебных и научноисследовательских институтов. Они стали важным инструментом в деятельности аналитических, плановых, маркетинговых отделов различных фирм и предприятий.
При прогнозировании часто исходят из того, что уровни временных рядов экономических показателей, состоят из четырех компонент: тренда, сезонной, циклической и случайной составляющих. В зависимости от способа сочетания этих компонент модели временных рядов делятся на аддитивные, мультипликативные или модели смешанного типа.
Обобщенными показателями динамики развития экономических процессов являются средний прирост, средний темп роста и прироста. При выполнении ряда предпосылок эти показатели могут быть использованы в приближенных, простейших способах прогнозирования, предшествующих более глубокому количественному и качественному анализу.
Распространенным приемом при выявлении тенденции развития является выравнивание временных рядов, в частности, с помощью скользящих средних.Скользящие средние позволяют сгладить как случайные, так и периодические колебания, выявить имеющуюся тенденцию в развитии процесса.
Выравнивание временных рядов может осуществляться с помощью тех или иных функций времени- кривых роста. Применение кривых роста должно базироваться на предположении о неизменности, сохранении тенденции как на всем периоде наблюдений, так и в прогнозируемом периоде.
Прогнозные значения по выбранной кривой роста вычисляют путем подстановки в уравнение кривой значений времени, соответствующих периоду упреждения. Полученный таким образом прогноз называется точечным. В дополнении к точечному прогнозу желательно задать диапазон возможных значений прогнозируемого показателя, т. е. вычислить прогноз интервальный (определить доверительный интервал). Доверительный интервал учитывает неопределенность, связанную с положением тренда (погрешность оценивания параметров кривой), и возможность отклонения от этого тренда.
Для того, чтобы обоснованно судить о качестве полученной модели необходимо проверить адекватность этой модели реальному процессу и проанализировать характеристики ее точности. Проверка адекватности строится на анализе случайной компоненты и базируется на использовании ряда статистических критериев. Показатели точности описывают величины случайных ошибок, полученных при использовании модели. Все характеристики точности могут быть вычислены после того, как период упреждения уже окончился, или при рассмотрении показателя на ретроспективном участке.
Одно из перспективных направлений развития краткосрочного прогнозирования связано с адаптивными методами. Эти методы позволяют строить самокорректирующиеся модели, способные оперативно реагировать на изменение условий. Адаптивные методы учитывают различную информационную ценность уровней ряда, "старение" информации. Все это делает эффективным их применение для прогнозирования неустойчивых рядов с изменяющейся тенденцией.
В заключении отметим, что не может быть чисто формальных подходов к выбору методов и моделей прогнозирования. Успешное применение статистических методов прогнозирования на практике возможно лишь при сочетании знаний в области самих методов с глубоким знанием объекта исследования, с содержательным экономическим анализом.
Список рекомендуемой литературы
1. Кендэл М. Временные ряды. М., "Финансы и статистика", 1981.
2. Кильдишев Г. С., Френкель А. А. Анализ временных рядов и прогнозирование. М., "Статистика", 1973.
3. Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования. М., "Статистика", 1979.
4. Половников В. А. Анализ и прогнозирование транспортной работы морского флота. М., "Транспорт", 1983.
5. Скучалина Л. Н., Крутова Т. А. Организация и ведение базы данных временных рядов. Система показателей, методы определиня, оценки прогнозирования информационных процессов.
ГКС РФ, М., 1995.
6. Статистическое моделирование и прогнозирование. Учебное пособие. (Под ред.
А. Г. Гранберга). М., "Финансы и статистика", 1990.
7. Четыркин Е. Н. Статистические методы прогнозирования. М., "Статистика", 1975.
8. Френкель А. А. Прогнозирование производительности труда: методы и модели. М., "Экономика", 1989.
9. Экономико-математические методы и прикладные модели. (Под ред. В.В.
Федосеева). М., Юнити, 1999.