Производящая функция, моменты
Параметр c найдём из условия (3.26): 1 = J f(x)dx = J 0dx +J -^-5 dx
c
= , откуда c = 2,5 . Таким образом, f (x) =
Функцию распределения найдем по формуле (3.24): F (x) = J f (z)dz = J 0dz = 0 при x 1,
x 1 x x
F(x) = J f (z)dz = J f (z)dz + J f (z)dz = J -
Ж
Таким образом, F (x) =
2,5 x2,5
Ж
0, x 1,
2,5 x1.
3,5’
1 1
0, x 1,
25 dt = J_
z3,5 = t2,5
= 1 25 при x ^ 1.
1-
1
,2,5,
x 1.
0,5 ~’5
По условию P{X ^ xmin} = 1 P{X xmin} = 1 F(xmin) = 0,5, откуда F(xmin) = 0,5, т. е.
1 n г 2,5 о _ ! ln 2 0,693 0,28 o0 n
1 ~2^ = 0, 5 или xmin= 2, поэтому ln xmin= -jy ~ 028, значит xmin e ’ ~ 1 32 - ?
xmin 7 7
204. Годовой доход случайно выбранного налогоплательщика описывается случайной величиной X с плотностью распределения
0, x 1,
f(x) =
-С4, x ^ 1.
x
Найти значение параметра c, средний годовой доход и среднее квадратичное отклонение годового дохода. Определить размер годового дохода xmin, не ниже
которого с вероятностью 0,6 окажется годовой доход случайно выбранного налогоплательщика .
205. Плотность распределения случайной величины X
[ax, x ? [0, 2],
X(x) = [ 0, x ? [0; 2].
Найти значение параметра a, функцию распределения Fx (x), MX и DX, построить графики функций X (x) и Fx (x). Вычислить P{| X MX | 0, 5} двумя способами: используя X (x) и Fx (x), отметить эту вероятность на обоих графиках.
206. Найти плотность распределения, математическое ожидание и дисперсию случайной величины с функцией распределения
0, x 2,
4+0,5, 2x2,
4 1 x^2.
О
непрерывная случайная величина, X
X-MX aX
207. Пусть X
. Доказать, что
M X = 0, D X = 1.
Равномерное распределение
208. Случайная величина X ~ R[0; 100]. Найти вероятности P{X 10}, P{40 X 90}, P{X = 50} и P{X 50 | X 80}, а также математическое ожи
дание и дисперсию этой случайной величины.
РЕШЕНИЕ. P{X 10} = 1 - P{X 10} = 1 - F (10) = 1 - 10-L = 0,9; P{40 X 90} = F (90)-F (40) =
=-90-- - ^0_0_=0^ 5, p{x=50}=0, P{X50 | X 80}=-; MX==50; DX=(100 0) = 2500 100-0 100-0 L J L 1 J 8 2 12 3
209. Найти вероятность того, что сумма значений случайной величины X, определённой в задаче 208, в двух независимо проведённых опытах превысит 80.
Задачу решить графически.
210. Все значения равномерно распределённой случайной величины расположены на отрезке [2; 8].
Найти математическое ожидание и дисперсию этой случайной величины, а также вероятности её попадания на отрезок [6; 9] и в интервал (3; 5).
211. При выяснении причин недостачи драгоценных металлов в ювелирном магазине установлено, что их взвешивание производится на весах, цена деления которых равна 0,1 г, а показания весов округляются при взвешивании до ближайшего деления их шкалы, причём округления на любые значения от - 0,05 до 0,05 равновероятны.
Оценить возможность возникновения ошибки более, чем на 0,03 г, вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение потерь.
212. Решить задачи 47 - 56, пользуясь равномерным распределением вероятностей.
213. Вывести формулы для математического ожидания и дисперсии равномерного распределения (см. табл.
3.2).
(J}-*)(b+a) a+b _
J xf (x)dx = J x dx
DX =
MX =
РЕШЕНИЕ.
+ж
a 2(b-a) 2(J_a) 2 '
b3-a3 (a+b)2 = - _aT (b2 + ab + a2)
-a 2 3'u
J x f (x)dx - (MX)2 =J x2 --- dx - = -j- '
-ж a
a 2-2ab+b 2 = 4b 2 + 4ab+4a 2 3a2 -6ab+3b 2 = a2-2ab+b2 (b-a)
x
-a 3
3 (j-О)
a 3(b a) I 2
?
4 12 12 12 12
214. ПРАВИЛО ТРЁХ сигм.
Случайная величина X ~ R(a; b). Найти
P{|X - MX| 3aX}.
215. Случайные величины X ~ R(a; b) и Y ~ R(c; d) независимы.
Найти M(XY) и D(XY).
Показательное распределение
216. Обычно папа ругает Петю за принесённую двойку около 6 мин.
На этот раз нотация длится больше 6 мин. Найти математическое ожидание и дисперсию
длительности нотации. Определить, с какой вероятностью папа закончит читать нотацию в течение ближайшей минуты?
РЕШЕНИЕ. Длительность нотации X можно считать распределённой по показательному закону. По условию обычная средняя длительность нотации (или её математическое ожидание) со-
1 11
ставляет MX = 6 мин. Но для показательного распределения MX = , откуда р = ^ . Дис-
1 1"
. 1^61 = 36 . Вероятность того, что папа
1
персия длительности нотации при этом равна DX = *¦
р2
закончит читать нотацию в течение ближайшей (седьмой) минуты при условии, что нотация
к , г , , P{(X 7)n(X 6)} P{6X 7} F (7)-F (6)
длится больше 6 мин, равна P{X 71X 6} = u P{X 6}- = P{X 6} = \_р (6) =
1/6 и 0,154. ?
217. Случайная величина X ~ Exp(p = 2).
Определить вероятности P{X 1}, P{X 2}, P{X 1}, P{X = 3} и P{X 1 | X 3}, математическое ожидание и дисперсию этой случайной величины.
218. Обычно брокер получает от своего клиента приказы об операциях на фондовой бирже раз в неделю.
Найти вероятность того, что сегодня поступит приказ, если последний приказ поступил два дня назад. Поток приказов считать простейшим.
219. Обычно совещание длится час.
На этот раз за час оно не закончилось. Какова вероятность того, что оно закончится в ближайшие 15 мин.
Длительность совещания распределена по показательному закону.
220. Длительность междугородних телефонных разговоров распределена примерно по показательному закону, разговор продолжается в среднем 3 мин. Найти вероятность того, что очередной разговор будет продолжаться более 3 мин.
Определить долю разговоров, которые длятся менее 1 мин. Найти вероятность того, что разговор, который длится уже 10 мин, закончится в течение ближайшей минуты, а также математическое ожидание и дисперсию длительности разговора.
221. Время, необходимое для оформления договора, является случайной величиной, распределённой по показательному закону с параметром Л = 0,3-.
Найти вероятность того, что оформление договора займёт менее 7 ч. Найти среднее время оформления договора.
222. Случайная величина X ~ Exp(p).
Найти P{a ^ X ^ b}.
223. Случайная величина X ~ Exp(p). Найти: а) P{0 ^ X ^ т},
б) P{t X t + т | X ^ t}.
224. Вывести формулы для математического ожидания и дисперсии показательного распределения (см. табл.
3.2).
Нормальное распределение
225. Значения теста IQ (коэффициента интеллекта) Стэнфорда - Бине распределены приблизительно по нормальному закону с математическим ожиданием a = 100 и средним квадратичным отклонением а = 16. Записать выражения для функции распределения коэффициента интеллекта и плотности его распределения.
Построить графики этих функций.
а) б)
Рис. 3.1. График функции распределения (а) и кривая распределения (б) в задаче 225
226. В условиях задачи 225 найти долю людей, у которых коэффициент интеллекта окажется: а) меньше 60; б) меньше 75; в) меньше 95; г) меньше 100; д) меньше 120; е) в пределах от 80 до 120.
227. В условиях задачи 225 найти долю людей, у которых коэффициент интеллекта отклонится от 100 менее, чем на 48.
228. В условиях задачи 225 найти вероятность того, что из шести независимо отобранных человек у двоих коэффициент интеллекта будет выше 92.
229. Случайная величина X ~ N (а = 0; а = 1). Построить кривую распределения этой случайной величины, график её функции распределения.
Найти координаты плотности распределения f(x) и функции распределения F(x) при x = 1; 1; 2,25. Вычислить и указать на обоих графиках следующие вероятности:
P{X 1}; P{X 1}; P{X| 1}; P{| X | 3}; P{0X3} .
230. Случайная величина X ~ N (a = 1; а = 1).
Найти вероятности P{X 2}, P{X 2}, P{0 X 2} и P{X 2 | X 0}.
231. Правило трёх сигм. Случайная величина X ~ N (а; а).
Найти P{|X MX| 3aX}.
232. Доказать, что для случайной величины X~N (а; а) P{aX 0} =
=P{a^X0}=P{aX^ 0}=P{a^X^0}=Ф0 (а)Ф0 (аа), P{|X а |Д} = 2Ф0 .
233. Случайная величина X ~ N (а = 2; а = 3).
Найти вероятности P{X 1}, P{2 X ^ 2}, P{X 2} и P{X 2 | X 0}. Записать правило трёх сигм для этой случайной величины.
234. Вывести формулы для математического ожидания и дисперсии нормального распределения (см. табл.
3.2).
235. Текущая цена акции может быть приближена нормальным распределением с математическим ожиданием 15,28 руб. и средним квадратичным отклонением 0,12 руб.
Рассчитать вероятности того, что цена акции окажется: а) не ниже 15,50 руб.; б) не выше 15,00 руб.; в) между 15,10 руб. и 15,40 руб.; г) между 15,05 руб. и 15,10 руб.
236. Цена некоторой акции распределена нормально. В течение последнего года в 20% рабочих дней цена была меньше 20 руб., а в 75% рабочих дней она была больше 25 руб.
Найти математическое ожидание и среднее квадратичное отклонение цены этой акции.
237. Из данных, полученных от руководства цеха при его проверке, следует, что брак составляет 5% всей выпускаемой продукции. По данным, полученным из технической документации, установлено, что размер продукции представляет собой случайную величину, распределённую по нормальному закону с математическим ожиданием, равным 10 мм, и средним квадратичным отклонением, равным 0,2 мм. Величина максимально допустимого отклонения размера детали от номинального, при котором деталь ещё считается годной, составляет 0,3 мм.
Оценить с помощью вероятности достоверность информации, полученной от руководства цеха о качестве выпускаемой продукции.
238. При расследовании причин аварии было установлено, что она могла произойти из-за установки на автомобиль детали, размеры которой выходят за пределы допустимого интервала (15 мм; 25 мм). Известно, что размер деталей, поступающих на конвейер автозавода, представляет собой случайную величину, распределённую по нормальному закону с математическим ожиданием, равным 20 мм, и средним квадратичным отклонением, равным 5 мм.
Оценить вероятность того, что причиной аварии послужила установка на автомобиль детали нестандартного размера.
239. ПРАВИЛО шести сигм.
Крупнейшие мировые корпорации при статистическом контроле качества продукции переходят в настоящее время на правило шести сигм. Напомним, что правило трёх сигм означает, что некачественная продукция (не попадающая в интервал (MX-3а^; МХ+Зо^)) составляет
100 99,73 = 0,27%, т. е. на каждые 10 000 единиц продукции допустимо изготовление не более, чем 27 некачественных. Пояснить, в чём заключается правило шести сигм: какова допустимая доля некачественной продукции?
Логнормальное распределение
240. Указать недостатки использования нормального распределения для приближения распределений цен активов.
Объяснить, как логнормальное распределение используется для преодоления этих недостатков.
241. Вывести формулы для математического ожидания и дисперсии логнормального распределения (см. табл.
3.2).
242. Статистика по вкладам населения в некоторый банк говорит о том, что размер вклада случайно выбранного клиента распределён по логнормальному закону с параметрами a = 1 200 ден. ед., а = 2 ден. ед.
Определить: а) средний размер вклада; б) долю клиентов, размер вклада которых составляет не менее 1 000 ден. ед.
243. Месячный доход случайно выбранной семьи из некоторой социальной группы описывается логнормальным законом распределения с математическим ожиданием 1 000 ден. ед. и средним квадратичным отклонением 600 ден. ед.
Найти долю семей, имеющих доход менее 1 500 ден. ед.
Другие законы распределения
244. Вычислить: а) P{x20109}; б) P{x^ 28,4}; в) P{8,26 ^ хэд 31,4}; г) P{x40 10,9}; д) P{x20 28,4}; е) P{8,26 ^ х|0 31,4}.
245. Найти: а) P{|T10|2,23}; б) P{-1,81T103,17}; в) P{-1,81T403,17}.
246. Найти P{|F3.16|3,24}.
| /с.і |
| ,і і Рис. 3.2. График плотности треугольного распределения |
Найти функцию распределения, математическое ожидание и дисперсию этой случайной величины.
248. Распределение Рэлея. Найти функцию распределения и математическое ожидание случайной величины X, плотность распределения которой имеет вид
0, x 0,
-e 2a^
x ^0.
РЕШЕНИЕ. Очевидно, F (x) = 0 при x 0. При x ^ 0 F(x)= J f (r)dr = J 0dr +
| x - ( r ) dr = J e (aV2) d +J e 2a2 dr =J e laV2 2r 0 0 2a rj2 = e a- 0=e 2a 2 +e0 = 1e 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
t {по частям} = 2 u 2 du = 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 0 0 +4 |
§3.4. Производящая функция, моменты, МОДА, МЕДИАНА И КВАНТИЛИ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Начальным моментом k -го порядка случайной величины X называется математическое ожидание k -й степени случайной величины X:
vk(X) = M(Xk), k = 0,1,2.... (3.33)
Центральным моментом k -го порядка случайной величины X называется математическое ожидание k -й степени отклонения случайной величины X от своего математического ожидания:
Fk (X) = M[(X MX)k ], k = 0,1,2,.... (3.34)
Справедливы следующие выражения для центральных моментов:
р0 (X) = v0 (X) = 1; (3.35)
p1(X) = 0; (3.36)
р2 (X) = ? 2 (X) (X); (3.37)
д3 (X) = V3(X) - 3v1 (X)?2 (X) + 2vJ (X); (3.38)
д4 (X) = ?4 (X) - 4?1 (X)?3 (X) + 6?2 (X)?2 (X) - 3?4 (X). (3.39)
Производящей функцией случайной величины X называется функция от параметра t (вообще говоря, комплексного), равная
mX (t) = MetX . (3.40)
Как и раньше, если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: m(t) = mX (t).
Начальные моменты случайной величины X выражаются через производные её производящей функции:
для всех k = 0,1,2,...: vk (X) = mX) (0), (3.41)
где mX) (t) k -я производная функции mX (t).
Если t = iu (где i = V1), то производящая функция переходит в характеристическую функцию, широко используемую в фундаментальной теории вероятностей и теории меры. Производящая функция случайной величины обладает следующими свойствами:
mcX (t) = mX (ct); (3.42)
mx+у (t) = mx (t )шу (t) (3.43)
(здесь X, У независимые случайные величины, c неслучайная постоянная).
В качестве показателя центра группирования значений случайной величины, наряду с математическим ожиданием, используются также медиана и мода.
Медианой абсолютно непрерывной случайной величины X называется такое число MeX, что
P{X MeX} = P{X MeX} = 0,5 . (3.44)
Медиана MeX дискретной случайной величины X (заданной рядом распределения (3.9) это любое число, которое находится на отрезке [x^; x^+і ], определяемом из условий
l l+1
Е Pi X 0,5; Е Рг 0,5, (3.45)
i=1 i=1
и называемом медианным. В качестве медианы MeX обычно используют значение, получаемое линейной аппроксимацией:
lЕ Pi
xl+1 xl
pl+1
(3.46)
MeX = xi +
i=1
Модой абсолютно непрерывной случайной величины X называется точка локального максимума плотности распределения:
Jx (MoX) = max X (x). (3.47)
x GM
Модой дискретной случайной величины X называется значение этой случайной величины, соответствующее наибольшей вероятности:
MoX = x-, такое, что p- = max p -. (3.48)
i - -
Распределения, имеющие одну моду, называются одномодальными.
Коэффициент асимметрии Ах случайной величины X характеризует скошенность кривой распределения этой случайной величины относительно её математического ожидания и вычисляется по формуле
й3(Х)
(3.49)
Обычно | Ax | 2. Для симметричных распределений = 0, если левая ветвь кривой распределения длиннее правой, то А^ 0, если же левая ветвь кривой распределения короче правой, то Ах о.
Эксцесс Ех случайной величины X характеризует островершинность кривой распределения этой случайной величины по сравнению с кривой нормального распределения и вычисляется по формуле
Е = ^4 (X) 3 ЕХ = 4 3
Обычно 1 ^ Ех ^6 .
Для нормального распределения N(а-о) = 0; если кривая распределения случайной величины X
имеет менее острую вершину, чем кривая нормального распределения, то Ех 0; если кривая распределения случайной величины X имеет более острую вершину, чем кривая нормального распределения, то Ех 0.
Левосторонней критической границей (или квантилью) уровня а случайной величины X называется такое число Ка, что
(3.51)
FX (Ка ) = а,
т. е. P{X Ка } = а .
Правосторонней критической границей уровня а случайной величины X называется такое число Ва, что
FX (Ва) = 1 а, (3.52)
т- е- P{X ^ Ва } = а -
Левосторонняя и правосторонняя критические границы одного и того же уровня а связаны между собой соотношением
Ка = В1а . (3.53)
Двусторонними критическими границами уровня а случайной величины X называются такие числа В а, В а, что
Рх(Ва) = аа- рх(Ва) = 1 (3.54)
т. е. P{X Ва } = P{X S Ва } = ^
Между односторонними и двусторонними критическими границами случайной величины X существуют следующие соотношения
Ва = К = Вл ; Ва = Кл = В . (3.55)
/ 2 1а / 2 1а / 2 а / 2
Для стандартного нормального распределения N(0; 1) двусторонние критические границы уровня а симметричны и имеют специальные обозначения Ва = иа, Ва = иа, при этом
Ф0(иа) = . (3.56)
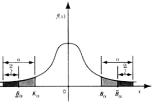
На рис. 3.3 указаны левосторонняя, правосторонняя и двусторонние критические границы для некоторого распределения.
249. Доказать формулы (3.35) - (3.39).
250. Случайная величина X имеет производящую функцию тх (t) = 0,2 +
+0,3et + 0,1e2t + 0,4e4t. Составить ряд распределения этой случайной величины,
найти её математическое ожидание и дисперсию, а также производящую функ-
2
цию случайной величины Y = X .
251. Найти производящую функцию случайной величины, заданной рядом распределения
252. Доказать формулу (3.41).
253. Доказать свойства производящей функции (3.42) - (3.43).
254. Найти производящую функцию случайной величины, распределённой по нормальному закону.
1 lxa\2
га
Решение. mX (t) = MetX = f
X yj2na J
etxe 2( a ) dx =
ra
- + a2t2
ea+ 2 dx =
ra 1 -2
ra 1 ( 2 2 , Д 2 2 2, 2 2, 4,2 4,2)
~--2\x 2x(aa t)a 2aa t2aa ta t a t ) 1 1
e 2a2 dx = , I
yj2na J
xaa t
"TLX
f
In a J
V2n
ra
ra
2,2 . a t
at --
= e 2
+ a2t2 dx = ea + 2
2,2
a t
2,2
a c
ra 1
e~ 2
xaa t
raaa t
f
In a J
at
at+
V2n
| X | 1 | 0 | 1 |
| p | 0,2 | 0,3 | 0,5 |
255. Найти четвёртый начальный момент случайной величины X N(0; 1).
2,2 12
t t
at
РЕШЕНИЕ. Производящая функция mx (t) = e
2 = e 2 , её производные \e 2 ) = te 2 ,
t2 It2 ^(3)
| t2 (t2 ^(4) | ||||||
| (4) |
|
t=0 = 3. ? |
e 2 / = e 2 12e 2 , \e 2 / = 3te 2 13e 2 , \e 2 / = 3e 2 6t2e 2 14e 2 , поэтому четвёртый начальный момент v^(X) = \e 2
256. Найти производящую функцию и с её помощью вычислить математическое ожидание для случайной величины X G(p).
257. Найти производящую функцию для случайной величины X ~ R(a; b).
258. Найти производящую функцию, второй начальный и третий центральный моменты для случайной величины X ~ Ехр(д).
259. Доказать, что величина M(X c) достигает своего наименьшего значения при c = MX.
260. Найти моду и медиану случайной величины X ~ R(a; b).
261. Найти моду и медиану случайной величины X ~ Ехр(д).
262. Пусть X некоторая случайная величина, Y = aX b (a и b неслу
Ax , a 0,
чайные постоянные, a ^ 0). Доказать, что Ay =
X-
0/ Y
263. Пусть X некоторая случайная величина, X = XMX. Доказать, что
264. Найти коэффициент асимметрии и эксцесс случайной величины
X ~ N (a; a).
265. Найти коэффициент асимметрии и эксцесс случайной величины X - П(А).
266. Найти коэффициент асимметрии и эксцесс случайной величины X - R(a; b).
267. Найти коэффициент асимметрии и эксцесс случайной величины X, имеющей распределение Лапласа с плотностью f (x) = -2e~^xI, x g R .
268. Найти для случайной величины X N(0; 1): а) 2,5%-ную и 97,5%-ную квантили ; б) 5%-ную правостороннюю критическую точку.
2
269. Найти 5%-ную и 95%-ную квантили распределений: а) T^; б) Х20.
270. Найти 5%-ную и 95%-ную квантили распределения Б^.
§3.5. Многомерные случайные величины
Многомерная случайная величина X = (Хг, X2,..., Xn) это совокупность случайных величин Хг (г = 1,2,..., n), заданных на одном и том же вероятностном пространстве П.
Закон распределения вероятностей многомерной случайной величины задаётся её функцией распределения
FX(x 1, x 2,'., xn) = FXi X2 у-Xn (x 1, Х 2,', Xn) = (X1 x 1) П (X2 x 2) П П (Xn xn)},
которая является числовой функцией многих переменных и (как вероятность) принимает значения на отрезке [0; 1].
Функция распределения многомерной случайной величины обладает следующими свойствами.
(3.57)
(3.58)
(3.59)
(3.60)
(3.61)
для всех x 1, x2, , xn g Ж : 0 ^ Fx x x (x 1, x2, - - - , xn) ^ 1;
Fx X X (xл, x2, , xn) не убывает по каждому аргументу; Х1Х 2 ,',Xn 1 2
Fx x x (xл, x2, , xn) непрерывна слева по каждому аргументу;
Х1Х 2 ,'Xn 1 2
FX1,X2,,Xn (x1, x2, - , xn-1,-те) = 0;
FX1 ,X2 ,y,Xn (x 1,x2, - , xn-1, +^) = FX1 ,X2 ,y,Xn-1 (x 1,x2, ^, xn-1)
В отличие от одномерного случая, выполнение свойств (3.57) - (3.61) для некоторой функции F : Жп ^ Ж не гарантирует, что эта функция является функцией распределения некоторой многомерной случайной величины.
Многомерные случайные величины, так же, как и одномерные, могут быть дискретными (когда наборы возможных значений образуют конечное или счётное множество) или непрерывными (когда множество наборов возможных значений несчётно).
Всюду ниже в данном параграфе будут рассматриваться двумерные случайные величины.
Вероятность попадания двумерной случайной величины в полуоткрытый прямоугольник равна
(3.62)
неотрица-
P((a1 ^Х1 b1) П (a2 ^Х1 bj)} =
= FX1 ,Х2 (b1, b2) - FX1 ,X2 (a1, b2) - FX1 ,X2 (b1,a2) + FX1 ,X2 (a1,a2)
Если дополнительно к условиям (3.57) - (3.61) потребовать от функции F : тельности величины
FX1 ,Х2 (b1, b2) - FX1 ,Х2 (a1, b2) - FX1 ,Х2 (b1,a2) + FX1 ,Х2 (a 1,a2)
для любых a^,a^,2 ? Ж таких, что b^ ^ а^, 2 ^ а2 то тогда эта функция обязательно будет
являться функцией распределения некоторой двумерной случайной величины.
Двумерные дискретные случайные величины удобно задавать с помощью таблиц распределения
| \х y\ |
x 1 | x2 | xn |
| у1 | P11 | P12 - | - P1n - |
| у 2 | P21 | P22 ' | - P2n |
| ут | Pm 1 | Pm 2 | pmn |
соответствуют всем возможным значениям первой
В такой таблице заголовки столбцов xj
компоненты X, а названия строк уг всем возможным значениям второй компоненты Y. При этом в клетку, находящуюся в i -й строке и в j -м столбце, записывается значение вероятности Pj = P{(X = xj) П (Y = уг)}. Естественно,
ЕЕ?, = i- (3-64)
г j
Функция распределения двумерной дискретной случайной величины равна