Колемаев В. - Теория вероятностей в примерах и задачах
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ ИНСТИТУТ ИНФОРМАЦИОННЫХ СИСТЕМ УПРАВЛЕНИЯ
Предисловие
Предлагаемое учебное пособие предназначено для студентов экономических специальностей высших учебных заведений, изучающих курс теории вероятностей и математической статистики. В пособии представлены задачи, которые служат для усвоения материала всех разделов теории вероятностей на конкретных примерах, возникающих в практике управления экономическими, социальными и финансовыми системами.
В процессе решения таких задач студент не только закрепляет и углубляет теоретические знания, полученные на лекциях, но и учится применять эти знания при постановке и решении реальных экономических задач. В предлагаемом пособии экономические, финансовые и социологические приложения методов теории вероятностей и математической статистики выходят на первый план, серьёзный акцент делается не только на методы решения задач, но и на построение математических моделей, анализ и экономическую интерпретацию полученных результатов.
В результате использования учебного пособия студент знакомится с основными проблемами управления, экономики, финансов, социологии и других смежных областей, при решении которых полезно применение вероятностно-статистических методов, учится ориентироваться в математических методах и по экономической постановке задачи определять, в каком разделе математики искать средства для её решения, переходить от экономической постановки задачи к её математической модели, проводить по этой модели расчёты и получать числовые результаты, анализировать эти результаты и делать количественные и качественные выводы, необходимые для принятия решений в своей предметной области.
Учебное пособие отражает опыт преподавания теории вероятностей и математической статистики в Государственном университете управления (см. [1], [8], [9], [10], [11], [14], [20], [21], [23]) и полностью соответствует учебнику [1].
Задачи разбиты по главам и параграфам в соответствии со структурой действующих учебных программ и учебника [1]. В каждом параграфе предлагаются необходимые теоретические сведения, задачи с решениями, а также большое число задач для самостоятельной работы, сопровождающихся ответами.
В решениях задач большое внимание уделяется не только методам и алгоритмам, но и переходу от экономической постановки проблемы к математической модели, экономическому анализу полученных результатов. Внутри параграфов сложность возрастает от простых задач, для решения которых необходимо использовать стандартные формулы и приёмы, до довольно сложных, рассчитанных на студентов, изучающих расширенный курс теории вероятностей и математической статистики, решения этих задач содержат принципиально важные идеи либо требуют аккуратного проведения достаточно больших математических выкладок.
Чтобы облегчить студентам освоение сложной дисциплины, авторы стремились сделать задачи интересными и по форме, и по содержанию.
При подготовке пособия авторами был учтён опыт всех известных им задачников по теории вероятностей и математической статистике. Ряд задач заимствован из работ [1]-[25].
Большинство задач являются оригинальными и подготовлены авторами специально для данного издания.
Работа авторов над пособием распределилась следующим образом: предисловие и теоретические введения к параграфам написаны совместно д-ром экон. наук, проф. В. А. Колемаевым, канд. техн. наук, проф. В. Н. Калининой и канд. экон. наук В. И. Соловьёвым; задачи 13-18, 25-27, 39, 40, 51, 53, 72-75, 77, 90, 101, 103, 104, 106, 110-112, 139-143, 147, 148, 154-157, 170, 175, 176, 193, 198, 200, 201, 213, 224, 231, 232, 234, 247-249, 252, 253, 256, 260, 261, 264-267, 271, 272, 275, 283, 284, 301, 304, 309, 310, 314, 315, 317, 319, 321323, 330, 343, 348, 358-360 (всего 83 задачи) предложены д-ром экон. наук, проф. В. А. Колемаевым, задачи 64-66, 70, 82, 83, 121, 122, 130, 158, 167, 168, 172, 179, 182-184, 189, 191, 199, 207, 225-229, 244-246, 255, 262263, 268-270, 294, 296-299, 311, 316, 324, 351 (всего 44 задачи) предложены канд. техн. наук, проф.
В. Н. Калининой, задачи 1-12, 19-24, 28-37, 41-46, 48, 52, 55, 57-63, 69, 71, 78-80, 84-88, 91-100, 102, 108, 109, 114-120, 123, 127-129, 131, 135-138, 146, 149-153, 159-160, 162, 165, 166, 169, 171, 174, 177, 178, 180, 185-188, 190, 192, 196, 197, 202, 204-206, 212, 214-216, 222, 223, 230, 235, 236, 239-243, 251, 254, 257-259, 273, 274, 276-282, 285-293, 295, 300, 302, 303, 305-308, 312, 313, 318, 320, 325-329, 331-342, 344-347, 352-357, 361-369 (всего 200 задач) предложены канд. экон. наук В. И. Соловьёвым, задачи 38, 47, 54, 56, 67, 68, 81, 89, 105, 107, 132-134, 144, 145, 161, 163, 164, 173, 181, 194, 203, 208-210, 217-220, 233, 250, 349, 350 (всего 33 задачи) предложены д-ром физ.-мат. наук, проф. В. И. Малыхиным, задачи 49, 50, 113, 126, 195, 211, 221, 237, 238 (всего 9 задач) предложены канд. техн. наук, доц.
А. П. Курочкиным; решения всех задач, ответы и приложения подготовлены канд. экон. наук В. И. Соловьёвым.
Глава 1. Вероятностные пространства
§1.1. Элементы комбинаторики
В теории вероятностей часто приходится иметь дело с задачами, в которых необходимо подсчитывать число возможных способов совершения каких-либо действий. Задачи такого типа называются комбинаторными, а раздел математики, занимающийся решением таких задач, комбинаторикой.
Сформулируем два универсальных правила, применяемых при решении комбинаторных задач.
Правило произведения. Пусть требуется выполнить одно за другим какие-либо m действий.
Если первое действие можно выполнить способами, второе действие - n2 способами и так до m -го действияя, которое можно выполнить nm способами, то все m действий могут быть выполнены nn ¦¦¦nm способами.
Правило суммы. Пусть требуется выполнить одно из каких-либо m действий, взаимно исключающих друг друга.
Если первое действие можно выполнить n^ способами, второе действие - n2 способами и так до m -го действия, которое можно выполнить nm способами, то выполнить одно из этих m действий можно (n^ + n2 + + nm) способами.
Напомним понятие факториала, активно используемое в комбинаторике. Факториалом натурального числа n называется число
n! = n(n l)(n 2) 3 - 2 - 1. (1.1)
По определению, факториалом нуля является единица:
0! = 1. (1.2)
Рассмотрим некоторое множество S, состоящее из n различных элементов. Пусть 1 ^ k ^ n. Назовём множество, состоящее из k элементов, упорядоченным, если каждому элементу этого множества поставлено в соответствие число от 1 до k, причём различным элементам множества соответствуют разные числа.
Размещениями из n элементов по k называются упорядоченные подмножества множества S, состоящие из k различных элементов и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений из n элементов по k равно
An = ( П ПІ = n(n 1)(n 2)'(n k + 1). (13)
(n k)!
Перестановками из n элементов называются размещения из n элементов по n, т. е. упорядоченные подмножества множества S, состоящие из всех элементов данного множества и отличающиеся друг от друга только порядком их расположения.
Число перестановок из n элементов равно
Сочетаниями из n элементов по k называются подмножества множества S, состоящие из k различных элементов и отличающиеся друг от друга только составом элементов.
Число сочетаний из n элементов по k равно
Размещениями с повторениями из n элементов по k называются упорядоченные подмножества множества S, состоящие из k элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга составом элементов или порядком их расположения.
Число размещений с повторениями из n элементов по k равно
A n =nk. м
Сочетаниями с повторениями из n элементов по к называются подмножества множества S, состоящие из к элементов, среди которых могут оказаться одинаковые, и отличающиеся друг от друга только составом элементов.
Число сочетаний с повторениями из n элементов по к равно
Cк = Ck = (п + к - 1)! = (п + к - 1)(n + к - 2) - - - n
п n+h-1 к !(n -1)! к(к - 1)(к - 2)--- 3 - 2 - 1 (1 7)
Отметим, что формулы (1.4) - (1.7) сохраняют смысл и остаются справедливыми и при к = 0 . Если во множестве S, состоящем из n элементов, есть только m различных элементов, то перестановками с повторениями из n элементов называются упорядоченные подмножества множества S, в которые первый элемент множества S входит n^ раз, второй элемент n2 раз и так до
m -го элемента, который входит nm раз (^ + n^ +-----+ nm = n).
Число перестановок с повторениями из n элементов, в которые первый элемент множества S входит n1 раз, второй элемент n2 раз и так до m -го элемента, который входит nm раз
(n1 + n2 + + nm = n), равно
Pn(n1,
(1.8)
n 2, ¦¦¦, nm) =
1. Маша поссорилась с Петей и не хочет ехать с ним в одном автобусе. От общежития до института с 7 до 8 ч отправляется пять автобусов. Не успевший на последний из этих автобусов опаздывает на лекцию.
Сколькими способами Маша и Петя могут доехать до института в разных автобусах и не опоздать на лекцию?
РЕШЕНИЕ. Петя может доехать до института n1= 5 различными способами (на одном из пяти
автобусов), при этом Маше остаётся только ^ = 4 способа (так как один из автобусов занят Петей). Таким образом, по правилу произведения у Пети и Маши есть = 5 - 4 = 20 различных способов добраться до института в разных автобусах и не опоздать на лекцию. ?
2. В информационно-технологическом управлении банка работают три аналитика, десять программистов и 20 инженеров. Для сверхурочной работы в праздничный день начальник управления должен выделить одного сотрудника.
Сколько способов существует у начальника управления?
РЕШЕНИЕ. Начальник управления может отобрать одного аналитика ^ = 3 способами, одного
программиста ^ = 10 способами, а одного инженера n3 = 20 способами. Поскольку по условию задачи начальник управления может выделить любого из своих сотрудников, согласно правилу суммы у него существует ^ + n2 + Пз = 3 + 10 + 20 = 33 различных способа выбрать сотрудника для сверхурочной работы. ?
3. Начальник службы безопасности банка должен ежедневно расставлять десять охранников по десяти постам. В целях усиления безопасности одна и та же комбинация расстановки охранников по постам не может повторяться чаще одного раза в месяц.
Чтобы оценить, возможно ли это, найти число различных комбинаций расстановки охранников.
РЕШЕНИЕ. Первый способ. На первый пост начальник службы безопасности может назначить любого из n1 = 10 охранников, на второй пост любого из оставшихся ^ = 9 охранников и так
до девятого поста, на который можно назначить любого из оставшихся ^ = 2 охранников, при этом оставшийся n^ = 1 охранник будет назначен на десятый пост. Поэтому, согласно правилу произведения, у начальника службы безопасности есть n^2 - - - Пщ = 10 - 9 2 - 1 = 10! = 3 628 800
способов расстановки охранников по постам. Поскольку количество дней в месяце не превышает 31, у начальника службы безопасности заведомо существует достаточное число способов расстановки своих подчинённых по постам.
Второй способ. Число способов расстановки десяти охранников по десяти постам, существующих у начальника службы безопасности, описывается числом перестановок из 10 элементов, т. е. P10 = 10! = 3 628 800 . ?
4. Определить, сколькими способами можно разместить на шахматной доске восемь ладей так, чтобы они не били друг друга.
5. Новый президент банка должен назначить двух новых вице-президентов из числа десяти директоров. Сколько способов существует у президента, если:
а) один из вице-президентов (первый) выше другого по должности; б) вицепрезиденты по должности равны между собой.
РЕШЕНИЕ. Первый способ. а) Первого вице-президента можно выбрать из Пі = 10 претендентов, при этом на пост второго вице-президента будут претендовать n^ = 9 оставшихся директоров. Поэтому, согласно правилу произведения, у нового президента банка есть = 10 - 9 = 90
способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров. б) Пусть первое действие заключается в том, что президент отбирает двух человек на должности вице-президентов, а второе действие в том, что президент говорит отобранным людям, кто из них является первым вице-президентом, а кто вторым. Пусть первое действие можно выполнить n1 способами, второе действие, очевидно, можно выполнить n2 = 2 способами, и по правилу произведения число способов назначения двух вице-президентов, один из которых подчиняется другому, из числа десяти директоров составляет n^n^ = 2^ .
6. В кредитном отделе банка работают восемь человек. Сколько существует способов распределить между ними три премии: а) одинакового размера; б) разных размеров, известных заранее?
7. Одна из воюющих сторон захватила в плен 12 солдат, а другая 15. Определить, сколькими способами стороны могут обменять семерых военнопленных.
8. Петя и Маша коллекционируют видеокассеты. У Пети есть 30 комедий, 80 боевиков и 7 мелодрам, у Маши 20 комедий, 5 боевиков и 90 мелодрам.
Сколькими способами Петя и Маша могут обменяться тремя комедиями, двумя боевиками и одной мелодрамой?
9. В сессию в течение 20 дней студенты одной группы должны сдать пять экзаменов. Сколькими способами можно составить расписание экзаменов, если:
а) запрещается сдавать два экзамена в один день; б) между двумя экзаменами должен пройти хотя бы один день для подготовки?
10. В банке девять учредителей.
Регистрационные документы хранятся в сейфе. Сколько замков должен иметь сейф, и сколько ключей к ним нужно изготовить, чтобы доступ к содержимому сейфа был возможен только тогда, когда соберётся не менее шести учредителей?
11. Маша решила помириться с Петей и позвонить ему, но забыла две последних цифры его телефона и набирает их наудачу.
Найти наибольшее возможное число неудачных попыток, которые сделает Маша, прежде чем дозвонится до Пети.
12. Сколько автомобилей в одном городе можно обеспечить государственны
ми регистрационными знаками, если каждый регистрационный знак состоит из кода города, трёх букв, имеющих одинаковое начертание как в русском, так и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х), и
трёх цифр?
13. Доказать правило произведения.
14. Доказать правило суммы.
15. Доказать справедливость формул (1.3) - (1.5).
16. Доказать равенство: сП = сП-к (0 ^ к ^ п).
= сП-к. ?
Решение. сП = П = ---тп.--т-
к!(п-к)! (п-к) ![п-(п-к)]!
17. Равенство Паскаля.
Доказать равенство: сП + сП+1=сП+1 (0 ^ кп).
18. Доказать равенство: с + с1 + с^ +-----+ сП = 2П.
19. Определить, сколько существует вариантов опроса группы из десяти студентов на одном занятии по теории вероятностей, если ни один из студентов не будет подвергнут опросу дважды, и на занятии может быть опрошено любое число студентов (в том числе, ни один)?
20. Доказать равенство: (сП )2 + (сП )2 + (с2 )2 +-----+ (сП )2 = с2П.
21. Маша очень любит пирожные и ежедневно в булочной рядом с институтом покупает шесть пирожных (одинаковых или разных). Всего в булочной продаётся 11 сортов пирожных.
Сколькими способами Маша может выбрать из них шесть штук?
РЕШЕНИЕ. Каждому набору пирожных, которые выберет Маша, будем ставить в соответствие последовательность нулей и единиц, определяемую по следующему правилу. Напишем подряд столько единиц, сколько пирожных первого вида выбрала Маша, далее поставим нуль и после него запишем количество отобранных пирожных второго вида и т. д. Например, комбинации одно пирожное второго вида, три пирожных пятого вида и одно пирожное восьмого вида соответствует такая последовательность: 010001110001000 (нули отделяют виды пирожных друг от друга, поэтому нуль после одиннадцатого вида не нужен).
При этом каждому набору пирожных взаимно однозначным образом соответствует последовательность, построенная по описанному правилу. Все такие последовательности состоят, очевидно, из 16 знаков, причём 10 из них нули, которые могут занимать любое место. Поэтому количество способов выбора пирожных равно количеству
всех таких последовательностей, т. е. числу размещений десяти нулей по 16 местам: с}0 = 8 008. ?
22. В конкурсе по трём номинациям участвуют десять кинофильмов.
Вычислить число вариантов распределения призов, если по каждой номинации установлены: а) различные призы; б) одинаковые призы.
23. Сколько различных слов можно составить, переставляя буквы в слове мама?
Выписать все эти слова.
РЕШЕНИЕ. Число различных слов, которые можно составить, переставляя буквы в слове мама, описывается числом перестановок с повторениями из п = 4 элементов (букв в слове мама), в которые первый элемент (буква м) входит П1 = 2 раза, а второй элемент (буква а) П2 = 2 раза
~ 4!
(П1 + п2 = 4 = п). Это число равно P4(2,2) = удд = 6 . Шесть различных слов, получающиеся перестановками букв в слове мама, таковы: ммаа, мама, маам, амма, амам, аамм. ?
24. Сколько различных слов можно составить, переставляя буквы в слове математика?
25. Доказать справедливость формул (1.6) - (1.8).
§1.2. Исчисление событий
Случайное событие A, связанное с опытом S, это такое событие, которое может произойти или не произойти в результате опыта S, причём заранее, до проведения опыта, неизвестно, произойдёт оно или нет. Всюду в дальнейшем при рассмотрении случайных событий мы будем опускать слово случайное. Достоверным событием, связанным с опытом S, называется такое событие О, которое обязательно произойдёт в результате опыта S . Невозможным событием, связанным с опытом S, называется такое событие 0, которое обязательно не произойдёт в результате опыта S .
Над событиями A и B, связанными с одним и тем же опытом S, определены следующие операции.
Событие A влечёт за собой событие B (или событие A вложено в событие B), если каждое появление события A сопровождается появлением события B . Это обозначается как A С B . События A и B называют эквивалентными, если A С B и B С A . Эквивалентность обозначается как A = B.
Объединением (или суммой) событий A и B называется событие A U B (или A + B), которое наступает всегда, когда наступает либо событие A, либо событие B.
Пересечением (или произведением) событий A и B называется событие A П B (или AB), которое наступает всегда, когда события A и B наступают одновременно.
Дополнением события B до события A (или разностью событий A и B) называется событие A \ B, которое наступает всегда, когда наступает событие A, и при этом не наступает событие B.
Противоположным событию A называется событие A = О \ A (читается не A ), которое наступает всегда, когда событие A не наступает.
События A и B называются несовместными, если A П B = 0, т. е. если в результате опыта события A и B не могут наступить одновременно.
Говорят, что события ЯрH2,Hn образуют полную группу, если они попарно несовместны (Нг П Н^ = 0, i ^ j) и их объединение эквивалентно достоверному событию (Я^ U Я^ U U - - - U Нп = О).
Случайное событие ш, связанное с опытом S, которое невозможно представить как объединение или пересечение более простых событий, связанных с тем же опытом, называется элементарным событием. Очевидно, достоверное событие О = {ш} это множество всех элементарных событий (поэтому О называют ещё пространством элементарных событий), а невозможное событие 0 это пустое множество.
Любое событие, связанное с опытом S, можно представить как некоторое подмножество достоверного события О , т. е. как множество некоторых элементарных событий.
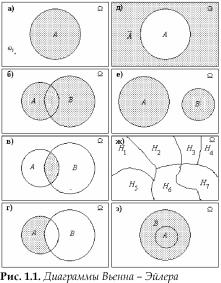
Для наглядного представления событий, операций над событиями и отношений между ними используются диаграммы Вьенна - Эйлера (рис. 1.1). На этих диаграммах достоверное событие О изображается в виде некоторой области на плоскости, элементарные события точками внутри области, соответствующей О. При этом любому случайному событию A будет соответствовать некоторая геометрическая фигура внутри области, соответствующей О (рис.
1.1а). Объединение A U B событий A и B состоит из всех элементарных событий, принадлежащих, по крайней мере, одному из событий A и B (рис. 1.1б).
Пересечение A П B событий A и B состоит из всех элементарных событий, принадлежащих одновременно обоим событиям A и B (рис. 1.1в). Дополнение A \ B события B до события A состоит из всех элементарных событий, принадлежащих событию A и при этом не принадлежащих событию B (рис.
1.1г). Событие A, противоположное событию A, состоит из всех элементарных событий, не принадлежащих событию A (рис. 1.1д). Несовместные события не имеют общих элементарных событий (рис.
1.1е). Полная группа событий представлена на рис.
1.1ж. Событие A влечёт за собой событие B, если все элементарные события, входящие в A, входят и в B (рис.
1.1з).
Операции над событиями обладают следующими свойствами:
коммутативность объединения событий:
| A U B = B U A , | (1.9) |
| ассоциативность объединения событий: | |
| (A U B) U C = A U (B U C), | (1.10) |
| A U A = A, | (1.11) |
| A U A = О, | (1.12) |
| AU0 = A, | (1.13) |
| A UO = О, | (1.14) |
| коммутативность пересечения событий: | |
| A П B = B П A, | (1.15) |
| ассоциативность пересечения событий: | |
| (A П B) П C = A П (B П C), | (1.16) |
| дистрибутивность пересечения событий относительно объединения: | |
| (A U B) П C = (A П C) U (B П C), | (1.17) |
| A П A = A, | (1.18) |
| A П A = 0, | (1.19) |
| AП0 = 0, | (1.20) |
| AПО = A, | (1.21) |
| A \ B = A П B, | (1.22) |
| О = 0, | (1.23) |
| 0 = О / |
(1.24) |
| правила де Моргана: | |
| A U B = A П B, | (1.25) |
| A П B = A U B. | (1.26) |
27. Привести примеры несовместных случайных событий.
28. Известно, что A С B. Найти: а) A U B; б) A П B.
| Рис. 1.2. События AUB (а) и AnB (б), когда ACB |
рис. 1.2а, событие A П B на рис. 1.2б, откуда следует, очевидно, что AUB = B, AnB =A. ?
29. Установить, при каких условиях события A и A П B являются эквивалентными.
30. Пусть A, B, C произвольные события. Найти выражения для событий,
состоящих в том, что: а) произошло только A; б) произошли A и B, но C не произошло; в) все три события произошли; г) произошло хотя бы одно из этих событий; д) произошло хотя бы два события; е) ни одно из событий A, B и C не произошло; ж) произошло не более двух из событий A , B и C ; з) произошло ровно одно из этих событий; и) произошло ровно два из этих событий.
31. Пусть A, B, C некоторые события, причём A С B. С помощью диаграмм Вьенна - Эйлера упростить выражения: а) A П B; б) A U B; в) A П B П C; г) A U B U C.
32. Проверить справедливость следующих утверждений, сравнивая диаграммы Вьенна - Эйлера для событий, стоящих в левых и в правых частях: а) (AUB)\C = AU(B\C); б) A П B П C = A П B П (C U B); в) AUBUC = Au(B\(AnB))U
U(C\(AnC)); г) A U B = (A\(A П B)) U B; д) (A U B)\A = B; е) (A U B U C) = AПBПО;
ж) (BUBnC = (AПC)U(BПC); з) (AUB) ПC = AПBПC; и) (AUB)nC ^(^(AUB^;
к) A П B ПC С (B ПC) U (C П A); л) (A^) U (BHC) U (CПA)СA U B UC; м) AпBпC С AUB.
33. С помощью диаграмм Вьенна - Эйлера убедиться в справедливости свойств (1.9) - (1.26) для произвольных событий A, B, C.
34. Проверить, являются ли события A и A U B (где A и B произвольные события) несовместными.