Формулы и схемы из функциональных элементов
Тогда если все кривые, сопоставленные ребрам графа, не имеют общих точек, кроме концевых, то это множество точек и кривых называется геометрической реализацией графа G.
Теорема 3.1. Каждый конечный граф G можно реализовать в трехмерном евклидовом пространстве (без пересечения ребер).
Доказательство. Возьмем в пространстве любую прямую I и разместим на ней все вершины графа G. Пусть в G имеется q ребер.
Проведем q полуплоскостей через I так, чтобы прямая I была их общим ребром (типа тетрадки). После этого каждое ребро графа G можно изобразить линией в своей полуплоскости и они, очевидно, не будут пересекаться.
Определение. Граф называется планарным, если существует его планарная реализация, то есть геометрическая реализация на плоскости (без пересечения ребер).
Если имеется планарная реализация графа на плоскости и мы разрежем плоскость по всем линиям этой планарной реализации, то плоскость распадется на части, которые называются гранями этой планарной реализации (одна из граней бесконечна, она называется внешней гранью).
Теорема 3.2 (формула Эйлера.) Для любой планарной реализации связного планарного графа G = (V, Е) с р вершинами, q ребрами и г гранями выполняется равенство: р q + г = 2.
Доказательство. При фиксированном р индукцией по q. Так как G связный граф, то qp 1 по следствию из леммы 1.4.
а) Базис индукции: q = р 1. Так как G связных! и q = р 1, то по теореме 2.3 G дерево, то есть в G нет циклов. Тогда г = 1. Отсюда р q + г = р (р 1) + 1 = 2.
б) Пусть для р 1 g до теорема справедлива. Докажем, что для g = go она тоже справедлива. Пусть G связный граф с р вершинами и до ребрами и пусть в его планарной реализации г граней. Так как до р 1, то G не дерево.
Следовательно, в G есть цикл. Пусть ребро е входит в цикл. Тогда к нему с двух сторон примыкают разные грани. Удалим ребро е из G. Тогда две грани сольются в одну, а полученный граф G\ по лемме 1.3 останется связным.
При этом получится планарная реализация графа G\ с р вершинами, до 1 ребрами и г-1 гранями. Так как до 1 до, то, по предположению индукции, для G\ справедлива формула Эйлера, то есть р (до 1) + (г 1) = 2, откуда р до + г = 2. Что и требовалось доказать.
Следствие 1. Формула Эйлера справедлива и для геометрической реализации связных графов на сфере.
Доказательство. Пусть связный граф Сер вершинами и g ребрами реализован на сфере S так, что число граней равно г. Пусть точка А на сфере не лежит на линиях этой геометрической реализации. Пусть Р некоторая плоскость.
Поставим сферу S на Р так, чтобы точка А была самой удаленной от плоскости. Спроектируем S на Р центральным проектированием е центром в А. Тогда на плоскости Р мы получим геометрическую реализацию связного графа с р вершинами и g ребрами, причем число граней будет равно г (грань на сфере, содержащая А, отображается во внешнюю грань на плоскости). По теореме 3.2 получаем р q + г = 2.
Следствие 2. Для любого выпуклого многогранника справедливо равенство р q + г = 2, где р число вершин, q число ребер, г число граней.
Доказательство. Пусть выпуклый многогранник М имеет р вершин, g ребер и г граней.
Пусть О внутренняя точка многогранника М. Рассмотрим сферу S с центром в О настолько большого радиуса, чтобы М целиком лежал внутри S. Рассмотрим центральное проектирование с центром в точке О, и спроектируем вершины и ребра М на S. Тогда на S мы получим геометрическую реализацию некоторого связного графа с р вершинами, g ребрами и г гранями. Отсюда р q + г = 2.
Формула Эйлера позволяет доказать непланарность некоторых графов.
Определение. Графом называется граф с 5 вершинами, в котором каждая пара вершин соединена ребром (см. рис.
3.1).
Теорема 3.3. Граф не планарен.
Доказательство. Допустим, что для графа А5 существует планарная реализация. Так как граф А5 связен, то для этой планарной реализации справедлива формула Эйлера р q + г = 2. Поскольку в графе А5 имеем р = 5 и g = 10, то число всех граней должно
равняться г = 2 р + q = 7. Пусть грани занумерованы 1.2.....г
и пусть при обходе г-ой грани по периметру (по ее краю) проходится д* ребер. Так как при этом каждое ребро проходится дважды (оно является стороной для двух граней), то Е/=і Ц = 2g = 20.
Но в каждой грани не менее 3 сторон. Поэтому д/3 для всех і. Отсюда Е/=і g/3r = 21.
Получаем 2021 противоречие. Значит для графа ІД не существует планарной реализации.

Рис. 3.1.
Определение. Графом А33 называется граф с 6 вершинами щ, в2, аз, 61,625^3, в котором каждая вершина щ соединена ребром с каждой вершиной bj и нет других ребер (см. рис.
3.1).
С графом А33 связана следующая известная задача о трех домах и трех колодцах. Есть 3 дома и 3 колодца, но хозяева домов в большой вражде.
Можно ли так проложить дорожки от каждого дома к каждому колодцу, чтобы они нигде не пересекались?
Ответ на этот вопрос дает следующая теорема.
Теорема 3.4. Граф A3 3 не планарен.
Доказательство. Допустим, что для графа A3 3 существует планарная реализация. Так как граф A3 3 связен, то для этой планарной реализации справедлива формула Эйлера р q + г = 2. Поскольку в графе АДз имеем р = 6 и q = 9, то число всех граней должно равняться г = 2р + д = 5. Так же, как в доказательстве предыдущей теоремы, получаем, что ЕДі Щ = 2g = 18, где д?; число сторон в г-ой грани. Но в графе A3 3 нет циклов длины 3. Поэтому в каждой грани не менее 4 сторон.
Следовательно, д/4 для всех і. Отсюда Е/=і g/4r = 20. Получаем 1820 противоречие.
Значит для графа A3 3 не существует планарной реализации.
Граница любой грани является путем в графе, так, например, границей внутренней грани на рис. 3.2 является путь (указаны только вершины): 1,2,4,5,4,6,4,2,3,1. Пусть длина границы г-ой грани (число
ребер) равна g* (для грани на рис. 3.2 g = 9).
2
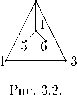
Лемма 3.1. Для любой геометрической реализации на плоскости связного планарного графа с q ребрами выполняется равенство:
t Чі = 2g,
І= 1
где суммирование ведется по всем граням (включая внешнюю гранъ).
Доказательство. Равенство следует из того, что у каждого ребра две стороны и при суммировании д,; каждое ребро учитывается дважды: либо оно входит в границы двух соседних граней, либо оно дважды учитывается в одной грани.
Теорема 3.5. Если в связном планарном графе G = (V, Е) с р верш,инами и q ребрами нет циклов длины меньше к (кЗ), то g^4j(p 2).
Доказательство. Так как по условию дД для всех к, то из леммы 3.1 получаем 2qkr и Гу.
Из формулы Эйлера г = 2 р + д. Отсюда 2 - Р + gf¦ Далее (к - 2)qk(p - 2) и q^(p - 2).
Следствие 1. Для любого связного планарного графа G = (?,Е) без петель и кратных ребер с р верш,инами и q ребрами справедливо неравенство: q3(p 2).
Указание. В теореме 3.5 можно взять к = 3.
Следствие 2. Для любого планарного графа, G = (И, Е) без петель и кратных ребер с р вершинами, q ребрами и т связными компонентами справедливо неравенство: дЗ(р 2т).
Доказательство. Пусть в г-ой связной компоненте (г = 1,2,..., т) рі вершин и дг- ребер. Тогда в ней по следствию 1 д,;3(р,: 2).
Суммируя все эти неравенства, получаем дЗ(р 2т).
Следствие 3. В любом планарном графа, G = (И, Е) без петель и кратных ребер есть вершина степени не более 5.
Доказательство. Пусть G планарный граф е р вершинами и g ребрами.
Тогда дЗ(р 2) 3р. Пусть dmjn минимальная степень вершин в G. Тогда е учетом теоремы 1.1 получаем
р
6р 2g = Y) deg 'Щрдты.
І= 1
Отсюда dmin 6, то есть dmin5.
Если ребро графа изображено в виде линии, то можно на ней поставить точку и считать ее новой вершиной степени 2. Формально эта операция определяется следующим образом.
Определение. Пусть G любой граф и (а,Ь) его ребро.
Операцией подразделения ребра (а,Ь) называется удаление из графа G ребра (а, 6), добавление новой вершины с и добавление двух новых ребер (а, с) и (с, 6).
Определение. Граф G\ называется подразделением графа G, если G\ может быть получен из G несколькими подразделениями ребер.
Определение. Графы G\ и (Д называются гомеоморфнымщ если существуют их подразделения, которые изоморфны.
Существует следующий критерий планарности.
Теорема 3.6 (Понтрягина-Куратовекого). Для того, чтобы граф G был планарным, необходимо и достаточно, чтобы он не содержал ни одного подграфа, гомеоморфного графам К-, или 1Д:.
Доказательство. 1) Необходимость. Пусть G планарный.
Допустим, что он содержит подграф Gі, гомеоморфный графу К§ или ІГз 3. Рассмотрим планарную реализацию графа G. Удалив лишние вершины и ребра, мы получим планарную реализацию подграфа G\. Но G\ геометрически это граф К§ или ІГ3 3 с точками на ребрах.
Если проигнорировать эти точки, то мы получим планарную реализацию графа К§ или ІГ3 3. Но это невозможно по теоремам 3.3 и 3.4.
2) Достаточность доказывается тяжело, и здесь мы это доказательство опустим. Доказательство можно найти, например, в [2].
Подмножество вершин графа называется независимым^ если никакие вершины из этого подмножества не смежны (не соединены ребром). Во многих приложениях рассматриваются разбиения вершин на независимые подмножества.
Такие разбиения удобно описывать следующим образом.
Определение. Пусть К = {СД С2, ¦ ¦ ¦, Ст} произвольное множество элементов, называемых цветами.
Отображение С : V {СД С2, ¦ ¦ ¦, СД}, где V множество вершин графа G, называется раскраской (вершинной) графа G. Раскраска называется правильной, если для любого ребра (?щьД G Е выполняется С(?Д Д С(?ф).
Теорема 3.7. Вершины любого планарного графа можно правильно раскрасить в не более чем 5 цветов.
Доказательство (индукцией по числу вершин р).
1) Базис индукции: р = 1 очевидно.
2) Пусть для р Ро утверждение справедливо и пусть G = (V, Е) планарный граф с |П| = ро- По следствию 3 из теоремы 3.5 в С? есть вершина ? степени не более 5. Рассмотрим укладку на плоскости графа G без пересечения ребер. Удалим из G вершину ? и все инцидентные ей ребра.
Получим планарный граф G\ с числом вершин Ро 1. По предположению индукции его вершины можно правильно раскрасить в 5 цветов Сф С2, Сф Сф С§. Пусть в G вершина ? смежна с ?’і, т’2,... ,Vk, (где к5). Рассмотрим 2 варианта:
а) Среди цветов вершин Г|. с-..... гд. в G нет цвета С.) (1г5). Тогда вершине ? припишем цвет С{ и получим правильную раскраску графа G в 5 цветов.
б) Степень вершины ? равна 5 и среди вершин Г|. с-...., тд в G\ есть все 5 цветов. Без ограничения общности будем считать, что в укладке графа G ребра (и, гд), (?, тд), (?, ?д), (?, гц), (?, гд) выходят из ? в порядке по часовой стрелке и что С (и,) = С,, і = 1,..., 5. Пусть ?\ множество всех вершин в (?і, до которых можно дойти из ?\ по ребрам графа Gі, используя только вершины цветов С\ и С3. Возможны 2 варианта:
61) ед ^ ?\. Тогда в ?\ поменяем цвета С\ С3, С3 СТак как вершины из ?\ не смежны с другими вершинами цветов С\ и Сф то останется правильная раскраска и среди Г|. с-..... г?, не будет цвета С\.
Тогда вершине ? припишем цвет С\.
62) ?’з Е ?\. Это значит, что в G\ есть цепь из ?\ в тд, все вершины которой имеют цвета С\ и С3.
Эта цепь вместе с ребрами (т’з, ?) и (?,?і) образует цикл в G, причем вершины гд и тц лежат по разные стороны от этого цикла. Это значит, что из гд нельзя пройти в гд в графе G\ только по вершинам цветов и Сф Пусть 1 д множество всех вершин в Gі, до которых можно дойти из гд по ребрам графа Gі, используя только вершины цветов ('¦ и С\.
Тогда тд ^ Тд и далее поступаем как в 61).
В любом случае вершины графа G можно правильно раскрасить в не более чем 5 цветов, и теорема доказана.
Часть 2. Схемы
В настоящее время получили широкое распространение сложные преобразователи информации, которые составлены из простейших преобразователей (элементов) и в которых движутся сигналы нескольких типов, преобразуемые или передаваемые отдельными элементами в соответствии с определенными законами. В теории управляющих систем рассматриваются различные теоретико-графовые модели таких преобразователей, называемые схемами.
Каждая схема характеризуется структурой графом определенного вида и функционированием законом преобразования входных наборов или их последовательностей в выходные наборы или их последовательности. Функционирование схемы однозначно определяется ее структурой и функционированием элементов базиса набора простейших преобразователей, из которых построена схема.
При изучении схем решаются две основные задачи: задача анализа и задача синтеза. Задача анализа состоит в нахождении функционирования данной схемы, а задача синтеза в построении схемы, имеющей (реализующей) заданное функционирование.
Каждая из этих задач может рассматриваться либо как индивидуальная задача, и тогда ее решением является конкретное функционирование (схема), либо как массовая задача, и тогда ее решением должен быть алгоритм нахождения функционирования (схемы). Задача синтеза имеет, как правило, множество решений, из которых выбирают решение, оптимальное по какому-либо критерию.
Чаще всего в качестве такого критерия выступает сложность схемы, понимаемая как сумма сложностей составляющих ее элементов.
В §4-8 мы рассмотрим, как решается задача синтеза для некоторых конкретных видов схем.
§ 4. Формулы и схемы из функциональных элементов.
Задача синтеза и простейшие способы ее решения
В [8, с. 14-20] дано индуктивное определение формулы и реализуемой ею функции алгебры логики (ФАЛ). С содержательной точки зрения формула представляет собой слово, построенное из символов "базисных" ФАЛ, символов булевых переменных (БП) и разделителей, которое задает последовательность выполнения операций суперпозиции.
Напомним это определение и рассмотрим способ представления формул е помощью деревьев.
Пусть X счетный упорядоченный алфавит БП, и пусть у нас имеется счетный алфавит функциональных символов (ФС) для обозначения ФАЛ от этих БП. Две ФАЛ считаются, как обычно [8], равными, если они имеют одни и те же существенные БП и задают одинаковые отображения области значений этих БП, т. е. единичного куба Вп, где В = {0,1}, а п число БП, во множество В. Функция, существенно зависящая от всех своих БП, называется существенной.
Пусть, далее, Б = {гд. r~-j.....гд} система "исходных" ФАЛ
или, иначе, базис, где ФАЛ (pi, і = 1.....1. зависит от к,. /д 1. БП и
является существенной ФАЛ, если кі 2. Предполагается, что система базисных ФАЛ полна в алгебре логики, и допускается, в общем случае, наличие в ней "лишних" ФАЛ, после удаления которых оставшаяся система по-прежнему является полной (см. [8]). Предполагается также, что все ФС (fi, і = 1,..., Ь, различны, хотя, возможно, некоторым из них соответствуют равные ФАЛ.
Сопоставим каждому ФС pi, і = 1,... , Ь, функциональный элемент (ФЭ) Д, имеющий кі входов, причем входу с номером j соответствует j-я БП xj ФАЛ (fi, и один выход, на котором эта ФАЛ реализуется (см. рис. 4.1.а). Упрощенный вариант изображения ФЭ Д в виде вершины графа с пометкой рі, в которую входят кі упорядоченных, т. е. пронумерованных числами 1,.., к,, дуг, показан на рис.
4.1.6. При этом предполагается, что дуга с номером j, lj/д, соответствует j-му входу ФЭ €і. В дальнейшем мы, как правило, не будем делать существенных различий между ФС рі и ФЭ Si.
Чаще всего мы будем иметь дело с базисом Eq = {, V, і}, где базисными являются ФАЛ Хі ¦ Х-2, Х\ V Х’2 ш Х\.
Дадим индуктивное определение формулы над Б и реализуемой ею ФАЛ (это определение в отличие от [8] неявно предполагает наличие в Б ФАЛ, тождественно равной БП).
Любая БП xj из X считается формулой глубины 0 над Б, которая реализует ФАЛ, равную xj. Если для всех j, j = 1,... , к,, определена формула Tj глубины qj над базисом Б, которая реализует ФАЛ fj от БП из X, то запись вида
является формулой глубины q + 1 над Б, где
которая реализует ФАЛ / от БП из X такую, что / = уД:(/і,... , ДД. Так, запись вида
является формулой глубины 3 над базисом Д, которая реализует ФАЛ х\ Ф х2. Все записи, полученные в результате указанного индуктивного построения, и только они, считаются формулами над Б.
Важным частным случаем формул над базисом Д являются (см., например, [8]) дизъюнктивные нормальные формы (ДНФ). Напомним, что любую ФАЛ f(xі,...,ж„) можно представить ее совершенной ДНФ:
f(x 1,...,ж„)= V ад1(4.4)
о-=(о-1,...,о-„)е0
где, как обычно, xQ = х и х1 = х, a Nf множество тех наборов а, а Е Вп, для которых /(сг) = 1.
Индукцией по глубине каждой формуле глубины q над Б можно сопоставить упорядоченное корневое дерево глубины д, все ребра которого ориентированы к корню, каждому листу сопоставлена БП из X. а каждой внутренней вершине ФС из Б. Так, формуле xj соответствует "тривиальное" дерево с единственной вершиной, являющейся корнем и листом одновременно, которой сопоставлена БП Xj (см. рис. 4.2.а). Формуле Т вида (4.1) соответствует дерево D с корнем и, показанное на рис.
4.2.6, где Dj, j = 1,... , Д дерево с корнем ьу, которое соответствует формуле Tj. Граф, который получается из дерева D. соответствующего формуле Т. в результате "склеивания" листьев с одинаковыми пометками, называется квазидеревом, соответствующим формуле Т. На рис. 4.3.а показано дерево, а на рис. 4.3.6 квазидерево, которые соответствуют формуле (4.3).
Заметим, что формула по сопоставленному ей дереву или квазидереву восстанавливается однозначно.
Рассмотрим теперь более общую по сравнению с формулами модель модель схем из функциональных элементов (СФЭ), в которой последовательность операций суперпозиции базисных ФАЛ задается с помощью ориентированного ациклического графа, обобщающего квазидерево, и где возможно многократное использование промежуточных результатов.
Пусть X и Z счетные упорядоченные попарно не пересекающиеся алфавиты БП, причем БП из X (Z) считаются входными (соответственно, выходными) БП. Пусть по-прежнему Б, Б={9д}|=1,
полный базис, где ФАЛ рі, і = 1.....1. зависит от к,. к-, 1, БП и
является существенной ФАЛ, если /д 2.
По аналогии с упорядоченными деревьями ориентированнный граф G называется упорядоченным, если дуги, входящие в каждую его вершину и, упорядочены, т. е. пронумерованы числами 1,2,..., d+(v).
Определение. Схемой из функциональных элементов над базисом Б называется ориентированный ациклический упорядоченный граф Е, вершины которого помечены следующим образом:
1) каждый исток Е помечен некоторой БП из X, причем различные истоки помечены различными БП;
2) каждая отличная от истока вершина ? схемы Е помечена ФС рі, где /д = І{ {с):
3) некоторые вершины Е помечены выходными БП из Z так, что одной и той же вершине может быть сопоставлено несколько БП из Z, но разным вершинам не может быть сопоставлена одна и та же БП. При этом входные (выходные) БП, которые приписаны каким-либо вершинам Е, считаются входными (соответственно, выходными) БП Е, а те вершины, которым они сопоставлены, входами (соответственно, выходами) СФЭ Е.
Заметим, что квазидерево, соответствующее формуле над базисом Б, становится СФЭ над Б, если его корню приписать выходную БП. В связи с этим формулы над Б будем считать частным случаем СФЭ над Б. На рис 4.4.а показан пример СФЭ над базисом Eq с входными БП .Г|. Х2 и выходными БП zi, Z2, которая получена из квазидерева, приведенного на рис.
4.3.6, а на рис. 4.4.6 дано ее более "наглядное" изображение в виде сети (см. [6, с. 227-229]), построенной из соответствующих ФЭ.
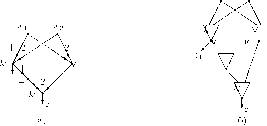
Рис. 4.4
Определим теперь функционирование СФЭ Е над базисом Б с входными БП х\, Х2, ¦ ¦ ¦, хп и выходными БП z\,, Zm. Сначала индукцией по д, д = 0,1,..., определим для каждой вершины ? глубины g в схеме Е реализуемую в ней формулу Т? = J-V(xі,... ,хп) глубины q над базисом Б. Если q = 0, т. е. ? вход Е, положим Т? = .г;. где xj входная БП, сопоставленная вершине ?. Пусть теперь ? вершина глубины д, ді, схемы Е, которая имеет пометку р{ и в которую входит кі дуг, причем дуга с номером j, lj?g, исходит из вершины vj глубины qj, где уже реализована формула Tj = Т?. глубины qj, а для чисел д, ді,..., д*. выполнено (4.2). Тогда в вершине ? реализуется формула Т = Т? вида (4.1), которая имеет глубину g + 1.
При этом считается, что в вершине ? СФЭ Е реализуется ФАЛ f(xі,...,ж„), если ФАЛ / реализуется формулой Тг. и что СФЭ Е реализует систему ФАЛ F, F = (/1,..., /т), или реализует систему булевых уравнений: Zl = /ь ..., гт = /т, если /і; j = 1,..., т, ФАЛ, реализованная в той выходной вершине СФЭ Е, которой приписана БП zj. Так, СФЭ на рис. 4.4 реализует систему ФАЛ (х\ ¦ ./л. х\ 0 х?) или систему уравнений: :| = .Г| - ./л. z% = х\ 0 х^. Схемы, реализующие одинаковые системы ФАЛ, называются эквивалентными.
Заметим, что изменение нумерации дуг, входящих в такую вершину ? СФЭ Е, которой сопоставлен ФЭ ?*- с симметрической ФАЛ ірі, не изменяет ФАЛ, реализуемую в вершине и, а значит, не влияет на функционирование Е. В связи с этим в подобных случаях номера дуг, входящих в вершину ?, могут не указываться.
Две СФЭ Е' и Е считаются изоморфными, если они изоморфны как помеченные графы, т. е. если существуют такие взаимнооднозначные отображения множества вершин Е' на множество вершин Е и множества дуг Е' на множество дуг Е, которые сохраняют отношение инцидентности вершин и дуг, а также все пометки. Из определения вытекает, что в соответствующих друг другу вершинах изоморфных СФЭ реализуются одинаковые формулы, а значит, и одинаковые ФАЛ.
Следовательно, две изоморфные СФЭ эквивалентны.
Пусть СФЭ Е' получается из СФЭ Е в результате удаления вершины ? и переноса начальной вершины всех дуг Е, исходящих из ?, а также всех выходных БП, приписанных ?, в отличную от нее вершину w, глубина которой в Е не больше, чем глубина ?. Тогда СФЭ Е' считается результатом применения к СФЭ Е операции удаления вершины ?, а вершина w называется преемником вершины ?. Тот факт, что СФЭ Е' получается из СФЭ Е в результате (многократной) операции удаления вершин из СФЭ Е, будем записывать в виде неравенства Е' Е. Схема Е называется тупиковой, если она не эквивалентна ни одной СФЭ Е' такой, что Е' Е.
Вершина СФЭ называется висячей, если из нее не выходит ни одна дуга и она не является выходом схемы. Две вершины СФЭ считаются эквивалентными, если в них реализуются равные ФАЛ. Применяя к СФЭ Е операцию удаления одной из двух эквивалентных вершин, преемником которой является другая вершина, мы получим СФЭ Е', которая, очевидно, эквивалентна Е.
Схема называется приведенной (строго приведенной), если в ней нет висячих (соответственно висячих и эквивалентных) вершин. Заметим, что тупиковая СФЭ является строго приведенной, и что из любой СФЭ можно получить эквивалентную ей приведенную (строго приведенную) СФЭ с помощью операции удаления висячих (соответственно висячих и эквивалентных) вершин.
Рассмотрим теперь задачу синтеза на примере СФЭ. Число ФЭ в СФЭ называется ее сложностью.
Сложность СФЭ Е обозначается через L(E). Для системы ФАЛ F через Lg(F) обозначим минимальную сложность тех СФЭ Е над базисом Б, которые реализуют F. Величина Lfi(F) называется сложностью системы ФАЛ F над базисом Б. При этом СФЭ Е, которая реализует F. и для которой L(E) = Ljy(F), считается минимальной СФЭ над базисом Б. Заметим, что СФЭ, показанная на рис. 4.4, является минимальной СФЭ над базисом Д, и что сложность системы ФАЛ F = (х\ - ./у. ад 0 ад) над базисом Д равна 4.
Введем, далее, функцию L^{n) натурального аргумента го, которая определяется следующим образом: