Алексеев В. - Элементы теории графов, схем, автоматов
Московский государственный университет имени М. В. Ломоносова
ВВЕДЕНИЕ
При изучении дискретных систем, в частности, систем преобразования информации, требуется строить математические модели, описывающие структуру или функционирование таких систем. В учебном пособии рассматриваются некоторые из таких моделей.
Одним из наиболее важных понятий, относящихся к структуре дискретных систем, является понятие графа. Это понятие, описывающее структуру связей между отдельными частями системы, в силу своей общности используется во многих математических моделях.
Графы очень часто используются в приложениях, поскольку они возникают как модель при изучении многих объектов. Например, структура молекулы является графом, в котором вершинами служат атомы, а ребрами валентные связи. Блок-схема алгоритма представляет собой орграф, в котором вершинами являются отдельные операторы, а дуги указывают переходы между ними.
Другие примеры графов: узлы и соединения в электрической цепи, схема дорог, множество предприятий с указанием двухсторонних связей между ними, группа людей с указанием их психологической совместимости, структура управления с указанием объектов и их подчиненности друг другу и т.д.
Тематика исследований, связанных с графами, очень широка. Это и исследование структуры и свойств графов, изучение специальных классов графов, построение быстрых алгоритмов для решения различных задач на графах и т. д. Здесь мы рассмотрим только некоторые простые вопросы, относящиеся к свойствам произвольных графов, а также рассмотрим два важных класса графов деревья и планарные графы, и изучим их свойства.
В настоящее время получили широкое распространение сложные преобразователи информации, которые составлены из простейших преобразователей (элементов) и в которых движутся сигналы нескольких типов, преобразуемые или передаваемые отдельными элементами в соответствии с определенными законами. В теории управляющих систем рассматриваются различные теоретико-графовые модели таких преобразователей, называемые схемами.
Каждая схема характеризуется структурой графом определенного вида и функционированием законом преобразования входных наборов или их последовательностей в выходные наборы или их последовательности. Функционирование схемы однозначно определяется ее структурой и функционированием элементов базиса набора простейших преобразователей, из которых построена схема.
При изучении схем решаются две основные задачи: задача анализа и задача синтеза. Задача анализа состоит в нахождении функционирования данной схемы, а задача синтеза в построении схемы, имеющей (реализующей) заданное функционирование. Каждая из этих задач может рассматриваться либо как индивидуальная задача, и тогда ее решением является конкретное функционирование (схема), либо как массовая задача, и тогда ее решением должен быть алгоритм нахождения функционирования (схемы). Задача синтеза имеет, как правило, множество решений, из которых выбирают решение, оптимальное по какому-либо критерию.
Чаще всего в качестве такого критерия выступает сложность схемы, понимаемая как сумма сложностей составляющих ее элементов.
В §§4-7 мы мы рассмотрим, как решается задача синтеза для схем из функциональных элементов для преобразователей без памяти, реализующих некоторые системы булевых функций. В §§8-9 рассматриваются автоматы-преобразователи с памятью, работающие по тактам в дискретном времени.
Кроме задач анализа и синтеза автоматов, которые рассматриваются в §8, изучаются также эксперименты с автоматами (§9), что тесно связано с тестированием вычислительных устройств.
Часть 1. Графы
§ 1. Основные понятия теории графов
Определение. Графом G (в широком понимании) называется любая пара (\Е). где V = {щ, ?’25 - - - } множество элементов любой природы, а Е = {еі,в2,...} семейство пар элементов из V, причем допускаются пары вида (и,, и,) и одинаковые пары.
Если пары в V рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным (орграфом).
Элементы множества V называются вершинами графа, а пары из Е его ребрами; в орграфе они называются ориентированными ребрами или дугами.
Говорят, что ребро е = (и, ?) в неориентированном графе соединяет вершины и и и, а в ориентированном графе дуга е = (и, ?) идет из вершины и в вершину ?.
Графы можно условно изображать следующим образом. Вершины будем изображать точками, а каждое ребро (дугу) (щ, vj) Е Е линией, еоодипяюшей точки, соответствующие щ и vj.
Если (vi,vj) дуга, то на этой линии будем указывать стрелку от и,; к vj.
На рис. 1.1 приведены неориентированный и ориентированный графы G = (?,Е), где V = {1,2,3,4}, Е = {еь е2, е3, е4, е5, еб, е7} и б1 = (1,2), е2 = (2,3), е3 = (3,4), е4 = (4,2), е5 = (1,4), еб = (4,2),
е7 = (1, !)-
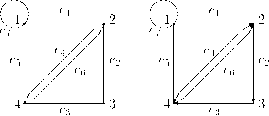
Рис. 1.1.
Пара вида (д,;, и,;) называется петлей в вершине щ. Если пара (vi, Vj) встречается в Е более одного раза, то говорят, что (v^vj) кратное ребро. В графах на рис.
1.1 (4, 2) кратное ребро, ej петля.
Замечание. Часто в литературе под графом понимается граф без петель и кратных ребер.
В этом случае граф с кратными ребрами называют мультиграфом, граф с кратными ребрами и петлями псевдографом.
Графы очень часто используются в приложениях, поскольку они возникают как модель при изучении многих объектов. Например, структура молекулы является графом, в котором вершинами являются атомы, а ребрами валентные связи.
Блок-схема алгоритма представляет собой орграф, в котором вершинами являются отдельные операторы, а дуги указывают переходы между ними. Другие примеры графов: элементы и соединения в электрической цепи, схема перекрестков и дорог, множество предприятий с указанием двухсторонних связей между ними, группа людей с указанием их психологической совместимости, структура управления с указанием объектов и их подчиненности друг другу и т. д.
Определение. Говорят, что вершины ту и Vj смежны в графе G = (\'. Е). если в Е входит пара (ту, ту) или (иу,гу).
Говорят, что ребро (дуга) (ту;,vj) инцидентно вершинам ту и vj.
Определение. Степенью вершины в неориентированном графе называется число ребер, инцидентных данной вершине, при этом петли учитываются дважды.
Вершины степени 0 называют изолированными.
Например, в неориентированном графе на рис. 1.1 степень вершины 3 равна 2, степени остальных вершин равны 4.
Теорема 1.1. Пусть в графе G р вершин и q ребер.
Пусть deg гу степень вершины гу. Тогда
р
deg ?і = 2q.
І= 1
Доказательство. Когда мы считаем степень одной вершины, мы считаем все ребра, выходящие из нее.
Вычисляя сумму всех степеней, мы получаем, что каждое ребро считается дважды, так как оно инцидентно двум вершинам (петли по определению степени также посчитаются дважды). Поэтому общая сумма будет равна удвоенному числу ребер.
В ориентированном графе можно определить степень так же, как в неориентированном графе, если не учитывать ориентацию. Кроме этого, для ориентированных графов вводится следующее определение.
Определение. Полустепенью исхода dr {у) (полустепенью захода d+(v)) вершины ? в ориентированном графе называется число дуг, выходящих из данной вершины (соответственно входящих в данную вершину).
Легко видеть, что в любом ориентированном графе выполняется равенство
Е deg (л) = Е deg+(u,:),
і= 1 і= 1
поскольку в обеих частях равенства каждая дуга учитывается ровно 1 раз.
Для человека удобно геометрическое представление графа, такое, например, как на рис 1.1. В компьютере используют другие, "более дискретные", способы представления графов.
Один из наиболее распространенных способов представление графа матрицей смежности.
Определение. Пусть граф G имеет р вершин и пусть его вершины занумерованы числами 1,2,...,р. Матрица с р строками и р столбцами называется матрицей смежности графа G, если для любых lip и 1 jp a[i,j] равно числу ребер (дуг), идущих из вершины і в вершину j.
Например, графы, изображенные на рис. 1.1, представляются следующими матрицами смежности.
/1 1 0 1 ^ (1 1 0 1 \ 1 0 1 2 0 0 1 0 0 1 0 1 0 0 0 1 I1 2 1 ч 1 2 0 0/
При представлении графа матрицей смежности легко выполняются операции добавления или выбрасывания ребра (соответствующий элемент матрицы просто увеличивается или уменьшается на 1), легко считается степень вершины і (достаточно просуммировать числа в г-ой строке, диагональный элемент взяв дважды). В целом, матрицы смежности очень удобны.
Однако, если в графе мало ребер, то представление графа матрицей смежности может быть не очень хорошим. Например, если в графе 50 вершин, то матрица будет иметь 2500 элементов, хотя в графе может оказаться лишь несколько сотен ребер. В таких случаях используют списки смежностей. Для каждой вершины образуется список, в который заносят все вершины, в которые из данной вершины идут ребра (дуги).
Например, графы, изображенные на рис. 1.1, представляются следующими списками смежностей
1: 1, 2, 4;
1: 1, 2, 4; 2: 3;
3: 4;
4-9 9
2: 1, 3, 4, 4; 3 : 2, 4;
4-1 9 9 3
При представлении графов списками смежностей и при динамическом изменении графов необходимо использовать алгоритмы работы со списками, что хорошо реализуется в ряде алгоритмических языков.
При изучении структуры графов некоторые графы можно не различать.
Определение. Пусть G\ = (Г|. Е\) и G- = (IT Е- ) два графа.
Тогда G\ и (j?2 называются изоморфными, если существуют взаимно однозначные отображения р\ : ?\ ТД р2 '¦ Е\ Е2 такие, что для любого ребра (дуги) (и,?) G Е выполняется (f2(u,v) = (pi(и), 991(c)). Другими словами, соответствующие ребра должны соединять соответствующие вершины.
Для графов без петель и кратных ребер это определение эквивалентно следующему более простому определению.
Определение (для графов без петель и кратных ребер). Графы G\ = (Hi, Еі) и Г?2 = (V2, Е2) называются изоморфными, если существует взаимно однозначное отображение р : ?\ ?2 такое, что
(и, ?) G Еі (р(и),р(?)) G Е2.
Рассмотрим теперь некоторые понятия, связанные с внутренней структурой графа.
Определение. Граф G\ = (Уі,?і) называется подграфом графа G = (У, Е), если Уі С V и Ех С Е.
Определение. Путем в графе (орграфе) G = (У, Е) называется последовательность вершин и ребер (дуг) вида
где все и,; G Е и все (г,;,-и,;+1) G Е. Длина пути это число ребер (дуг) в нем. Говорят, что этот путь идет из vq в ?п.
Цепь это путь без повторяющихся ребер (дуг), простая цепь путь без повторяющихся вершин.
Лемма 1.1. Из любого пути, идущего из vq в ?п, где vq ф ?п, можно выделить подпуть из vq в ?п, являющийся простой цепью.
Доказательство. Пусть данный путь не простая цепь.
Тогда в нем повторяется некоторая вершина и, то есть он имеет вид: Р\ = ?§Сі?С2?С%?п. Тогда он содержит подпуть Н = vqC\vC$vn.
Если в Н повторяется некоторая вершина, то аналогично удалим еще кусок и т. д. Процесс должен закончиться, т. к. Р\ конечный путь.
Определение. Путь называется замкнутым, если ?п = vq.
Путь называется циклом, если ?п = vq и ребра (дуги) не повторяются. Путь называется простым циклом, если ?п = vq и больше нет повторений вершин.
Далее под графом будут пониматься только конечные неориентированные графы.
Определение. Граф G = (\'.
Е) называется связным, если для любых двух вершин г/, г; Е V в G существует путь из г/ в г/.
Отношение "существует путь из вершины ? в вершину w в графе СГ является отношением эквивалентности на множестве вершин. Поэтому, если граф G не связный, то его вершины можно разбить на несколько подмножеств так, что вершины в одном и том же множестве можно соединить путем, а вершины из разных множеств нельзя соединить путем.
Каждое такое множество вершин вместе с ребрами графа G, соединяющими эти вершины, называется связной компонентой графа G. Так, например, граф на рис. 1.2 имеет 3 связных компоненты.

Рис. 1.2.
Докажем теперь несколько вспомогательных утверждений о связности и циклах, которые потребуются нам в дальнейшем.
Лемма 1.2. Если граф G = (V, Е) связный и а ? V, Ъ Е V, а ф Ъ, и (аД) ^ Е, то при добавлении к графу G ребра (а,Ь) в полученном графе будет простой цикл.
Доказательство. Так как G связный граф, то в нем есть путь из а в Ъ. Тогда по лемме 1.1 в G есть простая цепь С из а в Ь. Поэтому в полученном графе есть цикл С, (6, а), а.
Лемма 1.3. Если граф G = (?,Е) связный и ребро (аД) содержится в некотором цикле в графе G, то при выбрасывании из графа G ребра (аД) снова получится связный граф.
Доказательство. Это утверждение следует из того, что при выбрасывании из графа G ребра (а, Ь) вершины а и Ъ все равно остаются в одной связной компоненте, поскольку из а в Ъ можно пройти по оставшейся части цикла.
Лемма 1.4. Пусть в графе G = (V, Е) р вершин и q ребер.
Тогда в G не менее p q связных компонент. Если при этом в G нет циклов, то G состоит ровно из р q связных компонент.
Доказательство. Пусть к некоторому графу Н, содержащему вершины и. ?, добавляется ребро (и. с).
Тогда если и. ? лежат в разных связных компонентах графа Н, то число связных компонент уменьшится на 1. Если и, ? лежат в одной связной компоненте графа Н, то число связных компонент не изменится. В любом случае число связных компонент уменьшается не более чем на 1. Значит при добавлении q ребер число связных компонент уменьшается не более чем на q. Так как граф G получается из графа G\ = (V,) добавлением q ребер, то в С? не менее p q связных компонент. Пусть теперь в G нет циклов, и пусть в процессе получения G из G\ добавляется ребро (и,?). Если бы м, ? лежали уже в одной связной компоненте, то в G, согласно лемме 1.2, возникал бы цикл.
Следовательно, и, ? лежат в разных связных компонентах и при добавлении ребра (м, ?) число связных компонент уменьшается ровно на 1. Тогда G состоит ровно из p q связных компонент.
Следствие. Если qp 2, то любой граф с р вершинами и q ребрами не связен.
Доказательство. По лемме 1.4 число связных компонент не менее р q2.
Если граф G с р вершинами задан матрицей смежности А, то быстрое нахождение связных компонент можно осуществить следующим образом. Рассмотрим матрицу Д порядка р. в которой на диагонали стоят 1, = 1, если a(i. j) 0 и Д(іД) = 0, если a(i. j) = 0.
Тогда равенство Д(іД) = 1 равносильно тому, что из вершины с номером і в вершину с номером j существует путь длины не более 1. Определим теперь матрицу Д порядка р. в которой Д(і.Д) = 1 тогда и только тогда, когда из вершины с номером і в вершину с номером j существует путь длины не более к. Легко понять, что все матрицы Д при кр 1 совпадают и элемент с номером (г, j) в них равен 1 тогда и только тогда, когда из вершины с номером і в вершину с номером j существует хотя бы один путь. Обозначим такую матрицу /оо. Рассмотрим операцию умножения матриц, которая отличается от обычного умножения только тем, что вместо сложения используется дизъюнкция.
Тогда легко видеть, что Д+і = Д ¦ І\.
Утверждение. Пусть р 12т. Тогда матрицу можно получить из матрицы Д, используя не более 2р?іт операций конъюнкции
и дизъюнкции.
Доказательство. Будем последовательно вычислять матрицы /2, /4, U. .... /2™, возводя предыдущую матрицу в квадрат.
Возведение матрицы в квадрат (по обычному правилу: "строчка на столбец") требует не более 2р?і операций конъюнкции и дизъюнкции. Доказываемое утверждение следует из того, что П- = / х . поскольку р 12'.
§ 2. Деревья
Определение. Граф G = (?,Е) называется деревом, если он связный и не содержит циклов.
Вершины степени 1 в дереве называют его листьями.
Определение. Подграф G\ = (?і,Еі) графа G = (?,Е) называется оетовным деревом, если G\ дерево и ?\ = V.
Теорема 2.1. Любой (конечный) связный граф G = (V, Е) содержит хотя бы одно остовное дерево G\ = (?,Еі).
Доказательство. Если в G нет циклов, то положим G\ = G. Если в G есть циклы, то удалим из G какое-нибудь ребро, входящее в цикл. Получится некоторых! подграф G' . По лемме 1.3 G' связный граф. Если в G' нет циклов, то положим G\ = G', иначе продолжим этот процесс.
Процесс должен завершиться, так как Е конечное множество.
Теорема 2.2. Пусть в дереве G имеется р вершин и q ребер. Тогда q = р 1.
Доказательство. Так как G связный граф и G не содержит циклов, то р q = 1 по лемме 1.4. Отсюда q = р 1.
Понятие дерева можно определить различными способами, что вытекает из следующей теоремы.
Теорема 2.3. Пусть G = (V, Е) неориентированный граф без петель и кратных ребер, \?\= р, \Е\ = q. Тогда следующие 5 условий эквивалентны:
1) G дерево:
2) G без циклов и q = р 1;
3) G связный и q = р 1;
4) G связный, но при удалении любого ребра становится несвязным:
5) G без циклов, но при добавлении любого нового ребра на тех же вершинах появляется цикл.
Доказательство. Докажем с л едущие переходы 1) == 2) == 3) == 4) = 5) = 1). откуда будет следовать, что из любого условия вытекает любое другое.
Переход 1) =4- 2) следует из теоремы 2.2. Пусть теперь выполняется 2). Тогда по лемме 1.4 в С? число связных компонент равно р q = 1, то есть G связный граф.
Отсюда следует переход 2) 3). Переход 3) =- 4) вытекает из следствия к лемме 1.4. Пусть
выполняется 4). Тогда если бы в G был цикл, то при удалении любого ребра из этого цикла G остался бы связным, согласно лемме 1.3. Это противоречило бы 4). Значит G не имеет циклов.
Вторая часть условия 5) вытекает, согласно лемме 1.2, из того, что G связный. Таким образом, получаем, что 4) =- 5).
Пусть выполняется 5). Если при этом G не связный граф и вершины м, ? лежат в разных связных компонентах графа G, то добавление к G ребра (и, с), очевидно, не порождает циклов, что противоречит 5).
Отсюда следует, что G связный граф, то есть 5) =- 1). Теорема доказана.
Условия 4) и 5) показывают, что множество всех деревьев это множество всех минимальных связных графов и, в то же время, множество всех максимальных графов без циклов.
Для представления данных в информационных системах, в справочниках, при реализации алгоритмов поиска и в других приложениях часто используются корневые деревья, то есть деревья с выделенной вершиной, именуемой корнем. Мы дадим следующее индуктивное определение корневого дерева.
Определение. 1) Граф, имеющий одну вершину и, которая выделена, и не имеющий ребер, является корневым деревом с корнем
?.
2) Пусть Д, Д,..., Dm, где ml корневые деревья с корнями ?’і, и2, - - - , ?т. Пусть Д = (К:, Д) и Ц П V} = при і Д j. Пусть ? ? ?\ U 12 U... U ?т. Тогда граф D = (У, Е), где V = ?\ U Д U...
U ?т U {и}, Е = Е\ U Е'2 U... U Ет U {(?, ? 1),..., (и, ?т)} и выделена вершина ?, является корневым деревом с корнем ? (см. рис.
2.1). При этом Д,Д,..., Dm называются поддеревьями корневого дерева D.
D\ Д Dm
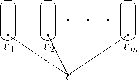
Рис. 2.1.
3) Только такие графы называются корневыми деревьями, которые могут быть построены по 1) и 2).
Например, файловая структура в компьютере является корневым деревом. При этом корню соответствует сам компьютер, вершинам второго яруса соответствуют диски А, В, С, D и т. д., вершинам третьего яруса соответствуют директории, вершинам следующих ярусов соответствуют поддиректории и файлы.
Определение. Упорядоченное корневое дерево это корневое дерево D, в котором задан порядок его поддеревьев D\.
D2, . . ., Dm (можно считать, что числами 1,2,..., m занумерованы ребра, выходящие из корня дерева D) и каждое Dj само есть упорядоченное корневое дерево.
Теорема 2.4. Число упорядоченных корневых деревьев с q ребрами не превосходит 49.
Доказательство. Рассмотрим важный для приложений способ обхода упорядоченного корневого дерева, который называют "поиском в глубину". Этот обход описывается рекурсивно следующим образом. 1) Начать из корня дерева D: 2) пока есть поддеревья, перейти по ребру в корень очередного поддерева, рекурсивно обойти это поддерево "в глубину", вернуться в корень исходного дерева.
В результате обход "в глубину" проходит по каждому ребру дерева D ровно 2 раза: один раз при переходе в очередное поддерево, второй раз при возвращении из этого поддерева. В соответствии с обходом "в глубину" будем строить последовательность из 0 и 1, записывая на каждом шаге О или 1, причем 0 будем записывать, если происходит переход в очередное поддерево, а 1, если мы возвращаемся из поддерева.
Получим последовательность из 0 и 1 длины 2д, которую назовем кодом дерева D. По этому коду однозначно восстанавливается дерево D. поскольку каждый очередной разряд однозначно указывает, начинать ли строить новое очередное поддерево или возвращаться на ярус ближе к корню. Таким образом, упорядоченных корневых деревьев с q ребрами не больше, чем последовательностей из 0 и 1 длины 2д, а их число равно 229 4
Изоморфизм корневых деревьев определяется так же, как изоморфизм обычных графов, но дополнительно требуется, чтобы корню одного дерева сопоставлялся при изоморфизме корень другого дерева. Для упорядоченных корневых деревьев дополнительно требуется, чтобы при изоморфизме сохранялась упорядоченность.
Следствие. Число неизоморфных корневых деревьев с q ребрами и число неизоморфных обычных деревьев с q ребрами не превосходит 4q.
Доказательство. Выделяя в неизоморфных деревьях по одной точке, мы получим неизоморфные корневые деревья.
Упорядочивая поддеревья в неизоморфных корневых деревьях, мы получим различные упорядоченные корневые деревья. Поэтому число неизоморфных деревьев е q ребрами не превосходит числа неизоморфных корневых деревьев е q ребрами, которое, в свою очередь, не превосходит числа различных упорядоченных корневых деревьев е q ребрами.
Отсюда и из теоремы 2.4 получаем доказываемое следствие.
Отметим, что корневые деревья часто рассматривают как ориентированные.
Определение. Ориентированным деревом называется корневое дерево, все ребра которого ориентированы к корню.
В ориентированных деревьях нет ориентированных циклов. Но это не единственные графы, обладающие этим свойством.
Определение. Ориентированным ациклическим графом называется любой ориентированных! граф, в котором нет ориентированных циклов.
Определение. Вершина ориентированного графа называется истоком (стоком), если в нее не входит ни одна дуга, то есть d+(v) = О, (соответственно, из нее не выходит ни одной дуги, то есть d~(v) = 0.
Утверждение 1.1. В любом (конечном) ориентированном ациклическом графе есть хотя бы один исток и хотя бы один сток.
Доказательство. Выберем любую вершину и будем строить путь из нее, двигаясь произвольно по направлению дуг. При этом вершины не могут повторяться, так как в данном орграфе нет ориентированных циклов. Поэтому путь должен прийти в тупик, которых! и является стоком.
Для получения истока надо аналогично строить путь, двигаясь против направления дуг.
Определение. Глубиной вершины ? в ориентированном ациклическом графе называется максимальная длина ориентированного пути из всех истоков в вершину ?.
Это определение корректно в силу утверждения 1.1. При этом глубина каждой вершины в ориентированном ациклическом графе не превосходит р 1, где р число вершин в графе.
Утверждение 1.2. Пусть (и,?) дуга в ориентированном ациклическом графе. Тогда глубина вершины ? больше, чем глубина
вершины и.
Доказательство следует из того, что если из некоторого истока в вершину и существует ориентированных! путь длины к, то из того же истока в вершину ? существует ориентированных! путь длины к + 1.
§ 3. Планарные графы
Пусть задан неориентированных! граф G = (V, Е). Пусть каждой вершине и,; из V сопоставлена точка а* в некотором евклидовом пространстве, причем а,; ф aj при і ф j. Пусть каждому ребру е = (гу, vj) из Е сопоставлена непрерывная кривая L, соединяющая точки а* и aj и не проходящая через другие точки а*.