Алгоритм решения задачи нижнего уровня
Определим минимальный отрезок [х1, х2], которому принадлежит точка Х0 , где х1, х2 - точки разрыва функции ft (х) .
Точки разрыва функции fi2 ( х) определяются матрицей X = {х.} е Rmxmax(N(lследовательно х1, х2 совпадают с соответствующими элементами строки i2 матрицы X.
Пусть х1 = хг2. ,х2 = х2/+i, где Х2. , Х2/+і - элементы магри-цы X. Тогда исходная задача разбивается на две подзадачи с измененными начальными условиями - происходит ветвление:
Левая ветвь: N(i2) = j1 (уменьшаем количество рассматриваемых вариантов по проекту i2). Значения элементов матриц
X = {Xj } и F = {fj} остаются прежними для i = 1, m, j = 1,..., N (i) (с учетом изменения количества вариантов по проекту i2)-
ПРавая ветвь: хі2j = ^j+h+i, j = 1,...,N(i) - j1 -1,
Aj = f4i+h +1’ j = 1,.N(i) - ji - 1’ (сдвигаем гРафики функций
А(х) и А(х))’ K = K - \j+л +1’ х0 = xi2j+j +1 (вклаДываем в проект i2 величину средств хІ2.+j +1 : считаем выбор данного проекта приоритетным в начальный момент).
Для каждой ветви производится расчет матриц S = {sij.},
X' = {х?. } е Rmxmax(N'(l)) и F' = {f } e Rmxmax(N'(l)), определяющих соответствующие функции f (х), и вычисляются вектора X0={х0} и F0 = {f0} (при этом для правой ветви элемент i2 вектора X0 = {х0} - ненулевой).
Расчеты данных величин производятся аналогично вышеописанному алгоритму.
В случае если для распределения подзадачи не выполняется условие х0 = х\с , Vi = 1,...,m , то происходит дальнейшее ветвление подзадачи.
Результатом ветвления является дерево, в листьях которого будут определены текущие решения (X0, F0, S, J *) каждой подзадачи, для которых проверяется существование решения задачи нижнего уровня.
Построение дерева и выбор оптимального решения, на котором достигается максимум целевой функции, осуществляется рекурсивно.
Алгоритм решения задачи нижнего уровня.
Текущим решением задачи верхнего уровня является набор проектов (с соответствующим выбором подрядчиков), реализация которых возможна при ограничении на общий объем инвестиций K = PVG+.
Для выбранного набора проектов необходимо определить возможность их реализации при ограничениях на состояние счета заказчика.
Условие неотрицательности баланса счета заказчика формулируется следующим образом:
t m t
t = о,...,т XgkV +XX(j -с‘,-У о,
к=о i=1 к=0 ]і ]і
t
где Xgkv - приведенная величина кредитного потока на момент
к=0
времени t, XX (г-~ с ¦* )vk - суммарный баланс по всем проек-г=1 к=о j Уі там на момент времени t.
Текущее решение задачи верхнего уровня определяет следующие параметры: X0 = {хг}, i = 1, m - вектор, элементы которого определяют распределение инвестиций в проект г; F0 = {f0}, i = 1, m - вектор, элементы которого определяют
отдачу от инвестиций по проекту i; S = X f - суммарная отдача
г=1
от инвестиций - целевая функция задачи, J* = {j*,..., j*m} - номера вариантов, реализуемых по проекту i (в случае, если по проекту i выбран вариант с номером, j j* е J*, а для остальных проектов
номера вариантов принадлежат J* , то реализация такого набора проектов невозможна при заданных ограничениях на объем инвестиций).
Если для решения (X0, F0, S, J *) выполняется условие неотрицательности баланса счета заказчика, то данное решение является решением задачи нижнего уровня и происходит возврат на верхний уровень.
Заметим, что решение, характеристики которого заданы вектором J' = j ,..., j'm }, где j\ ? j* при i = 1,..., n, также удовлетворяет ограничениям на общий объем инвестиций, так как элементы соответствующего вектора X' = {х'г }, i = 1,...,m не
превосходят элементы вектора X0 = {х0}, i = 1, m, а элементы
вектора F' = {f V } не превосходят элементы вектора F0 = {fi0}.
Таким образом, текущее решение задачи верхнего уровня (X0, F0, S, J*) определяет множество D допустимых решений при ограничении на общий объем инвестиций, причем решение (X0, F0, S, J*) является на множестве D наилучшим, так как сумма S является на данном множестве максимальной.
В случае, если текущее решение задачи нижнего уровня (X0, F0, S, J ) не удовлетворяет ограничениям на состояние счета заказчика, необходимо решить задачу нижнего уровня, т.е. определить наилучшее решение (X', F', S, J') е D, на котором выполняется условие неотрицательности счета заказчика - решение, для которого значение S будет максимальным на множестве допустимых решений D.
Решение (X', F', S, J') е D будет являться решением соответствующей подзадачи верхнего уровня. Выбор оптимального решения задачи, на котором достигается максимум целевой функции, будет осуществляться с учетом соответствующего значения величины S .
Задача нижнего уровня решается следующим образом. Вектор J * = {/і?, jm} определяет фиксированный набор вариантов, из которых осуществляется выборка решения (X', F', S, J') е D задачи нижнего уровня.
В соответствии с начальными условиями заданы матрицы
X = {ху.} е Rmxmax(N(i)) и F = {f } е Rmxmax(N(i)). Элементам строки
i данных матриц соответствуют точки разрыва кусочнопостоянной функции f(x).
Так как функции f(х) являются неубывающими, то элементы строк матрицы F = {f. } е Rmxmax(N(i)) упорядочены по возрастанию.
Обозначим N (i), i = і,...,m - количество вариантов реализации, которые не были отброшены для проекта i на верхнем уровне:
N (i) = j . Тогда решение задачи верхнего уровня (X , F , S, J ) определяет выборку элементов матрицы X = {xij }e R
mxmax( N (i))
m xmax( N (i))
величина инвестиций в проект i в случае выбора варианта реализации с номером j; f. - значение приведенной стоимости проекта i (отдача от инвестиций) в случае выбора варианта j.
Обозначим J1 = {j1}, где j1 = j* -1 (i = 1,...,m): вектор,
компоненты которого определяют величину инвестиций и отдачу от инвестиций в проект i в случае выбора варианта с номером
]г - 1 ¦
Введем вспомогательный вектор J2 = {j2), i = 1,..., m . Начальные условия: J2 = {j2} = 0. Обозначим S1 = {у1}, i = 1,...,m -
вектор, компоненты которого определяют суммарную отдачу от инвестиций в случае, если для проекта i выбирается вариант с номером ji1 , а по остальным проектам выбираются варианты с
номерами j*: S = {s1}, j ^ m, где s1 = X fkN'(k) + fN-(l).
1 k m,k * l
1i m
Пусть Smax - максимальная суммарная отдача от инвестиций, Smax = max s/, при этом i1 = (ils1 = Smax) - номер проекта, при
котором достигается максимальное значение si1 . Определим: X' = {xlb где х]= x при j m,j *|i, x. = x.iN.(.i)-15
F' = {fi}, где fi = fi при 1 = 1,¦¦¦, m, i * ^ f = 4n'(i1)-1’
S=X f, S = Smx, J' = O' }, где j\ = N' (li) -1.
Тогда решение (X', F', S', J') является наилучшим на множестве D за исключением решения (X0, F0, S, J ).
Проверим выполнение условия неотрицательности баланса счета заказчика для решения (X', F', S', J'): t = 0,..., n
Zg-y + ZZ(rj
c‘.)vk 0.
Vi '
Если условие выполнено, то решение (X',F', S', У ) является решением задачи нижнего уровня. Если условие не выполняется, то задача нижнего уровня разбивается на две подзадачи с измененными начальными условиями - происходит ветвление задачи:
Левая ветвь: Считаем текущим решением задачи верхнего уровня решение (X', F', S', J'). При этом для решения (X', F', S', J') условие неотрицательности баланса счета заказчика не выполняется (условие проверено на предыдущем этапе).
Тогда элементы матрицы F = {f} е Rmxmax(N(i)); f_, = о
при k=1,...,N'(i1)- j . Элементы матрицы X = {xi;j}еRmxmax(N(i)); x. = 0 при к = 1, ..., N' (іі) - j,, N' (ii) = j', , при i * ii вели-
llJ i2 +k 1 1
чины N (i) остаются прежними.
Определяем вектора J1 = {j1}, S1 = {s1}: (i = 1,...,m) при
данных начальных условиях: J1 = {j1} , при этом j1 = j при j; Ф0, S1 = {S}: при i: j] = 0, s,1 = Z f„,;k,( + f„.
’ iN (i)
1k m,k фі;і: j =0
при i: ji Ф 0, Si = 0.
Определяем величины Smax = max si1, i1 = (ils1 = Smax). Если
1im
J1 = {j1} = 0 для i = 1,..., m и Smax = S' или i = 1,..., m
S1 = {s1} = 0, то решение данной подзадачи не существует.
Иначе в соответствии с вышеописанным алгоритмом вычисляем решение (X,F,S,J) (наилучшее решение на множестве D, которое определяется решением (X',F',S', J')).
Проверяем выполнение условия неотрицательности баланса счета заказчика для решения ( X'', F' ', S' ', J' ') . Если условие выполнено, то решение (X,F,S,J) является текущим решением задачи нижнего уровня.
Если условие не выполнено, то необходимо осуществить дальнейшее ветвление задачи.
Правая ветвь: считаем, что для проекта с номером i1 рассматривается только вариант с номером j* . Изменяем вектор
их max( N (i))
J2 = {j2): j = j. Изменяем матрицы X = {хі}.}eR
m xmax( N (i))
F = {fj} e R ' ' , определяющие величину инвестиций и отдачу от инвестиций в проект i в случае выбора варианта реализации с номером j:. fhl = f fij = 0, j = 2, ..., j* - 1
xi 1 = x. ,, xi = 0 , j = 2, - 1.
ii1 iiJi ’ hJ J11
Изменяем значения N (i): N'(i1) = 1, при i Ф i1 величины N (i) остаются прежними. При данных начальных условиях определяем вектора: J1 = {j1} , при этом j1 = ji при ji Ф 0, S = {si}: при i: /2 = 0, s1 = V f , + f , при i: /2 Ф 0
1k m,k фі;і: ji =0
г Ji ’ i J kN (к) iN (i) г Ji
sii = 0.
Если i = 1,..., m S1 = {s1} = 0 i = 1,...,m , то решение данной подзадачи не существует. Иначе вычисляем значения величин
Smax = и i1 = (i'|s1 = Smax)-
Определяем решение (X, F, S, J) и проверяем для него условие неотрицательности баланса счета заказчика. Если условие выполнено, то решение (X,F,S,J) является текущим решением задачи нижнего уровня.
Если условие не выполнено, то необходимо осуществляется дальнейшее ветвление задачи.
Результатом ветвления задачи нижнего уровня является множество Di решений вида (X', F', S', J') , для которых выполняется условие неотрицательности баланса счета заказчика.
Решением задачи верхнего уровня является решение (X', F', S', J') e D1, для которого соответствующее значение S’
является максимальным. 132
Примеры расчетов по приведенным в настоящем разделе алгоритмам можно найти в [24].
Таким образом, в настоящем разделе сформулирована и решена оптимизационная задача планирования, заключающаяся в выборе вариантов реализации корпоративных проектов.
Имея результаты решения общей задачи согласования интересов (и выбора управляющей компании) в системе управления корпоративными программами (раздел 1) и задачи планирования (настоящий раздел), перейдем к постановке и решению задач оперативного управления процессом реализации корпоративных проектов и программ.
Механизмы оперативного управления процессом реализации корпоративных проектов и программ
В настоящем разделе анализируется динамика реализации корпоративных проектов и программ. В том числе, с точки зрения управляющей компании и активных элементов анализируются взаимные платежи и риски, вызванные возможностью невыполнения сторонами взятых на себя обязательств, а также ошибками прогнозирования и планирования.
Шкалы оплаты. При расчетах центра (УК) с АЭ - исполнителями работ по проекту, входящему в корпоративную программу, размер оплаты, получаемой АЭ, зависит от процента выполнения работ.
В качестве процента выполнения, в частности, могут выступать показатели освоенного объема [29].
Предположим, что сумма договора или стоимость работы или пакета работ по проекту согласована центром и АЭ и равна C. Шкалой оплаты называется кумулятивная зависимость размера вознаграждения (доли от стоимости договора), выплаченного центром АЭ, от процента выполнения [18, 43].
Обозначим через f процент выполнения, через g - процент от суммы C, выплаченный АЭ. Тогда шкалой будет зависимость g(f). Эта зависимость обладает следующими свойствами [18]:
- функция g( - ) - неубывающая и непрерывная справа;
- g(0) = 0;
- ^ b е [0;1] gb е [0; 1];
- 7(1) = 1.
Если ввести зависимость о[р) размера вознаграждения, получаемого АЭ (а не уже полученного за весь выполненный к рассматриваемому моменту времени объем работ) от процента выполнения, то, очевидно, что этот размер вознаграждения с точностью до мультипликативной константы (стоимости договора) совпадает со скоростью изменения уже полученных АЭ сумм, то есть, если g(0 - кусочно-дифференцируемая функция, то
dy(b)
db
b е [0; 1].
(1) s(b) = C
Верно и обратное соотношение:
1 b
(2) 7(b) = - j s(w)dw .
C 0
Из выражений (1) и (2) следует, что на участках возрастания о(0 функция ХО является выпуклой, на участках убывания о(0 функция Х0 является вогнутой, а в точке максимума о(0 функция Х0 имеет перегиб. Кроме того, выполняется условие нормировки:
і
(3) j s (w)dw = C.
0
В [18, 43] перечисляются типовые решения, то есть типовые шкалы оплаты: равномерная оплата, при которой вознаграждение АЭ за каждую единицу процента выполнения одинаково; аккордная оплата, при которой вся сумма договора C выплачивается только в момент полного выполнения работ; -процентная предоплата (а е [0; 1]), при которой сумма a C выплачивается в момент начала работ, а сумма (1 - a) C - в момент полного завершения работ, и др. - любой определенной на отрезке [0; 1] измеримой функции соответствует некоторая шкала.
Рассмотрим динамику реализации одного проекта. Для простоты допустим, что действием АЭ является выбор интенсивности y 0, которая предполагается постоянной в ходе реализации проекта и характеризует затраты исполнителя в единицу времени.
Если V 0 - объем работ по проекту, то, очевидно, что время T = Т(у) завершения работ равно
(4) T(y) = V /у.
Если интенсивность постоянна, то объем v(t, а) работ, измеряемый затратами исполнителя, изменяется линейно:
v(t, у) = у t, t е [0; T].
Предположим, что предъявляемый АЭ результат реализации проекта является функцией W(-) от относительного объема выполненных работ v(t, у) / V, то есть, центром наблюдается процент выполнения
(5) b(t, У) = W(y t / V).
Относительно функции W(-) предположим, что она имеет S-образный вид, то есть удовлетворяет следующим требованиям:
- W(0) = 0, W(1) = 1, W’(0) = 0;
- W(-) - строго монотонно возрастающая гладкая функция;
- $р’ е (0; 1): р е [0; р’] W’’(p) 0,
р е [р’; 1] W’’(p) ? 0.
Имея шкалу у(р) и зная зависимость (5) процента выполнения от времени, можно найти зависимость величины процента выполнения от интенсивности и времени:
(6) g(t, у) = у(рр, у)) = g(W(y t / V),
и зависимость от интенсивности и времени размера вознаграждения, получаемого АЭ (см. выражение (1)).
Сделав маленькое отступление, отметим, что в [18] рассмотрена следующая задача. Пусть заданы доход центра и затраты АЭ, зависящие, в общем случае, от времени. Стратегией центра является выбор стоимости работ C 0 и шкалы оплаты ХР) из множества функций, удовлетворяющих введенным выше требованиям.
Он выбирает шкалу и сообщает ее АЭ, стратегией которого является выбор зависящей от времени интенсивности, которая, в свою очередь, в соответствии с выражениями (4)-(7) определяет продолжительность работ, динамику процента выполнения и выплат. Целью центра является максимизация дисконтированной разности между доходом и выплатами АЭ при условии, что АЭ (при известных ему стоимости работ и шкале) выбирает траекторию, максимизирующую дисконтированную разность между вознаграждением, получаемым от центра, и своими суммарными дисконтированными затратами.
Для этой задачи доказано, что, если функции дохода не зависят от времени и дисконтирование отсутствует (общий случай на сегодня не исследован), то, во-первых, при постоянной интенсивности оптимальное решение не зависит от шкалы и функции дохода центра (то есть в этом случае все шкалы эквивалентны), и, во-вторых, для любой переменной интенсивности работы АЭ найдется постоянное его действие, обеспечивающее ему ту же полезность. Последнее утверждение отчасти обосновывает рассматриваемый в настоящей работе случай постоянной интенсивности.
Синтез оптимальной шкалы при управлении проектом. Предположим, что центр должен компенсировать АЭ все затраты, которые он несет, участвуя в реализации корпоративного проекта. Тогда выполнено: C = V.
Проводимый анализ пока что не учитывал аспекты риска. Под риском будем понимать возможные потери участников проекта (УК и АЭ).
Запишем взятый со знаком минус баланс АЭ:
(7) fy, t) = y t - g(W(y t/ V)) C,
представляющий собой текущую разность между его затратами и компенсацией, выплаченной центром. Величина (7) характеризует риск АЭ - размер превышения затратами компенсаций (сколько ему недоплачивает центр в силу нелинейности функции W(-)). Очевидно, что у 0 fy, 0) = fy, V/y) = 0.
Как правило, величина (7) достигает максимальных значений на начальных этапах проекта.
Запишем взятый со знаком минус баланс УК:
(8) F(y, t) = [g(W(y t / V)) - W(y t/ V)] C,
представляющий собой текущую разность между компенсацией, выплаченной активному элементу и фактической (с точки зрения УК) стоимостью работ. Величина (8) характеризует в некотором смысле риск УК - размер превышения затратами УК на стимулирование фактической стоимости работ (сколько центр переплачивает АЭ в силу нелинейности функции W(-)). Очевидно, что y 0 F(y, 0) = F(y, V / y) = 0.
Как правило, величина (8) достигает максимальных значений на завершающем этапе проекта.
Так как исполнителю в итоге компенсируются все затраты (C = V), то будем считать, что он принимает решения, минимизируя риск, который будем оценивать максимальным по времени реализации проекта значением (7).
Обозначим множество интенсивностей, на которых достигается минимум риска при заданной шкале
(9) P(X0) = Arg min max f(y, t).
y0 te[0;V / y]
Пусть задано множество M допустимых (в рамках существующих институциональных ограничений) шкал. Тогда центр может искать шкалу, при которой время выполнения проекта будет минимально:
(10) min y ® max ,
yeP(/(-)) 7(-)eM
или шкалу, минимизирующую его собственный риск:
(11) max max F(y, t) ® min .
yeP(7(- )) te[0;V/y] g(-)eM
Рассмотрим примеры решения задач (10) и (11) для ряда практически важных частных случаев.
Утверждение 7. Если шкала оплаты является дифференцируемой функцией, то риски АЭ и центра не зависят от интенсивности, и определяются только шкалой ХО и функцией W(- ). Кроме того, если линейная шкала является допустимой, то она является решением задачи (11).
Доказательство утверждения 7. Последняя часть утверждения очевидна (см. выражение (8)). Для доказательства первой части найдем множество (9). В силу введенных предположений о свойствах функции W( - ) и шкалы множество времен, на которых достигается максимум выражения (7) определяется условием первого порядка:
= У - g'(W(y t / V)) W'(y t/ V) y = 0. ot
Решение последнего уравнения имеет вид: y t / V= F(W(-), XO), то есть является функционалом от функции W(-) и шкалы. Подставляя в (7) и (8) получаем, что риски, соответственно, АЭ и центра, не зависит от интенсивности y. Утверждение 7 доказано.
Рассмотрим три примера.
Для линейной шкалы f(y, t) = y t - C W(y t / V). Дифференцируя, получаем что максимум по времени достигается при (из двух времен, при которых производная функции W(-) равна единице, выбираем минимальное) t = t (y) = V W-1(1) /y.
Подставляя в целевую функцию (7) и обозначая d = fy, t (y)):
(12) d = V [W‘~1(1) - W(W‘-1(1))\ получаем, что она не зависит от интенсивности.
Для степенной шкалы (g(f) = ffа и W(z) = zb, а + b 1) f(y, t) = y t - V (y t / V)a+b. Дифференцируя, получаем что минимум по времени достигается при t* = T(y) / (а + Ь)1/а+ь-1.
Подставляя в целевую функцию:
М t*(y)) = V/ (а + b)1/a+b-1 [1 - 1 / (а + b)\, получаем, что она не зависит от интенсивности.
Рассмотрим третий пример, иллюстрирующий свойства S'-образных шкал. Пусть функция W(-) линейна, объем работ V = 1, а g(f) = 2 f2 / (1 + ffl).
Тогда максимум выражения (7) достигается при y t = 0.25371 f’ (а минимум выражения (7) и, соответственно, максимум выражения (8) - при y t = 0.7898) - см. рисунок 13.
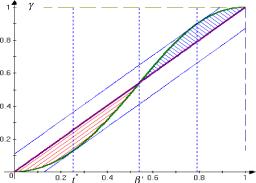
Максимальный риск АЭ (7) при этом равен 0.13, а максимальный риск центра (8) - 0.108.
Вернемся к анализу рисков центра и АЭ. В соответствии с утверждением 7, при использовании линейной шкалы риск центра равен нулю, а риск АЭ определяется выражением (12).
Риск АЭ равен нулю при условии (см. выражение (7))
(13) Х-) = W- (- ).
Если выполнено (13), то из (8) получаем, что риск центра равен:
(14) D = max [g(W(y t/ V)) - W(y t / V)] V.
te[0;V / y ]
С учетом (13) получаем, что D = S. Таким образом, мы обосновали справедливость следующего утверждения.
Утверждение 8. Для любой функции W( - ) максимальные гарантированные риски центра и АЭ равны.
С содержательной точки зрения линейная шкала, минимизирующая риск для центра, настолько же рискованна для АЭ, насколько для центра рискованна шкала (13) минимизирующая риск АЭ. Следовательно, целесообразно ограничиться рассмотрением шкал оплаты, лежащими в диапазоне между двумя этими предельными шкалами.
Данный диапазон может интерпретироваться как область компромисса - конкретная шкала (распределение риска между центром и АЭ) может получаться в результате переговоров в зависимости от последовательности принятия решений [43], при использовании того или иного механизма принятия решений [23, 40, 43] и т.д.
Оптимальные шкалы в управлении программой. Обсудим возможные обобщения полученных выше результатов постановки и решения задачи синтеза шкалы на случай реализации корпоративной программы.
Так как корпоративная программа включает несколько взаимосвязанных корпоративных проектов, то необходим учет рисков УК и активных элементов, выполняющих работы по корпоративным проектам.
Риск каждого из АЭ полностью определяется рассмотренной выше моделью, поэтому рассмотрим риски УК. Выделим два способа определения рисков УК в предположении их независимости. Первый - суммирование рисков по всем корпоративным проектам без учета их взаимосвязи и последовательности выполнения.
Второй (с учетом взаимосвязи и последовательности выполнения корпоративных проектов) заключается в вычислении максимума по времени реализации всей корпоративной программы суммы рисков по проектам, выполняемых параллельно в рассматриваемый момент времени. Остановимся на втором подходе более подробно.
Можно выделить две проблемы - определение набора шкал оплаты, минимизирующего риск УК, и унификация шкал оплаты. Особое внимание во втором случае следует уделять тому, что использование единой зависимости выплат от процента выполнения существенно снижает информационную нагрузку на УК и ставит АЭ в равные условия, но, в то же время, может увеличивать риск (так как унифицированная шкала является частным случаем набора персонифицированных).
Задача УК заключается в поиске разумного компромисса между этими двумя противоположными тенденциями.
Пусть УК использует персонифицированные (в общем случае различные для каждого АЭ) шкалы оплаты. Тогда в соответствии с выражением (12) риск УК при реализации /-го проекта равен
(15) 8/ = V/\w;-1(1) - WlWrXm, i е I,
где I = {1, 2, n} - множество проектов, n - число выполняемых
одновременно в рассматриваемый момент времени проектов.
В соответствии с (13) функция W(-) определяется шкалой g('), и наоборот. Обозначим M’ - множество функций W(-), таких, что с учетом (13) шкалы принадлежат допустимому множеству M. Тогда задача синтеза шкал в управлении программой заключается в нахождении набора шкал {W} еI, минимизирующего сумму рисков УК:
(16) X V/ \W/'-1(l) - W/(W/'-1(l))] ® min .
f~I {WQeM'}^
Если W(') - параметрически заданные функции, то (16) является стандартной задачей математического программирования.
Задача синтеза унифицированной шкалы, минимизирующей, риск УК, имеет вид: