Топологические методы в теории коллективного выбора
Это приведет к переходу от Q j к новому множеству
приоритетных потребителей Qj+1, соответствующему (j +1) шагу и т. д. Такая процедура сойдется к тому, что элементы будут либо получать x* = ri, (i е Q ), либо сообщать s* = D (j ? Q) и получать x}- rj.
Теорема 1.4.5 [80,89]. Для любого механизма распределения ресурса существует эквивалентный механизм ОУ.
Рассмотрим обобщения задачи существования эквивалентного прямого механизма. Обозначим через g. (s) произвольную процедуру
планирования, s. е S., s е S = П S. . Планы, назначаемые элементам
ІеІ
x = (Xj, ..., xn) е X = g( S). Будем считать, что функции полезности элементов однопиковые. Вектор точек пиков обозначим через
Г = Оі, ..., Гп ) [110].
Обозначим
Gi = {j е І: s е S, g (s) не убывает по s.},
Ht = {j е І: s е S, g (s) не возрастает по si} .
Введем следующие предположения (утверждения для квазиоднопиковых функций будут обозначаться ' , а результаты для них - приводиться в круглых скобках).
А.1.4.4. (А. 1.4.4’) І е І, Si = [di, Di ] с R1, - ? d1 D. +? .
А1.4.5. s е S, і е І g. (s) - строго возрастающая функция по s..
А.1.4.5’. s е S, і е І g. (s) - неубывающая функция по s..
А.1.4.6. (А. 1.4.6’) І е І, Gi - Нг = І.
А.1.4.7. (А. 1.4.7’) І е І, г е Rn и ~ е R1 если gi (s* (~ , Г-г)) gi (s* (г )), то
j е Gi gj (s* (~, Г-г)) gj (s* (г)) ,
j е Нi gj (/ (~г, P-i)) ? gj (s* (Р)) .
А.1.4.8. i е І, j е SP.
А.1.4.9. р ? X .
А.1.4.10’. P - X = 0 .
А.1.4.11’. Для любого i е І, для любых s-i е S-г, sj, s.2 еSi, sj s.2
если g(s1, s-.) г(гг+), g(s2, s-i) p.(p-), то АЭ сообщит s1; если g (s1, s-.) г (Г+), g (s2, s-i) r (r[ ), то АЭ сообщит s1; Структуру равновесия определяет следующая Лемма 1.4.3 [111]. Если выполнено А.1.4.4,1.4.5,1.4.8 (А1.4.4’,
A.1.4.5',A.1.4.8',A.1.4.10'), то для любого г е Rn ( г с Rn), для любого
i е І
1(1' ). Если g. (s* (г)) Г (Г-), то s* (г) = D.;
2(2'). Если g. (s*(р)) Рг (р+), то s*(r) = d. ;
3(3'). Если 5*(r) ? (dt, Dt), то gt(s*(r)) = rt(e [rt , r+ ]).
Следующие леммы определяет свойство соответствующего g (s) прямого механизма h(r), аналогичное бескомпромиссности в [5,40] и §2 главы I.
Лемма 1.4.5 [111]. Если выполнено А.1.4.4,1.4.5,1.4.8 (А1.4.4’,
A.1.4.5',A.1.4.8',A.1.4.10'), то для любого r e Rn (r c Rn), для любого
i ? I
1. Если h (r) ri, то h (r), h (~, r_i) = h (r);
2. Если hi (p) pt, то hi (r), hi (~, r_i) = hi (r).
Лемма 1.4.6 [111]. Если выполнено А.1.4.4,1.4.5,1.4.8 (А1.4.4’,
A.1.4.5',A.1.4.8',A.1.4.10'), то для любого p e Rn (rc Rn), для любого І ? I
1. Если h (p) pt, то V~ h (r), h (~, r) h (r);
2. Если h (r) r, то h (r), h (~, r) h (r).
Следующая теорема дает достаточные условия существования
эквивалентного прямого механизма.
Теорема 1.4.6 [111]. Если выполнено А.1.4.4-1.4.10 (АЛ.4.4,-AЛ.4ЛГ), то для любого механизма существует эквивалентный прямой механизм.
Эта теорема обобщает теоремы 1.4.5 - 1.4.6, но не удобна для практических целей, поскольку проверка её условий требует вычисления равновесных сообщений и равновесного распределения планов при каждом профиле предпочтений активных элементов.
В настоящем параграфе мы рассмотрели один из способов построения механизма достоверно реализующего заданное СГВ. При этом, для механизмов частного вида (механизмы активной экспертизы и распределения ресурса) были получены конструктивные условия (накладываемые на непрямые механизмы) достаточные для существования эквивалентных прямых механизмов (Т.1.4.2, 1.4.3).
Для механизмов планирования общего вида построить удобные и конструктивные, с точки зрения проверки, условия существования эквивалентного прямого механизма не удалось и на текущий момент подтверждение существования эквивалентного прямого механизма (согласно условиям АЛЛА^ЛА^) требует вычисления равновесия Нэша для каждого возможного профиля предпочтения (Т.1.4.5).
В следующем параграфе мы рассмотрим результаты применения топологических методов для исследования задач коллективного выбора.
§5. Топологические методы в теории коллективного выбора
Исторически, наиболее ранние методы исследования проблем теории коллективного выбора формулировались в предположении дискретности (конечности) множества возможных альтернатив A, и предпочтения АЭ при этом представлялись бинарными отношениями. Такая формулировка накладывает определенные ограничения на методы исследования проблем коллективного выбора, связанные с дискретными методами, описанными в §§ 3-4 настоящей работы.
В частности формализм бинарных отношений предпочтения неудобен при исследовании механизмов голосования, описанных в § 2 настоящей главы, а механизмы, используемые в дискретных теориях, являются достаточно громоздкими.
Однако, наиболее часто, в задачах теории коллективного выбора множество возможных альтернатив непрерывно, что дает возможность использовать топологические методы исследования задач теории коллективного выбора. Применение топологических методов позволяет исследовать не только стандартные проблемы теории коллективного выбора [13,15-19], но и неманипулируемость правил коллективного выбора [14,60], а так же исследовать механизмы коллективного выбора с бесконечным числом АЭ.
Как отмечалось в § 2 главы I результаты о невозможности Эрроу тесно связаны с проблемой неманипулируемости механизмов планирования, а так же с ограничениями множеств возможных предпочтений АЭ, необходимых для того, чтобы в активной системы существовала возможность построить неманипулируемый механизм планирования.
Применение топологических методов анализа проблем коллективного выбора показывает, что существование ФКА, удовлетворяющей НПАА и ПО эквивалентно существованию непрерывного симметричного отображения из произведения единичных сфер на единичную сферу и связано с теоремой Брауэра о неподвижной точке. Теорема о невозможности в топологической формулировке выглядит следующим образом.
Обозначим П - пространство непрерывно дифференцируемых функций полезности над евклидовым пространством возможных альтернатив. По аналогии с механизмами голосования § 2 главы 1, ФКА 3: Пп ® П назовем анонимной, если для любого профиля P е Пп и для любой перестановки p множества I выполняется 3(Pj, P2,..., Pn) = 3(Pp1, Pp2,..., Ppn). Единогласной назовем ФКА 3: Пп ® П, такую, что для любого профиля предпочтений P е Пn, такого, что для любых АЭ i, j е I Pi = Pj выполняется 3(P) = Pk для любого к е I.
Теорема 1.5.1 [5,63,17]. Не существует ФКА 3: Пп ®П, удовлетворяющей условиям непрерывности (в смысле равномерной метрики), анонимности и единогласности.
Таким образом, при достаточно общих предположениях не удается построить отличного от диктаторского механизма коллективного выбора и/или функции коллективного агрегирования, и для того, чтобы существовал недиктаторский механизм коллективного выбора, необходимо изменить условия, налагаемые на механизм коллективного выбора. Как показывалось в § 3 при усложнении множества возможных сообщений АЭ удается найти механизмы, в которых активные элементы сообщают достоверную информацию, однако в таких механизмах потребуется изменение определения неманипулируемости в связи с тем, что сообщением АЭ уже не будет информация только о своих предпочтениях.
Другая возможность построения неманипулируемых механизмов коллективного выбора заключается в изменении множества допустимых предпочтений. В частности, в § 2 рассмотрены неманипулируемые механизмы голосования.
В рамках настоящей работы нас будут интересовать результаты применения топологических методов для исследования неманипулируемости механизмов коллективного выбора [14].
Пусть п - количество активных элементов, множество
возможных альтернатив A = Rm+, предпочтения АЭ заданы
m
однопиковыми функциями полезности вида ji(x) = -^aj(Xj -rj) , где
j=i
aj 0, j = 1, m , i е I, r е A - точка пика функции полезности. Множество возможных сообщений каждого АЭ S, определяется либо как S = Rm+, либо S = Rm.
Функцию f: Rn ® R назовем локально постоянной либо
диктаторской (ЛПД) [14], если она непрерывна, и для почти всех r е Rm существует окрестность U (r) такая, что для всех Г е U(г) либо f (T) = const, либо существует АЭ d , такой, что f (T) = rd.
Функцию f :(Rm)n ® Rm назовем сепарабельной если
f oi\m,c)rn),fm (rm,rm)).
Функция f :(Rm)n ® Rm называется покоординатно ЛПД если она сепарабельна и для каждого к = 1, m, функция fm удовлетворяет ЛПД.
Основной результат работы [14] представляется следующей Теорема 1.5.2 [14]. Механизм g: Sn ® A неманипулируем тогда и только тогда, когда он удовлетворяет ЛПД.
Таким образом теорема 1.5.2 утверждает, что любой неманипулируемый механизм состоит из множеств, в которых определенные АЭ являются диктаторами, то есть механизм g назначает
наилучший для них результат. При этом, из теоремы 1.5.1 следует, что любой неманипулируемый механизм вида g : Sn ® A непрерывен. Таким
образом, результаты работы [14] являются топологической интерпретацией результатов работ [14, 53], обсуждавшихся в § 2.
Топологический подход также позволяет рассмотреть вопрос об устойчивости неманипулируемых механизмов вида g : Sn ® A . Будем считать, что множество возможных альтернатив A является кубом Im в Rm , множество возможных сообщений каждого АЭ так же является кубом I m в R m . Таким образом, все неманипулируемые механизмы вида g : Imn ® Im принадлежат множеству C0(imn, Im) непрерывных отображений из Imn в Im. На множестве C 0(Imn, Im) введем расстояние между элементами f и g следующим образом d(f, g) = sup |f (x) - g(x)\. Справедлива следующая
XGImn
Теорема 1.5.3 [14]. Множество манипулируемых механизмов на
ограниченном множестве возможных альтернатив является всюду плотным множеством в пространстве C 0( Imn, Im).
Таким образом, малые изменения неманипулируемого механизма могут оказаться манипулируемыми.
Другой проблемой, которую удается решить применением топологических методов, является исследование механизмов с бесконечным количеством элементов [20].
Теорема 1.5.4 [20]. Существует непрерывная ФКА для бесконечного числа АЭ, которая удовлетворяет свойству Парето, единогласности и не является диктаторской, и определяется как предел диктаторских ФКА.
При этом, ФКА, определенная в работе [20], может не быть анонимной, однако удовлетворяет условиям непрерывности, единогласности и условию Парето, кроме этого, ФКА, определяемая теоремой 1.5.4, удовлетворяет усиленной версии независимости от посторонних альтернатив [20]. Возможны и другие подходы к решению проблемы бесконечного числа АЭ, в частности поиск ФКА, удовлетворяющих НПАА и не являющихся диктаторскими [25,45].
Таким образом, топологический подход позволяет значительно упростить решения части проблем теории коллективного выбора и построить эквивалентные топологические интерпретации других.
§6. Постановка задачи исследования манипулируемости механизмов планирования
В предыдущих параграфах приведены известные условия неманипулируемости для механизмов планирования и условия реализуемости СГВ. Также мы рассмотрели механизмы планирования частного вида, для которых было доказано существование эквивалентного прямого механизма.
Для механизмов планирования общего вида были проанализированы достаточные условия существования эквивалентных прямых механизмов, однако эти условия недостаточно конструктивны, так как требуют поиска равновесия для каждого возможного профиля предпочтений.
Таким образом, возникает необходимость построения конструктивных достаточных условий неманипулируемости механизмов планирования. Далее определим классы активных систем и механизмов планирования (прямых и непрямых), исследуемых в настоящей работе.
Обозначим /={1,..., п}множество всех АЭ, xi еR1 план i-го АЭ. Планы АЭ назначаются по сообщениям АЭ s) е Si, i е I: xi = gi (s).
Функция полезности i -го активного элемента - ji (x) называется сепарабельной, если она зависит только от плана, назначаемого i -му элементу, то есть ji (x) = ji (xi). Функция полезности ji (xi) является
обобщенно однопиковой, если существует точка r е R1 такая, что ji (r) ji (xi) при любых xi Ф r и ji (xi) не убывает по x до точки r и не возрастает после неё. Точка r называется точкой пика или идеальной точкой.
Класс всех обобщенно однопиковых функций обозначается GSP и, очевидно, содержит класс однопиковых функций SP.
Всюду ниже, если не оговорено особо, предполагается, что полезность АЭ не трансферабельна, а АЭ имеют обобщенно однопиковые, сепарабельные функции полезности.
В дальнейшем, рассматривая прямые механизмы планирования, будем предполагать, что элементы сообщают не свои предпочтения (то есть функцию полезности), а только идеальные точки своих функций полезности. Такие механизмы являются устойчивыми к конкретному виду функций полезности при условии, что они остаются обобщенно однопиковыми.
Набор функций полезности всех элементов (j1,..., jп) обозначим через j . Вектор точек пиков всех элементов (r1,...,rn) е Rn обозначим через r. Вектор точек пиков для профиля предпочтений j е GSPn будем записывать как r = peak (j).
В прямых механизмах элементы сообщают оценку положения своих точек пиков из R1, таким образом, в прямых механизмах множество возможных сообщений каждого элемента есть R1. Пусть элементы посылают в центр сообщения ~ е R1.
План i-го элемента определяется процедурой планирования hi(~), где ~ = (~, ..., ~) е Rn. Обозначим вектор планов через х = (х1, ..., xn) е Rn. Механизм планирования будет определяться множеством возможных сообщений Rn и процедурой планирования h:Rn ® Rn .
В непрямых механизмах планирования множества возможных сообщений каждого АЭ i е I представляют собой отрезки действительной оси. Без ограничения общности будем считать, что Si = [0,1]. Таким образом, процедура планирования в непрямом
механизме представляет собой отображение g : S ® Rn .
Как отмечалось ранее, будем рассматривать такие механизмы, в которых каждый АЭ сообщает только свою точку пика ri е R1 , и, следовательно, множество возможных сообщений всех АЭ - все Rn , при этом процедура планирования будет отображением h: Rn ® Rn . Под достоверной информацией будем понимать реальное положение точек пиков элементов. Прямой механизм планирования называется неманипулируемым, если для любых идеальных точек АЭ сообщение достоверной информации является равновесием в доминантных стратегиях, то есть V j е GSPn, r = peak(j) и УiеI, ri е R1, r_i е Rn-1 выполнено
jt (hi (ri, r_i)) j (hi(r, r_t)).
Таким образом, первой задачей настоящего исследования можно считать поиск условий на прямые механизмы вида h: Rn ® Rn, являющиеся достаточными для его неманипулируемости.
Пусть механизм g: S ® Rn не является прямым и для каждого
профиля предпочтений j е с SPn мы знаем одно из положений равновесия s* (j) которое зависит только от положения точек пиков элементов r е R n . Такие равновесия будем записывать следующим образом: s’*(r).
Для непрямого механизма g : S ® Rn построим соответствующий ему прямой механизм следующим образом. Элементы сообщают информацию ~ е R1, i е I о своих точках пика, центр по ним находит
вектор равновесных заявок s* (r) для механизма g : S ® Rn и назначает планы х = g(s* (r)). Получим новый механизм h(r) = g(s* (r)).
Если соответствующий прямой механизм h(r) неманипулируем, то для непрямого механизма g: S ® Rn существует эквивалентный прямой механизм h(r) = g(s* (r)).
Таким образом, второй задачей настоящего исследования является поиск условий на исходный непрямой механизм G = (S, g),
являющихся достаточными для того, чтобы положение равновесия зависело только от точек пика АЭ, и соответствующий прямой механизм был неманипулируем.
Так как условия существования эквивалентного прямого механизма накладываются на исходный непрямой механизм, то появляется возможность исследовать влияние изменений исходного непрямого механизма на существование эквивалентного прямого механизма. Поскольку менять процедуру планирования обычно не представляется возможным, актуальной является третья задача - задача анализа влияния множества допустимых сообщений на существование эквивалентного прямого механизма.
Как было показано в обзоре, приведенном в §§ 1-5 настоящей главы, существует множество подходов к исследованию неманипулируемости. В то же время, достаточно перспективным, с точки зрения получения условий неманипулируемости механизмов планирования, выглядит подход, предложенный в [7,94-96], который развивается в настоящей работе.
Таким образом, изучение условий неманипулируемости
механизмов планирования можно свести к следующим задачам:
- получение условий неманипулируемости прямых
механизмов;
- получение условий существования эквивалентных прямых механизмов;
- исследование влияния множества допустимых сообщений на существование эквивалентного прямого механизма.
Решение этих задач приводится соответственно в главах II и III.
Глава II. Условия неманипулируемости прямых механизмов планирования, сформулированные в терминах множеств диктаторства
В предыдущей главе мы рассмотрели постановку задачи поиска неманипулируемого механизма планирования и основные проблемы, возникающие при исследовании неманипулируемости. При анализе манипулируемости механизмов планирования будем исследовать их множества диктаторства, определяемые ниже.
В первом параграфе приведены основные определения, необходимые для исследования множеств диктаторства прямых механизмов планирования и достаточные условия неманипулируемости прямых механизмов планирования в терминах множеств диктаторства. Во втором параграфе приведены необходимые и достаточные условия коалиционной неманипулируемости прямых механизмов планирования. В § 3 исследуется неманипулируемость механизмов с векторными планами.
В четвертом параграфе приводятся свойства механизмов активной экспертизы и распределения ресурса, описанных в главе I, с точки зрения метода исследования множеств диктаторства.
§1. Множества диктаторства и неманипулируемость прямых механизмов
Рассмотрим прямой механизм h : Rn ® Rn. Пусть для некоторого сообщения ~ е Rn выбирается вектор планов х = h(~). Так как
полезность каждого АЭ определяется однопиковой функцией полезности, то каждый АЭ может находиться в одном и только одном из трех возможных состояний: (а) либо hi (~) ~ и тогда АЭ будет получать план,
строго больший желаемого, (б) либо h (~) = ~ и АЭ будет назначаться оптимальный для него план, (в) либо h (~) ~ и план будет
недостаточным. Для каждого активного элемента i е I введем индекс состояния, принимающий значения из набора {a, c, ш}=р, где a соответствует состоянию (а), ссостоянию (б), а ш(в), и обозначим его через pi (символы индекса являются первыми буквами фр. слов manqueнехватка, contentementудовлетворенность, abondance избыток).
Вектор индексов состояния всех АЭ обозначим через ре pn.
Введем соответствия M:pn®21, C:pn®21, ^:pn®2I, значениями которых для каждого вектора состояний ре pn будет подмножество АЭ из I, таких, что индексы состояний этих элементов равны, соответственно, ш,
c и a: M(p)={jeI: Pj=m}, C(p)={jeI: Pj=c}, A(p)={jeI: Pj=a}, pepn. Очевидно, для каждого p подмножества C (p), A(p), M (p) в
совокупности являются разбиением множества всех элементов I. Определение 2.1.1. Разбиением B пространства Rn назовем совокупность множеств DpcRn, таких, что
Dp = {~ еRn| hi(~) ~ если i еM(p), hi(~) = ~ если i е C(p) и hi (~) г, если i е A(p)}, p е pn.
Сокращенно неравенства hi (~) ~, при i eM(p) будем записывать hM(p)(~) ~M(p), а неравенства ht(~) ~, при ieA(p) как hA{p)(~) ~i(p). Как видно из определения, для каждого множества Dp разбиения B задано множество элементов C (p), называемых диктаторами, которые получают оптимальные планы, остальные элементы при этом получают некоторые неоптимальные для себя планы. Разбиение B назовем разбиением на множества диктаторства, а сами множества Dp -
множествами диктаторства.
Далее будем предполагать, что в каждом из множеств Dp разбиения B планы, назначаемые всем активным элементам зависят только от сообщений диктаторов C (p) в этом множестве и не зависит от
сообщений остальных элементов, если вектор сообщений ~ находится в этом множестве. То есть, существует функция хp(~(p)), определенная на для всех ~ ( ) е ProjC(p) Dp , такая, что для всех ~ е Dp выполняется h(~) = xp (~C (p)) и выполнено предположение
А.2.1.1. Для всех pe pn существует функция
хp : ProjC(p)Dp ® Rn, такая, что r е Dp выполнено h(~) = xp (rC(p-,).
Содержательно предположение А.2.1.1 означает, что планы, назначаемые для всех векторов сообщений из одного и того же множества диктаторства, не зависят от сообщений АЭ, не являющихся диктаторами. Предположение А.2.1.1 будем считать выполненным, если не оговорено особо, в ходе всего последующего изложения.
Введенные определения иллюстрируются следующим примером.
Пример 2.1.1. Для механизма g1 (5) = s1 + 2 - s2, g2 (s) = + s2,
si е [0, 1], i = 1, 2, (?1, r2) е R2 рассмотрим соответствующий прямой
механизм. Он задается следующими соотношениями:
x(cc)(r1, r2) = (r1, r2), при
01, r2) 6 D(c, c) = {(гг, r2): 2 - r2 -1 r 2 - r2, rx -1 r2 r\};
x(c,m)(n) = (ri,n), при (ri, r2) e % m) = { (ri,r2): r 6 [0, 1], r2 rj2 };
x(c a)(ri) = (ri, Гі -1) , при (ri, r2) 6 D(c, а) = { ri 6 [2, 3], r2 (ri +1)/2 };
x(m’ c)(r2) = (1 - 2 - r2 , r2 ) , ПРИ (rU r2) 6 D( m, c) = { r2 6 [1, 2] , r1 1 + r2 }
x(a’ c)(ri) = (2 - r2, r2), при (ri, r2) 6 D(a^ c) = { ^ 6 [0, 1], ri r2 };
x(m m) = (3, 2), при (ru r2) 6 D(m, m) = { r1 3, r2 2 };
x(m, a) = (1, 1), при 0i, r2) 6 D(m, a) = Vi 2, ^ 1}- {^ 6 (1, 2], r2 2- Гі} ;
x(a, m) = (2, 1), при ^ r2) 6 D(a, m) = {ri 1, Г2 1} - fa 6 [1, 2), Г2 2 - Гі - 1};
x1^ a) = (0, 0), при (Гі, r2) 6 D( a, a) = { Гі 0, Г2 0 }.
Легко проверить, что - Dp = R2 и Vp1 Ф p2, D 1 - D 2 =0 , то есть B
P6p2
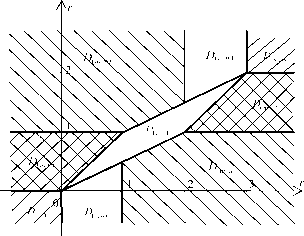
есть разбиение R2. Множества разбиения изображены на рис. 2.1. -
Определение 2.1.2. Определим совокупность множеств
Dp, ={r6R: rM(p) xM(p)(rC(p)) , rC(p) = Proj C(p) Dp, rA(p) xA(p) (rC(p)) }, p6pn.
Из определения 2.1.2 очевидно, что для любого p 6pn выполнено включение Dp ^ Dp . Так же очевидно, что если для любого вектора сообщений ~ 6 D( выполняется h(r ) = xp (~(p)), то для любого вектора истинных точек пика r 6 Dp сообщение достоверной
| информации является наилучшим сообщением из D для всех АЭ. Пример 2.1.2. Для примера 2.1.1 множества совокупности |
|||||||||||||||||||||||||||||
|
D(C, m) = {r e R: Г1 e[2, 3]. Г2 1 + Г2};
Dla, m) = {Г e R': Г1 2. Г2 1};
D(0a, c) = {Г e R: Г2 e[0, 1]. Г1 2Г2};
K. c) = D(c, c) по определению.
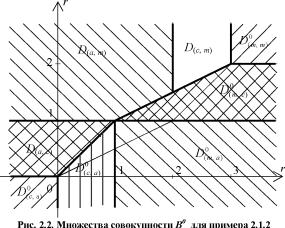
ножества D, a) . D , a) . D(0m, a) . ^ c) . D^ m) изображетЫ на рис.
2.2.-
Свойства множеств из B0 иллюстрируются следующей леммой. Лемма 2.1.1. Рассмотрим произвольный re D0p , тогда:
a) VieM(p) { (~,r-) e D0p} xp(rc(p)) }, (2.1.1)
б) ieR(p) {(~,r-) е D?} {~ x?(rc(p)}. ^ 2) (2.1.2)
Под записью B=B0 будем подразумевать, что p ер, Dp = D? .
Теорема 2.1.1. Пусть I - множество активных элементов, функции полезности которых обобщенно однопиковые. Пусть механизм h: R ® R удолетворяет А.2.1.1 и B=B0 , тогда он неманипулируем. ^ Очевидно, условия теоремы 2.1.1 не выполнены в примере 2.1.1. Механизм примера 2.1.1 оказывается манипулируемым.