Существование эквивалентного прямого механизма
Rn . ^
Следующим утверждением устанавливается свойство малых окрестностей точек в Rn по отношению к разбиению {Sp}^ ^n : для каждой точки s e Rn существует набор
/К
s1
Рис. 3.1
есть разбиение
Утверждение 3.2.1. Совокупность множеств
{SP}pepn
определяемый множеством их векторов
множеств разбиения {Sp}
состояний p0(s) такой, что все достаточно малые окрестности точки s пересекаются только с множествами Sp, р ер0 (s).
Утверждение 3.2.2. Для любого s e Rn существует множество векторов состояний 0 ^ р0 ср и число ?0 0 такие, что
e e (0, ?0), р ер0, UE (s) - Sp Ф0 и р гр,, 0 (s) - Sp Ф0 . ^
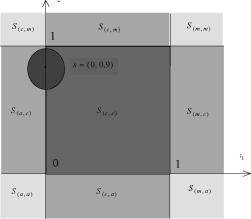
Пример 3.2.2. Поясним это утверждение на следующем примере (см. рис.
3.2). Рассмотрим точку s е R2, s = (0, 0,9) и окрестность радиуса 1,5 . Эта окрестность будет пересекаться со всеми множествами разбиения {Sp }ре^„. Окрестность радиуса 1 будет пересекаться только со
множествами S(a, а S(C, а S(a, ф S(c, ф S(a, m S(c, m) . Окрестность радиуса 0,5 будет пересекать только множества S(а, c), S(c, c), S(а, m), S(c, m). А все
окрестности радиуса меньше 0,1 пересекаются только с двумя множествами S(a c), S(c c). Поэтому множество р0 для точки s = (0,0,9)
будет состоять из элементов р0 = {(a, c), (c, c)} .-
Далее докажем, что любой отрезок с началом не в S(c, c)
пересекается с внутренностью некоторого множества Sp, где
Р *{c,...,c}.
Утверждение 3.2.3. Пусть s1 Ф s2 e Rn. s1 e Sp1 и s2 e S^2 и
p1 Ф {c, ..., c}, тогда $a 0 и $p 'ep: t e (0, a) s(t) = s'(1 -1) + s2t e Sp, и p' Ф {c,..., c} . ^
Определим множества Qp = {s e Rn : sC(p) e Rc(ps-C(p) = spC( )} и
произвольные s1, s2 e Rn такие, что они принадлежат разным множествам разбиения {Sp }, то есть можно указать такие вектора p1, p2,
о1 Ф p2 что s1 e S , и s2 e S 2 .
p1 p2
Рассмотрим отрезок [s1, s2] = {s(t) = s1t + s2(1 -1), t e [0, 1]}. При p = {c, ..., c}, [s1, s2] c Qp = Rn.
Найдем множество p всех векторов из pn таких, что [s1, s2] c Qp, p ep. Обозначим
p'(s\ s2) = ArgmaxjI \ C(p)| .
pep
Поясним введенные определения на следующем примере.
Пример 3.2.3. Рассмотрим разбиение {Sp}pepn и отрезок [s1,s2],
где s1 = (-0,3, 1), s1 = (0,5, 1). Множества Qp будут следующими (см. рис. 3.3)
Q(c, c) = R2;
Q(m, m) = (1, 1) ;
Qa m) = (0, 1);
Q(m a) = (1, 0);
Q(a a) = (0, 0);
Q(c, a) = {r 6 R2 : S 6 (-?, + ?), s2 = 0};
Q(a, c) = {r 6 R2 : Si 6 (-?, + ?), S2 = 1};
Q(c, m) = {r 6 R2 : S2 = 0, S2 6 (-?, + ?)};
Q(c, c) и Q(c, m) .
этом
p'(s\ s2) состоит из
Q(m, c) = {r 6 R2 : S = 1, S2 = (-?, + ?)}. Тогда [ s1, s2 ] будет принадлежать
p(s\ s2) = {(c, c), (c, m)}. При
p'(s\ s2) = Argmax| I \ C( p)| = {(c, m)}.^
Утверждение 3.2.4. Vs1, s2 6 R2 множество одного элемента.
Единственный элемент р ер'обозначим р .^
Поскольку для каждого s е Rn существует единственный р еРп такой, что s е Sp, то однозначным будет следующее доопределение отображения g : S ® Rn на все Rn . Рассмотрим произвольный s е Rn , существует единственный р е pn такой, что s е Sp . В точке s определим функцию G(s) таким образом, что Gc(р)(s) = gc(р)(spc(р},sc(р)) и
G-C(p)(s) = g-c(р)(sc(рУ sC(р)) + (s-C(р) - s-c(р)) . ОчевиДно, если
s е S = [0, 1]n то G(s) = g(s).
Пример 3.2.4. Рассмотрим доопределение функции g : S ® Rn для механизма примера 2.1.1.
Если s е S(^ c), то g(s) = G(s).
Если р = (c, m), то c(р) = {1} и I \ c(р) = {2}, и s-cр = s2c, m) = 1. При этом G(s) для всех s е S(c, m) определится следующим образом:
G1(s)
G2(s)0 0 g2(sU 1)
s1 + 2
g1(s1,1) 0+f 0
s1 + 2
G(s) =
s2 1
sj + 1 + s2 - 10 I sj + s-
Если р = (c, m), то c(р) = 0 и s'm’ m) = fjj, a G(s) для всех
s е S(m, m) определится следующим образом:
G1(s) 0 = f g1(1, 1) 0 + fs1 -10 = f s1 + 2
G2(s ) 0 t g 2(1, 1)
При s е S(m, c), аналогично получаем:
G1( s)
s2 +1
g1(1, s2 ) ) + (s1 - s1 + 2s2
s2 +1
G( s) =
G2 (s)0 0g2(1, s2)0 00
Q(s) 0 f s,
При s е S(
G( s) =
(m, a)
G2 (s) 0 0 s2 + 1 Q( s) 0 = t s, G2(s)
При s е S
G( s) =
(c, a)
s1 + s2
Q(s) 0 f st
При s е S(a, a) , G(s) =
G2 ( s) 0 0 s2
Приведем некоторые свойства функции G, доказательства которых можно найти в приложении.
Лемма 3.2.1. Gt(s) не убывает по st для любых s ? Rn. ^
Лемма 3.2.2. G(s) непрерывна в Rn . ^
Лемма 3.2.3. Если g(s) непрерывна и частично монотонна, то для любого r ? Rn существует s ? Rn такой, что G(s) = r . ^
Лемма 3.2.3 позволяет доказать справедливость следующего утверждения о существовании и структуре равновесия.
Теорема 3.2.1. Пусть процедура планирования g: S ® Rn непрерывна в S и частично монотонна в S. Тогда для любого j ? GSPn с вектором точек пиков r ? Rn существуют равновесие Нэша s’*(r) и вектор состояний р ?pn такие, что s’*(r) = (spC(р),sC(р)), где sc(p) ?[0, 1]|C(P). при этом gc(p)(s*(r)) = rC(р), gM(p)(s*(r)) rM(r) и gA( p )(s* (r )) rA( p ). ^
Как видно из теоремы 3.1.1, положение равновесия для каждого профиля зависит только от вектора точек пиков и не зависит от конкретного вида функций полезности.
Таким образом, мы ввели разбиение пространства Rn на множества Sp и, используя это разбиение, доопределили процедуру
планирования g(s), s ? [0, 1]n на все Rn .
Это доопределение позволило нам доказать теорему 3.2.1 о существовании и структуре равновесия Нэша в механизме (S, g). В дальнейшем свойства, устанавливаемые утверждениями 3.2.1-3.2.3 и теоремой 3.2.1 понадобятся при построении достаточных условий существования эквивалентного прямого механизма.
§3. Существование эквивалентного прямого механизма
Перейдем к построению достаточных условий существования эквивалентных прямых механизмов.
Если задано отображение f: A ® B, то под записью f-1 будем
понимать соответствие f-1: B ® 2A , такое, что a е B выполняется
f (f _1(a)) = a .
Наложим на отображение g: S ® Rn и связанное с ним отображение G : Rn ® Rn, определенное выше дополнительные условия. А.3.3.1. Для любых r е Rn и для любых р ерп таких, что
гС(р) е gC(r )(s-C( р) [0, l]C(P )) соответствие g (s-c (р у gp(rC(p)))
однозначно.
Здесь g -1(-) обозначает обратное соответствие
g-1:gC(р)(spC(р), [0, 1]C(P^ ® [0, 1]C(р^ для р ерп: C(р) ^0 . Для р ерп таких, что C (р) = 0 и C(р) = I будем считать соответствие g (s-C ( р ) , gp(C(р))) однозначным по определению.
Условие А.3.3.1 гарантирует наличие функции xр (с (р)) определенной в § 1 главы II для соответствующего прямого механизма x р (rC (р)) = g (*рС (р у g C (р))).
Пример 3.3.1. Для механизма выполнение предположения А.3.1.1.
примера 2.1.1 проверим Рассмотрим р = (c, т).
Обратное соответствие
(sx + 2^|
? s1 +1 0
gc^-a р), sc( р)) = g(s1, 1)
gp\гс(р)) = g-, т)(г) для всех r е gj(1, [0, 1]) = [2, 3] задается выражением g(-c1, m)(r1) = r1 -2. Очевидно, что оно однозначно. Если р = (т, т), то С(р) = 0 и А.3.3.1 выполнено по определению. -
Определим вектор состояния M1 ерп для любого 1 е I таким образом, что С(M1) = I\{i} и M(M1) = {1} . Аналогично определим A1 е рп так, что C(A1) = I \{1}, A(A1) = {1}.
А.3.2.2. Для любых i e I, r_ e Rn 1 соответствие
соответствие
G(, G^ji (r_i)) однозначно и i e I, r_i e Rn 1
G(sA , Gj(r_)) однозначно, где G J : Rn 1 ® Rn 1 и G J : Rn 1 ® Rn 1 обозначают обратные соответствия для G_ (sM , s_;-) и G_ (sj , s_;-).
и Gj : Rn_1 ® R
То, что соответствия G . 1: Rn 1 ® Rn
определены на всем Rn 1 доказывается аналогично лемме 3.2.3.
Условие А.3.3.2 и определяемое ниже условие А.3.3.3 позволяют гарантировать совпадение совокупностей D и D0 .
Пример 3.3.2. Для механизма примера 2.1.1 проверим выполнение
предположения А.3.3.2. M1 = (m, c), M2 = (c, m), A1 = (a, c),
A2 = (c, a).
S2 1;
s2 +1 2s2 +1 1 + s2
1
s2 +1 0 '
G(s1M 1, S2) = '
S2 e [0, 1]; S2 0., S2 0;
^2
'2s.
G(sj , S2) = \
s2 e[0, 1];
G ,J: R1 ® R1 будут
Обратные соответствия G_ 11 : R1 ® R1
M A
определяться следующими выражениями G^^) = Г2_1 и GjJ^) = Г2
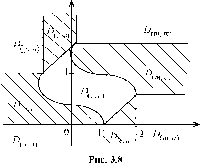
для всех r2 e R1. Графики соответствий G(sM , GM[1(r2))
G(s^A ,G41 (Г2)) изображены на рис. 3.4 с обозначениями M1 и A1 соответственно, а сами соответствия определяются выражениями:
' 3 ,
Г 2;
G(sf , G-1i(r2)) =
M
Г2 6 [1, 2];
Г2 1;
r2
r2 0;
, Г2 6[0, 1];
2r2
G (s^, G^))
22
, r2 1.
2 2
Аналогично соответствия G(Sf , G-^^)) и G(s2 , G^-2(ri))
2 2
изображены на рис. 3.5 с обозначениями M и A и задаются выражениями
Г2 3;
G(sM , G-\(Г2)) = M
Г2 6 [2, 3];
ri -1 Г1
Г2 2;
r i;
Г2 e[0, i]; -
Г 0.
А.3.3.3. для любых i e I и для любых s: st e [0, i] выполняется
Gi (sfM , GM[i (GC(Mi)(s))) - Gi(s) - Gi(sA , GA1 (GC(Ai)(s))).
Условия А.3.3.2 и А.3.3.3 позволяют гарантировать совпадение совокупностей D и D0 .
Пример 3.3.3. Очевидно, оба неравенства:
G2(sM , GM12(GC(M2)(s))) - G2(s) - G2(s2 , GA2(Gc(A2)(s))) и
G[(sM 1, G^i (GC (M i)(s))) - G[(s) - G[(s[A, G^[ (Gc (Ai)(s))) не выполняются, например, в точке s = (0.5, 0.75), G(s) = (1.75, 1.25). Так G[(sM[,G~Mi (GC(M[)(s))) = 1.5 G[(s) = 1.75 и
G[(s) = 1.75 G1(s1A1,GAL (Gc(Аь )(s))) = 2 ;
G2(sM , GM12(GC(M2)(s))) = 1 G2(s) = 1.25 (см. рис. 3.6 и 3.7). -
Далее покажем, что введенные условия А.3.3.1 - А.3.3.3 достаточны для существования эквивалентного прямого механизма.
Соответствующий прямой механизм будет характеризоваться своими B -
разбиением и B0 совокупностью. Теорема 3.2.1 позволяет для соответствующего g(s) прямого механизма определить совокупность B0
множеств dJ с Rn , p epn таких, что
DP = {r e Rn : rc(p) = gc(r)(spc(р^ [0, 1]C(P^
rM(p) xM(p)(rC(r)), rA(p) xA(p)(rC(r))}. Лемма 3.3.1. Пусть выполнено А.3.3.1, тогда p epn,
D0 = G (S p). ^
Приведенная лемма 3.3.1 показывает, что при условии А.3.3.1 множества совокупности D0 являются образами множеств совокупности
Sр при отображении G: R" ® Rn.
Лемма 3.3.2. Пусть выполнены условия 3.3.1-3.3.3, тогда для любого i е I справедливы
а) р ер": i е M (р)г е Dp выполняется ri Gi (sIM , G__ji (r_i)),
б) р ер" : i е C( р ),r е Dp0 выполняется
G, (sM', G-У (r_i)) r G, (sf, Gf1 (r_i)),
в) p ер" : i е f( p), r е Dp0 выполняется Gi (sf , Gf1 (r_t)) rt . ^
Теорема 3.3.1. Пусть для всех элементов функции предпочтений (рi е GSP. Пусть g (s) непрерывна и частично монотонна в S и выполнены предположения А.3.3.1-3.3.3, тогда верны следующие утверждения:
1) Существует выбор равновесия s* : R" ® S такой, что для каждого r е R", s*(r) -равновесие Нэша в механизме g: S ® R" и для любых р ер" и r е Dp введенные в А.3.3.1 функции xр (rc (р)) = g (s*(r)), где
Dp = {r е R" : rM(р) gM(р)(s*(r)X rc(р) = gc(р)(s*(r))= гА(р) gf(p)(s*(r))}.
2) Разбиения B и B0 совпадают и соответствующий g(s) прямой механизм неманипулируем. ^
Таким образом, мы получили условия на непрямой механизм, достаточные для существования эквивалентного прямого механизма (Т.3.2.1). Несмотря на то, что эти условия накладываются на исходный непрямой механизм, проверка их в общем случае затруднительна.
В следующем параграфе мы рассмотрим способы применения Т.3.2.1 для доказательства существования эквивалентного прямого механизма для частных случаев механизмов планирования.
§4. Существование эквивалентного прямого механизма для дифференцируемых процедур планирования и линейных процедур планирования
Условия А.3.3.1-3.3.3 существования эквивалентного прямого механизма, хотя и являются достаточно общими, недостаточно конструктивны и требуют упрощения. Особенно простой вид они принимают для дифференцируемых и линейных процедур планирования.
Будем говорить, что функция n - переменных g(s) дважды непрерывно дифференцируема на множестве S если в любой точке s е (0; 1)n определены и непрерывны производные функции g (s) до второго порядка включительно и если st = {0; 1} то определены и непрерывны соответственно справа и слева правые и левые производные до второго порядка включительно.
Теорема 3.4.1. Пусть функции полезности АЭ из множества I обобщенно однопиковые, процедура планирования g: S ® Rn дважды
непрерывно дифференцируема в S, для любых р ерп и ~-C(p) е[0,1]І С(р^ функции gc(р)(sc(р),~_c(р)) глобально обратимы на
(s)
dsJ
множестве sc(р) е [0,1] , матрица Якоби J(s) =
положительные диагональные миноры для всех s е S. Тогда для
имеет
механизма, определяемого S = [0, 1]п и процедурой g: S ® Rn, существует эквивалентный прямой механизм. ^
Доказательства следующих следствий 3.4.1-3.4.3 очевидны при использовании результатов о существовании обратной функции для непрерывной функции одного переменного [7], разрешимости систем линейных уравнений [1] и глобальной обратимости функций [4].
Рассмотрим дифференцируемые процедуры планирования. Отметим, что дифференцируемость в замкнутом множестве предполагает,
что окрестность точки определяется как пересечение окрестности в R n и этого множества. Дифференцируемость в открытом множестве, например
Rn , предполагает, что под окрестностью понимается, например, шар. Поэтому, при переходе от g(s), определенной на S, к G(s) - ее доопределению на все Rn, на границе S функция G не будет дифференцируемой.
Следствие 3.4.1. Пусть n = 2, процедура планирования g(s) дважды непрерывно дифференцируема и удовлетворяет следующим условиям:
lgL (s) 0, s е [0,1]2 ; dsi
Тогда для механизма определяемого S = [0, 1]2 и процедурой
g : S ® R2 существует эквивалентный прямой механизм.
Следствие 3.4.2. Пусть задана числовая матрица A размерности n х n и механизм планирования с процедурой планирования x = As + x0,
s е [0,1]n , X0 е Rn. Если все диагональные миноры матрицы A больше нуля, то для механизма определяемого S = [0, 1]n и процедурой x = As + X0, s е [0,1]n существует эквивалентный прямой механизм.
Следствие 3.4.3. Пусть процедура планирования g: S ® Rn дважды
непрерывно дифференцируема в S, и матрица Якоби J(s) =
?¦ (*)
dsj
положительно определена для всех s е S. Тогда для механизма, определяемого S = [0, 1]n и процедурой g: S ® Rn, существует эквивалентный прямой механизм.
Данный результат накладывает достаточно сильные ограничения на процедуру планирования, так как положительно определенная матрица
б й . ¦ 1 dgi dgJ
должна быть симметричной, то есть і, j е 1, - = .
ds- dsi
Отметим, что условия натуральности системы [84] в применении к механизмам планирования схожи с условиями теоремы 3.4.1.
Результаты настоящего параграфа дают удобные достаточные условия существования эквивалентных прямых механизмов планирования и значительно расширяют класс механизмов планирования, для которых доказано существование эквивалентного прямого механизма.
В следующем параграфе мы используем условия теорем 3.4.13.4.3 для анализа влияния множества возможных сообщений на существование эквивалентного прямого механизма.
§5. Влияние множества возможных сообщений на существование эквивалентного прямого механизма
Интересным представляется тот факт, что существование эквивалентного прямого механизма зависит не только от процедуры планирования, но йог множества возможных сообщений. Рассмотрим следующий пример.
Пример 5.1. Пусть механитпланирования в системе с двумя элементами выглядит следующим образом:
x2 = g2(si, S2) = Si + S2 , Si, Si 6 [0, i]2 .
Множества разбиения B приведены на рис. 3.6, а множества совокупности B0 на рис.
3.7. При этом видно, что соответствующий прямой механизм манипулируем, а множества D(c, m), D(m, c), D(a, c) не
совпадают со множествами D0c, m), D(0m, c), D(0a, c) соответственно.
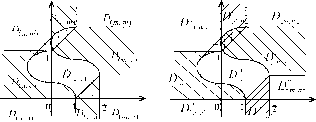
Изменяя множество возможных сообщений исходного механизма
таким образом, что новое множество сообщений будет ST = [0, i] х получим, что для нового механизма, определяемого ST и процедурой g(s), выполнены условия A.3.3.I-3.3.3, которые гарантируют выполнение теоремы 3.3.I. Тем самым, для нового механизма существует
Рассмотрим постановку следующей задачи о наибольшем множестве возможных сообщений, для которого при заданной процедуре планирования существует эквивалентный прямой механизм.
Пусть задан механизм планирования G = (S, g), g : S ® Rn, где S = П [0,1]. Функции полезности АЭ однопиковые с точками пика из
iel
Rn . Функция полезности центра Ф(x, r), где r - вектор точек пиков АЭ.
Эффективность функционирования АС K = min max Ф(g(s*), r).
reRn s*eEN (r)
Обозначим S - множество всех подмножеств S вида Пй, D, ], где
iel
0 dt D, 1. Определим подмножество S c S подмножеств вида Пй, D,], где 0 dt D, 1 таких, что для механизма G' = (S', g), где
iel
S e S существует эквивалентный прямой механизм. Решением задачи будет множество S' e S такое, что S* e Argmaxmin max Ф(g (s*), r).
S'eS reRn s*eEff(r)
Таким образом, для построения механизма, эквивалентного исходному необходимо решить задачу о наибольшем множестве возможных сообщений таком, что для построенного механизма существует эквивалентный прямой механизм. Для этого достаточно найти множества возможных сообщений такие, что выполнены условия А. 3.3.13.3.3. При этом соответствующий G = (S*, g) прямой механизм будет неманипулируемым, а множество S * максимально в смысле эффективности механизма G.
Заключение
В настоящей работе рассмотрен ряд подходов к изучению неманипулируемости механизмов управления в социально-экономических системах и определен класс активных систем (нетрансферабельными, обобщенно однопиковыми и сепарабельными функциями полезности АЭ) в которых существуют недиктаторские механизмы планирования [2,7,53].
Для активных систем с нетрансферабельными, сепарабельными и обобщенно однопиковыми функциями полезности АЭ предложен метод исследования неманипулируемости механизмов планирования, заключающийся в анализе множеств диктаторства и обобщающий методы, предложенные в работах [7,12,13,14,17,53].
На основе предложенного подхода получены условия неманипулируемости прямых механизмов планирования и условия существования эквивалентных прямых механизмов.
Приведем краткий перечень основных результатов настоящей работы и перспектив дальнейших исследований:
1. Получены достаточные условия неманипулируемости прямых механизмов планирования (Т.2.1.1);
2. Получены необходимые и достаточные условия коалиционной неманипулируемости прямых механизмов планирования (Т.2.2.1);
3. Получены достаточные условия неманипулируемости прямых механизмов планирования с векторными планами (Т.2.3.1);
4. Получены достаточные условия существования эквивалентного прямого механизма для непрямых механизмов планирования общего вида (Т.3.3.1);
5. Получены достаточные условия существования эквивалентных прямых механизмов для непрямых механизмов планирования, процедуры планирования которых дифференцируемы (Т.3.4.1) и как следствия получены условия существования эквивалентного прямого механизма для механизмов планирования частного вида:
- для механизмов с двумя АЭ, процедуры планирования которых дифференцируемы (Следствие 3.4.1);
- для механизмов, процедуры планирования которых линейны (Следствие 3.4.2);
- для дифференцируемых механизмов планирования с положительно определенной матрицей Якоби (Следствие 3.4.3).
6. Проанализировано влияние множества возможных сообщений элементов на существование эквивалентного прямого механизма.
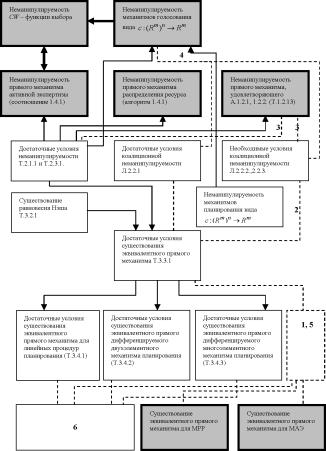
На рис. 4.1 приведена схема результатов работы (доказанные другими авторами результаты изображены жирными линиями и затенением, оригинальные результаты - тонкими линиями).
Так же на рис. 4.1 приведены перспективные задачи будущих исследований неанипулируемости механизмов планирования (изображены штриховыми линиямии, которые пронумерованы согласно следующему списку):
1. Получение достаточных условий существования
эквивалентного прямого механизма, которые гарантируют существование эквивалентного прямого механизма для механизмов распределения ресурса и активной экспертизы;
2. Изучение возможности построения эквивалентного прямого
механизма (Т.3.3.1) для случая, когда допускается
коалиционное поведение;
3. Получение необходимости в связи результатов Т.2.1.1 и Т.1.2.13;
4. Изучение манипулируемости и коалиционной
неманипулируемости для случаев, когда в качестве планов выбирается вектор Евклидова пространства;
5. Другие конструктивные достаточные условия существования эквивалентного прямого механизма;
6. Прикладные модели механизмов планирования.
7. Более общими по сравнению с исследованием неманипулируемости (в рамках общей модели, описанной в первой главе настоящей работы) являются задачи синтеза оптимальных механизмов планирования в активных системах и задачи реализуемости тех или иных соответствий группового выбора.
Литература
1 Abreu D. and Sen A. Subgame perfect Implementation: A Necessary and Sufficient Conditions. Review of Economic Theory, 1990. Vol.
50. P. 285-99.
2 Arrow K.J. Essays in the theory of risk-bearing. Amsterdam: North-Holland Publishing company, 1974. - 178 p.
3 Arrow K.J. Social choice and individual values. Chicago: Univ. of Chicago, 1951. - 204 p.
4 Arrow K.J., Radner R. Allocation of resources in large teams // Econometrica. 1979.
Vol. 47.
N 2. P.361 - 386.
5 Baryshnicov Y. Unifying impossibility theorems: a topological approach.
Adv. Applied Math, 14, 1993. P. 404-415
6 Baryshnikov Y. Topological and discrete social choice: in search of a theory. Social Choice and Welfare, 14, 1997.
P. 199-209.
7 Border K. S., JordanJ. S. Straightforward Elections, Unanimity and Phantom Voters.
Review of Economic Studies, 1983, P. 153-170.
8 Border K., Sobel J. Samurai accountant: a theory of auditing and plunder//Review of Economic Studies. 1987. Vol.54.
P.525-540.
9 Burkov V.N., Enaleev A.K. Stimulation and decision-making in the active systems theory: review of problems and new results // Mathematical Social Sciences. 1994. Vol.
27. P. 271 - 291.
10 Burkov V.N., Lerner A.Ya. Fairplay in control of active systems / Differential games and related topics. Amsterdam, London: North-Holland publishing company, 1971.
P. 325 - 344.
11 Burkov V.N., Novikov D.A., Petrakov S.N. Mechanism design in economies with private goods:trthtelling and feasible message sets.
XIII Conference on system science, 1998. Vol.3 P.255-262
12 Chichilinsky G. Fixed point theorems and social choice paradoxes. Econ.
Letters 3, 1979. P. 347-351
13 Chichilinsky G. Interesting famiilies of sets and the topology of cones in economics. Bill Am Math Society, 29(2), 1993. P. 189-207
14 Chichilinsky G., Heal G.M. The geometry of implementation: a necessary and sufficient condition for staightforwardness. Social Choice and Welfare, 14, 1997.
P. 259-294.
15 Chichilinsky G. Social diversity, arbitrage and gains from trade: a unified perspective on resource allocation. American Economics Revive, 84 (2), 1994. P. 427-434
16 Chichilinsky G. Limited arbitrage is necessary and sufficient condition for the existence of a competitive equilibrium. Economical Theory, 5(1), 1995. P. 79108
Chichilinsky G. Social Choice and the topology of space of preferences. Adv Math 37 (2), 1980. P. 165-176
Chichilnisky G. Market arbitrage, social choice and the core. Social Choice and Welfare, 14, 1997. P. 161-198
Chichilinsky G., Heal G.M. A necessary and sufficient conditions for resolution of social choice paradox. J Econ Theory, 31, 1983.
P. 68-87 Chichilinsky G., Heal G.M. Social Choice with infinite populations: construction of a rule and impossibility results.
Social Choice and Welfare, 14, 1997. P.