Решение задачи с помощью индивидуальных коэффициентов прироста
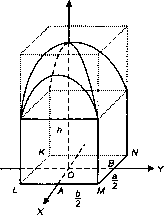
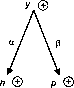
Рис. 5.1
Прямая задача: определить объем V образовавшегося тела, если стороны его основания равны а и Ь, а высота равна А. Уравнение параболоида:
х2+у2
2р
Объем образовавшегося тела:
-I}
О о
х2+у2
)dydx.
Решение задачи с помощью индивидуальных коэффициентов прироста
Необходимо увеличить объем V образовавшегося тела за счет увеличения высоты h тела и увеличения объема параллелепипеда (увеличения параметра р). Пропорции прироста регулируются коэффициентами относительной важности: для высоты h коэффициентом а - (Л(а)), а для параметрар - коэффициентом Р - (р(Р)). Целевая установка при этом выглядит следующим образом:
:А
х2+/
2/?+(р)
Введем, как и ранее, индивидуальные коэффициенты приростов:
А + ДА = kxh,
p + hp = k2p.
Если через А ?(к{) и А ?{к2) обозначить приросты объемов, которые будут получены за счет использования коэффициентов /с, и к2, то можно записать:
А?{к,) = ?{к,)-?, А?(к2) = ?(к2)-?,
где ?(к2) - приросты объемов срезанного параллелепипеда, полу
чаемого за счет применения коэффициентов кхик2 соответственно;
K(Aj), Ц2) - новые объемы срезанного параллелепипеда, получае
мого за счет использования коэффициентов к{ик2 соответственно;
V - начальный объем срезанного параллелепипеда.
В общем виде задачу обратных вычислений можно записать:
\\f{x,y)dxdy-V,
D
AF(*,) a(Pl) AV(k2) p (р2У
где p.
V
a, P
параметр функции f(x, у); искомый объем;
коэффициенты приоритетности аргументов рх и рт
Для рассматриваемой функции задача при условии применения индивидуальных коэффициентов прироста аргументов примет вид
2 2 2 , 2 _
f Ukxh-f-)dydx = V, _а _І 2Ркг
2 2
А ?{кх) а (К)
А ?{к2) Р(^)’
где у ~ новый (заданный) объем срезанного параллелепипеда;
а (А), р (р) - коэффициенты относительной важности аргументов hwp.
Найдем из первого уравнения какой-либо из искомых коэффициентов, например к? Заметим, что вследствие симметрии можно искать учетверенный интеграл на области ОАМВ:
ь
2 dx = о
J J (.klh-^j^-)dydx=4^j(kih--)dydx=4j(kihy
х2У
2рк2
2 рк2 6 рк.
ч j AM\hx
-)dx = 4(^--
о а 96 рк:
Ьх2
Ьл
ОХ
f bLha ba
1 - 4(-----
о 4 96рк2
¦) =
2 4 рк2 48рк:
=abhk,-ab^+blKv. ’ 24 рк2
\1рк2 4%рк:
ab(a2+b2)_T
L,
24 р
kxT = + V
k2
Введем обозначения:
abh = Т,
и за
пишем
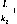
,3 ь
2р 6
г,п Л},.. Х2+У2.,, J.. , х2у /.§, J Шк Ьх2 Ь\,
V(kl)=4ll(klh-)dydx=4l(klhy---)ldx=4l -_)Л =
2 4р 48/7
О О
bk,hx Ьх3
^ = аЫікх - - = Ткх - L.
0 1 24/7 1
Ьъ х
=4(-
12/7 48/7
Отсюда прирост, зависящий от к? равен:
А V(kx) = Tk\-L-T + L = Tkx-T.
Аналогично рассчитаем объем, получаемый за счет применения к2:
dx = 4j(Ь±- Ьх1
V(k2) = 4]f(h-?f-)dydx=4f(hy
-)dx =
2 4 рк2 48рк:
2ркг
Mr Ьх3 Ьъ х
" z Прк2 ~4?рк2
2рк2 6 рк:
ab(a2+b2) 24 рк2
ab* 24 рк2
Ъа
- = abh -
2 =аЫг-~
О 24 рк2
Соответствующий прирост
д v(2) = T--T+L = L-.
2 кг к2
Теперь можно воспользоваться вторым уравнением из системы уравнений для отыскания коэффициента к2:
а_ А?(кх) Щ-Т
Р~Л?{к2) L_l_'
к2
Пример (рис. 5.1): а = 1; b = 2; h = 4;р = 1; а = 0,7; Р = 0,3, L = 0,42; Г =8.
Исходный объем равен Т- L- 8 - 0,42 = 7,58.
Допустим, желаемый объем равен 8,58, т.е. V = 8,58.
О 42 +8,58
Тогда к2 = - ’ = 4,7; *,=-= 1,08.
Проверка. abhkx ~ = Tkx = 81,08-^^ = 8,55*8,58.
4-, 1
Практический интерес представляют все целевые установки, рассмотренные в гл. 2. В первую очередь:
+ ч х2+у2 + .+ . х2+у2
? ' 2/7 (Р) ? ' 2/7_ (р)
- , х2+у2 _ х2+у2
к2
получим к2 =
так как
к, =
ОХ+РГ-РК
2/7-(р)
2/7 ((3)
Z =А (а)-; z =й (а)-
Решение задач без указания приоритетов целей
Допустим, коэффициенты относительной важности целей указать невозможно или же они несущественны. Тогда можно отыскать такой коэффициент к, который, будучи умноженный на р и h, даст искомый прирост объема.
Из предыдущего варианта решения задачи известна функция, с помощью которой можно подсчитать объем. Она имеет вид
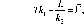
Tk2-Vk-L = 0\
V + yjv2+4TL 2Т '
Пример:а=1;Ь = 2;й = 4;р = 1; К = 8,58; V + А? = 8,58; F=7,58.
ab(a2+b2)_ l-2(l + 4) =Ш=042;
Тогда: T=abh=8; L =
24p
24-1 24
8,58 + ^73,6 + 4-8-0,42 _t
_ _ i,iz.
2-8
Проверка. ГЛ:--=8-1,12-=8,95-0,375=8,575*8,58.
^ 1,12
5.2.
Обратные вычисления на дифференциальных уравнениях первого порядка
Вначале рассмотрим прямую задачу.
Для моста строится каменный бык высотой 12 м с круговыми горизонтальными сечениями. Бык рассчитан на нагрузку р = 90 т
(помимо собственного веса). Плотность материала у = 2,5-Дг-.
. м
Допустимое давление составляет к = 300 . Найти площади вер-
м2
хнего и нижнего оснований (рис. 5.2).
Решение прямой задачи. Площадь s0, м2, верхнего
т
основания при допустимом давлении Л: = 300может выдержать
м
нагрузку ksQ, а по условию ksQ= р. Следовательно,
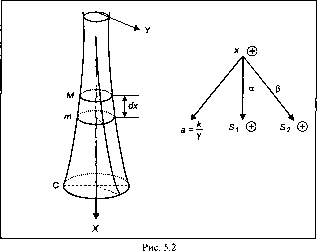
Обозначив через л; расстояние сечения s от верхнего основания, можно выделить бесконечно малый горизонтальный слой. Площадь его нижнего основания превышает площадь его верхнего основания на ds.
Поэтому у нижнего основания предельная нагрузка больше на величину ysdx. Получается дифференциальное уравнение: kds = ysdx:
Разделив переменные и интегрируя при начальных условиях
гА, у} 1 sx у
х = 0, s = sQ, можно получить J = J ах, откуда имеем In =х.
So S к о s0 к
Чтобы найти площадь нижнего основания, необходимо под-
т
ставить х = 12 при sn = 0,3; у = 2,5; к = 300. Переходя к десятич-и м
s 2 5
ным логарифмам, получим lg^ = М^^12, где М - модуль перехода от натуральных логарифмов к десятичным, М = 0,43429, откуда j, = 0,33.
Задача обратных вычислений. Известны площади нижнего s] и верхнего sQ оснований каменного быка. Обозначим через х высоту моста. Необходимо определить новые sl и $0, если высота моста изменилась на величину Ах.
Остальные данные прежние. Запишем, чему равна высота моста:
х = In .
Допустим, целевая установка, представленная графически на рис. 5.2, имеет вид
Введем индивидуальные коэффициенты приростов аргументов:
s{ + Asj =kxsl9 s0 + AsQ=k2sQ.
Это позволяет составить обычную систему уравнений:
_ а
k2s0-AsQ р’
Л 1 Мі х-\- Ах - а\п-- -.
k2s0
Решая данную систему уравнений, получим
аА:2^0-(ХУ0+Р^
P^j -оу0
((Зу-сфо ’
к 0,7 1,0278 0,3-0,7 0,3+0,3 0,33 1 " 0,30,33
Х_
а
15
120
0,125
= 1,1327;
= 0,125, у = е
1,059;
=1,0278;
0,3 0,33-0,7 0,3 (0,3 1,1327-0,7)0,3
1,059 0,33 1,0278 0,3
л: = 120 In
=14,9966*15.
В данном случае в результате решения дифференциального уравнения получена логарифмическая функция, которая и обеспечила решение задачи обычным образом.
Практический интерес представляет большинство целевых установок, рассмотренных в гл. 2. Это в первую очередь:
?).
КФ)’
У *.+ (Р)
КФ).
му
-itaiW.
У \(Р)
Изменение площадей плоских фигур
5.3.1.
Площадь фигуры, ограниченная линиями
Вычислить площадь фигуры (рис. 5.3), ограниченной линиями: у=х; у=5-х;х=\;х=2.
Запишем уравнения этих линий в общем виде: у, =с-х; у2 = рх. Допустим, что необходимо уменьшить площадь фигуры за счет увеличения параметра р на величину Ар и уменьшения параметра с на величину Ас, т.е.
у, =(с-Ас)-х=^--х', у2=(р+Ар)х = рхк2.
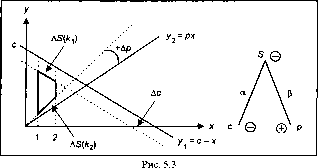
Если через AS^) и AS^) обозначить приросты площади фигуры, получаемые за счет уменьшения параметра с и увеличения параметра р, то соответственно можно записать:
А5(*,) = 5(*,)-5; AS(k2) = S(k2)-S, где S(k{) - площадь, получаемая за счет применения коэффициента
S(k2) - то же 2;
S - исходная площадь фигуры.
Зная предпочтения в уменьшении площади, приходим к следующей задаче обратных вычислений:
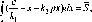
где S - желаемая площадь фигуры.
Поиск кх и убудем вести последовательно. Прежде всего выразим один коэффициент через другой:
a k\
J(" * - k2px)dx = ^-\dx-\xdx ~кгР \xdx=j- Ф" ¦a) ¦-^r\ a ~кг Pу | * =
k2P-
=f(6-a)--
Введем обозначения:
А2 Л „
о а _ с
= Z,(b-a)-Z-k2pZ = S и полу-
2 *і
чим
к -А К2 -
(b-a)-Z-S pZ '
Теперь определим, чему равны числитель и знаменатель второго уравнения рассматриваемой системы:
Г (c-x- -x)dx c\dx\dx-2\xdx
AS(*,) Г *. ’ { кх\ { I (к2рх - px)dx рк2 I xdx - р\ xdx и \ с /и Ч 2(Ь2-а2)
ф-а)- (Ь-а)----- рк.
Ь2 -а2 Ь2-а2
-Р-
Ь2 -а2
Если, как и ранее, считать, что-= Z, получим
ф-а)--(b-a)-2Z
pk2Z~pZ ф-а)
aZ + aS + apZ + fo(b-a)-2$Z
Пример:с = 5;/? = 1; я = 1; 6 = 2; а = 0,7; Р = 0,3; Z = 1,5.
2
Прямая задача: S = j(5-x-x)dx = 2.
Задача обратных вычислений: необходимо уменьшить площадь до S = 1,5. Тогда получим
кх =
= 1,33; к2 =0,51.
5-1
0,7-1,5 4-0,7-1,54-0,7-1-1,5 4-0,3-5-1-2-0,3-1,5 2
Проверка. |(--x-0,5\x)dx = ~(b-a)-Z-k2pZ = \,49\,5.
1 1,33 к^
5.3.2.
Решение задач без указания приоритетности целей
Общий вид уравнения
ъ
I (--x-k2x)dx = S.
а к\
При к. = к = к имеем
~--x-kpx) = S', (b-a)-Z-kpZ =S; к к
к -(Z + S) + yl(Z + Sf+4pZ(b-a^ t 08 2 pZ ’ '
Проверка. 5-1,08-1,5 = 1,511,5.
5.3.3.
Площадь фигуры, ограниченной кривыми
Вначале рассмотрим частный случай решения задачи обратных вычислений, где фигурирует лишь одно неизвестное. Метод обратных точечных вычислений здесь не нужен.
Пр ямая задача. Вычислить площадь фигуры, ограниченной линиямиу = 4-л:2иу = 0. Площадь фигуры, которую следует определить, изображена на рис.
5.4, где сплошная линия - указанная кривая.
2 2 2 S= J (4-x)dx= J Adx- J xdx= 4x -2 -2 -2
2 _32 3 -2 3
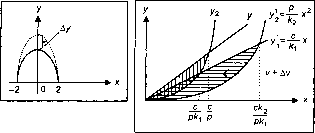
10,07.
Задача обратных вычислений. Площадь фигуры необходимо увеличит до 20 ед., т.е.
S =S + AS = 20. Тогда
S + AS = J (4 + Ау)-J xdx= J 4Jx +J Aydx-J xdx = +4Ay.
Отсюда: Ay = 2,3.
Проверка. J 6,3dx- J xdx = 19,9 20.
Если в задаче неизвестных больше одного, то необходим аппарат обратных вычислений.
Пусть площадь фигуры задана следующими уравнениями (рис. 5.5):
Это значит, что необходимо увеличить площадь фигуры за счет изменения параметров функций следующим образом:
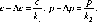
к\ к2 Рк 1
Обозначим площадь исходной фигуры через F, а желаемую
площадь - через ?+А? = ?. Тогда можно сделать следующий расчет:
Решив уравнение пятой степени относительно к{ и подставив его во второе уравнение системы, получим искомые коэффициенты прироста. Здесь так же, как и в предыдущих разделах, для решения задач можно использовать типовые целевые установки.
Обратные вычисления на логарифмических, показательных и степенных функциях
5.4.1.Логарифмические функции
Рассмотрим логарифмическую функцию, у которой изменяется само логарифмическое выражение.
1. Целевая установка: Р+ =(lg+ /7)a+(lg+ С)р.
Задачу будем решать с помощью индивидуальных коэффициентов прироста каждого из аргументов:
lgIJ+A\gIJ = kl \%П, lgC + AlgC = A2lgC.
Задача принимает вид:
P+AP=ki \gll+k2 lgC,
А, \gI7-\gIJ _ a A2lgC-lgC~p'
Решив данную систему относительно А, и к2, получим:
, _ a(P+AP)+pig/7-algC
/г _ ¦_ ,
к2 =
(P+AP)-kl\gn
lgC
Пример (рис. 5.6). /#П = /#100 = 2; lgC = 1000 = 3; Р = 5; АР = 3; а = 0,6; |3 = 0,4;
А, =1,9;к2 =1,4; 1ёЯ + Д ^Я = А, ^Я = 1,9-2 = 3,8; lgC + AlgC = A2 lgC = l,4-3 = 4,2.
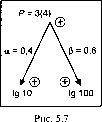
Проверка. Р+ДР = 3,8 + 4,2 = 8.
Целевые установки вида: Р+ =lg+ Я+lg С, Р+ =\g~ Я + lg* С,
Р~ =lg+ Я + lg' С и т.д. реализуются аналогично.
Проанализируем логарифмическую функцию, у которой изменяется подлогарифическое выражение.
2. Целевая установка: Р+ = Ig#+(a)+IgC+(P).
Если, как и в предыдущем варианте, использовать индивидуальные коэффициенты, то можно записать:
lg(tf+A/7) = lgfcjtf,
lg(C + AC) = lg?2C.
Тогда задача обратных вычислений принимает вид:
P+AP = \gk]n+\gk2Ci ¦ 10'8|Д-Я_а
10lgi2C _С Р’
Решая систему уравнений, получим:
lgkx=a(P+AP),lgk2C = (P+AP)-lgkln.
Система имеет решение при условии, что (3 ос.
Пример (рис. 5.7).
П = 10; С = 100; Р = 3; АР = 1; a = 0,4; Р = 0,6; lgкхП= 0,4 - 4 = 1,6; \gk2C = 4 - 1,6 = 2,4; lg(Я + Д/7) = 1,6; lg(C + ДС) = 2,4; Ю'-6= П + Д/7; Д/7 = 29,8; ІО2-4 = С + ДС; ДС = = 141,19.
Проверка. P+A/ = lg(10+29,8)+lg(100+141,19)=3,9818*4.
Здесь также можно использовать большинство целевых установок, рассмотренных ранее, а именно:
Р* =lg/7++lgC; P+=lgtf'+lgC+; Р' = lg П'+ lg С~ и т.д.
5.4.2.
Показательная функция
3. Целевая установка: р+ =(П)х+^аі +(С)-К+(Р\
Введем индивидуальные коэффициенты приростов:
Пх + П*х = Пк'х,
су+САу = СкгУ.
Составим систему уравнений:
Р+АР=Пк'х +Ск'у, 4 Пк'х-Пх а
скгУ Су э‘
Решая ее, получим:
пк'х =(Р+АР)-СкгУ, СкіУ =аСу + $(Р+АР)~рях.
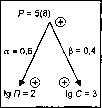
Пример (рис. 5.8). Я = 33= 27; С = 24 = 16; Р = 43; АР = 7; а = 0,6; Р = 0,4; С**' = 18,8; Пк'х = 31,2; ГР + ЯЛ' = 31,2; Я*1 = 4,2;
Ах = ^^ = 1,29; С + СЛ = 18,8;СЛі'=2,8;Ау=^^ = 1,49.
In 3 ' In 2
Проверка. Р+АР = З3 + 3129 + 24 + 21'49 = 49,93 *50.
Степенная функция
4. Целевая установка: Р+ =(П+(а))а +(С)+(Р))*.
Как обычно, введем индивидуальные коэффициенты:
(П+АП)а=к1Па]
(С+АС)Ь =к2Сь.
Определим коэффициенты прироста стандартным образом:
, а(Р+АР)+ріТа -аСь
1 па ;
, {Р+АР)-кхПа
Ч- ~ь -
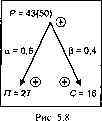
Пример (рис. 5.9). /7" = 52 = 25; С6 = З4 = 81; Р = 106; ДР= 14; а = 0,6; (3 = 0,4; к, =1,336; к2 =1,069; (77+Л/7)2 = 1,336-52 =33,4; (С+ДС)4 =1,069-34 =86,589; П+АП=^ЪЪА\ ДЯ=5,575-5 = 0,779; С+АС=$І$6,589; ДС=3,05-3=0,05.
Проверка. Р+ДР=(5+0,779)2 +(3+0,05)4 =120,004*120.
5. Целевая установка: Р+ =(#+(а))в +(С)_(Р))*.
Как и ранее, введем индивидуальные коэффициенты:
(П+АІТ)а =кхПа,
Сь
(С-АС)а --J--
Составив стандартную систему уравнений и решив ее, получим:
-а(Р+АР)+рЯа +аСь _
1~ І7аф-а) ’ (Р+АР)-кхПа
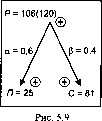
Пример. Па -1} - 8; Сь = З4 = 81; Р = 89; АР = 11; а = 0,6; Р = 0,4; кх = 5,125; к2 = 1,373; (Я + Д/7)3 = 5,125 - 8 = 41;
(С-АС)4 =-^ = 58,99; Р+ДР=41+58,99=99,99*100;
1,373
77 + Д/7 = ?4І = 3,448; С-ЛС = ^/58,99 =2,77; А/7 = 3,448-2=1,448; ДС=3-2,77 = 0,33.
Проверка: Р+АР=(2+1,448)3 + (3 - 0, ЗЗ)4 = 99,86 * 100.
Глава 6ИНСТРУМЕНТАЛЬНЫЕ СРЕДСТВА, ПОДДЕРЖИВАЮЩИЕ ФОРМИРОВАНИЕ РЕШЕНИЙ НА ОСНОВЕ ОБРАТНЫХ ВЫЧИСЛЕНИЙ
Практическое применение обратных точечных вычислений в формировании решений требует учета следующих обстоятельств:
- изменение значений терминальных вершин деревьев целей, вероятностей и вывода не может быть безграничным, ибо ресурсы предприятия всегда лимитированы;
- формирование решений должно базироваться на оценке альтернатив и выборе среди них наилучшего в отношении принятых на конкретном предприятии критериев;
- инструментальные средства, ориентированные на выполнение обратных вычислений, должны функционировать в форме программной оболочки, не требующей программирования и обеспечивающей оперативное изменение целей лица, формирующего решение.
С учетом перечисленных обстоятельств рассмотрим, каким образом должны быть реализованы инструментальные средства, предназначенные для формирования решений с помощью обратных точечных вычислений.
Учет ограничений в процессе формирования решений
Предприятие или организация для достижения главной цели своего функционирования обладает ресурсами, которые всегда ограничены. Существуют следующие виды ресурсов: материальные, финансовые, трудовые, энергетические, информационные, временные и др.
Распространенные в настоящее время системы формирования решений, известные как системы поддержки принятия решений, ориентированы на прямые расчеты. Это является причиной того, что в процессе вычислений требуется одновременный учет ограничений на все ресурсы. Отсутствие в надлежащем объеме даже одного из них делает решение задачи невозможным.
Например, если в задаче исследования операций, где в качестве ограничений используется система неравенств (равенств), хотя бы один из ресурсов не удовлетворяет указанному ограничению, то задача не имеет решения.
Кроме того, большинство методов, базирующихся на прямых вычислениях, предлагают жесткие решения, что ведет к неустойчивому функционированию систем любого характера. Это является одной из главных причин перехода к мягким вычислениям, более толерантным к окружающей среде, которые приближают принятые решения к реальным ситуациям.
Именно такие характеристики можно заложить в системы, базирующиеся на обратных точечных вычислениях.
В контексте мягких вычислений понятие ресурс следует рассматривать расширительно: это значит, что в качестве ресурса рассматриваются и объем финансов, за счет которого может расширяться производство, и предел снижения продажных цен на продукцию, выпускаемую предприятием, и предел роста кредитов, который может позволить себе предприятие, и т.д.
Замечательное свойство мягких обратных точечных вычислений заключается в том, что при истощении одних ресурсов возможно достижение главной цели за счет других. За пояснениями обратимся к рис.
6.1.
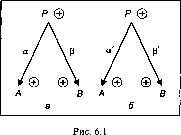
Как правило, перерасчет показателей происходит либо в пределах заранее указанных ресурсов, либо в режиме изменяемости ресурсов, задаваемых пользователем в процессе решения задачи. Если перерасчет происходит в пределах указанных ресурсов, т.е. существует некоторый предел прироста показателей, то при достижении такого предела должно произойти динамическое перераспределение КОВ. С помощью рис.
6.1, а рассмотрим этот процесс.
Допустим, значение узла А превысило допустимый предел, т.е.
Л + АЛЛ + АЛД0П.
Тогда для узла А рассчитывается а', гарантирующее АЛ = ДЛдоп,
а (У приобретает новое значение, обеспечивающее достижение требуемого АР (рис. 6.1, б). Формула для перерасчета следующая:
а, = аг*А[
где а' - новый КОВ, обеспечивающий достижение А/4Д0П;
АА[ - допустимый предел изменения ААІ;
ААІ - прирост, требуемый коэффициентом а.
Для расчета (У прежде всего следует определить новый вес оставшихся показателей:
п '
где ^ а,' - сумма всех вновь рассчитанных КОВ; пХ - число вновь рассчитанных показателей.
Тогда КОВ для каждого вновь рассчитанного показателя равен:
Р
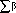
где т - число показателей, не изменивших свой статус;
Ру - вновь рассчитанный КОВ для показателя;
Ру - предыдущее значение КОВ для показателя;
т
j -сумма всех КОВ, не изменивших свой статус.
Таким образом, в случае надобности перерасчет происходит для тех вершин дерева, которым указанного ресурса не хватает. Заимствование ресурса происходит у соседа справа, т.е. используется ресурс, предназначенный для прироста вершины, находящейся справа от текущей. Если и этого не хватило, то происходит обращение к следующей вершине, находящейся справа, и так до конца дерева целей.
Не исключено, что для достижения главной цели ресурсов на предприятии не достаточно, о чем должна оповещать в конце концов система формирования решений.
Принцип обращения за ресурсами к соседу справа восходит к основам логического программирования, и, как известно, ориентирует на обработку знаний в последовательности сверху-вниз-слева-направо. Применение этого принципа для построения систем формирования решений на основе обратных точечных вычислений снимает множество проблем как теоретического, так и практического характера.
Формирование альтернатив, их оценка и выбор
Добиться главной цели, представленной с помощью дерева, можно путями, число которых трудно подсчитать. Пока не существует какого-либо метода, который позволяет осуществлять поиск альтернативы, последовательно отбрасывая ненужные, как это делается в математическом программировании.
Сегодня можно получить результат, лишь определив разумное множество альтернатив, среди которых на основании некоторого критерия выбирается один.
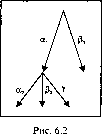
Получить множество альтернатив, отражающих результаты обратных вычислений, можно путем табулирования коэффициентов относительной важности целей в указанных заранее границах. Иллюстрацией результатов этого процесса служит рис. 6.2, где представлен фрагмент дерева целей, у которого КОВ изменяется в следующих границах:
0,6аі 0,8; 0,2pj0,4; 0,3а2 0,6; 0,1Р2 0,3; 0,2у 0,1.
Как правило, лицо, формирующее решение, может также изменять и граничные значения ресурсов, пытаясь получить вариант решения, наиболее выгодный в настоящее время. Например, если есть возможность изменять ограничение на ресурс а на величину от А до А , а ресурс b - от В до В, то, естественно, число альтернатив еще больше возрастет.
Некоторые варианты достижения главной цели, которые могут быть получены с помощью представленного на рис. 6.2 фрагмента дерева целей, показаны в табл. 6.1.
Шаг табуляции для КОВ равен 0,1, для ресурса а - 10 ед., для ресурса b - 0,01 ед.
| Таблица 6.1 Варианты значений коэффициентов относительной важности целей |
|||||||||||||||||||||||||||||||||
|
1. Лучшим будет тот вариант решения, который обеспечивает максимальное продвижение к цели с минимальным заимствованием ресурсов у соседа справа.
2. Лучшим будет тот вариант, который обеспечивает максимальное продвижение к цели с минимальным заимствованием у любого партнера (дешевый кредит).
Первый критерий предполагает жестко установленную последовательность заимствований, соответствующую расположению терминальных вершин дерева целей. Второй критерий такой последовательности не предполагает. Заем будет сделан в той терминальной вершине, где платить за него придется меньше всего.
Критерий дешевого кредита более точный, так как позволяет управлять заимствованием, исходя не из наперед жестко заданной схемы (слева направо), а на основе схемы, учитывающей предпочтения не только у соседа справа, но у всей совокупности терминальных вершин.
Совершенствование предложенных здесь критериев выбора лучшего решения может быть продолжено в направлении установления некоторой границы, заимствование в пределах которой может не штрафоваться или штрафоваться по линейной зависимости, а за ее пределами - более жестко, например, согласно экспоненциальной зависимости. В арсенале разработчика системы здесь может использоваться весь перечень известных ему функций. Более подробно об этом можно прочесть в [5].
Разработка систем формирования решений на основе программных оболочек
Систему формирования решений, ориентированную на использование результатов обратных вычислений, целесообразно создавать на основе программных оболочек. Характерная черта такого рода инструментальных средств заключается в том, что они позволяют без программирования изменять как процесс расчета, так и форму представления знаний.
Для обратных вычислений требуются следующие формы представления знаний: дерево целей, дерево вероятностей, дерево вывода и нечеткие множества. Обработка деревьев целей и вывода возможна по принципу сверху-вниз-слева-направо, а дерева вероятностей - сверху-вниз. Состав системы формирования решений, ориентированной на применение результатов обратных вычислений, представлен на рис.
6.3.
Главными компонентами системы являются база данных и база знаний.
База данных используется в качестве внешнего их источника и содержит информацию о состоянии дел как на самом предприятии, так и за его пределами.