Поиск вероятности появления события в серии испытаний
Р(А X В) - вероятность того, что случайная величина л; примет значение на отрезке (А, В);
±Ах\, ±Ах2 - приросты (положительные или отрицательные) границ отрезка (А, В), которые обеспечивают требуемый прирост вероятности попадания случайной величины л; в отрезок;
ос, Р - приоритетность направлений при расширении границ
попадания случайной величины.
Пример. Допустим, известна функция распределения, имеющая вид:
F(x) = -{x-\f ,\хЪ.
4
Вначале решим задачу следующего содержания: определить вероятность того, что случайная величина х в результате опыта примет значение на отрезке (1; 2). Исходя из свойств функции распределения, имеем:
Р(1 х 2) = F(2)-F(l) = 0,25.
Теперь сформулируем задачу обратных вычислений: на сколько следует расширить границы попадания, чтобы вероятность выросла до 0,3. При этом приоритеты расширения границ следующие: для нижней границы - 0,4, для верхней - 0,6. Теперь система уравнений примет вид:
0,3 = -((х2 +Лх2)-1)2 -((*] +Дх,)-1)2,
4 4
Ах2 0,6 Ах{ 0,4
Решив систему уравнений, получим:
Axj = 0,0425; Ах2 =0,1.
Отсюда границы участка [1; 2] изменятся и будут следующими: [1,0425; 2,1].
Проверка. - (2,1 -1)2 -- (1,0425 -1)2 0,3.
4 4
Здесь так же, как и ранее, следует внимательно проанализировать исходные данные, от которых зависит результат решения. Аналогично решаются задачи, в которых задана плотность распределения.
Поиск вероятности появления события в серии испытаний (формула Бернулли)
В управлении рисками достаточно часто применяется формула Бернулли для определения вероятности Р(п, т) того, что в результате проведения п независимых испытаний некоторое событие А наступит ровно т раз. При этом в каждом из таких испытаний данное событие наступает с определенной вероятностью Р(А).
Сформулируем задачу обратных вычислений следующим образом:
известна вероятность того, что в результате проведения п независимых испытаний событие А наступит т раз (Р(п, т)). На сколько следует увеличить число независимых испытаний (Aw) и постоянную вероятность АР(А), для того чтобы вероятность наступления события А увеличилась на АР(п, т).
Если, как и ранее, использовать метод обратных вычислений без коэффициентов прироста, то для решения этой задачи надлежит записать следующую систему уравнений:
Р(п,т) + АР(п, т) = (Р+ДР)т (1 - P)n+tm~m,
т\(п + Ап-т)
’ АР _ а(Р)
Ап Р(л) ’
где а(Р) - коэффициент приоритетности наступления события, характеризуемого вероятностью Р(А);
Р(/?) -коэффициент приоритетности увеличения числа независимых испытаний п.
Заканчивая изложение теоретических основ обратных вероятностных вычислений, еще раз обратим внимание на необходимость внимательного анализа исходных данных, так как легко получить бессмысленные результаты, если у лица, принимающего решение, слишком высокие требования.
Глава 4ОБРАТНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Экспертные системы, как яркое и когда-то быстро прогрессировавшее направление в одной из областей искусственного интеллекта, в последнее время перестали привлекать внимание как теоретиков, так и практиков. Теоретики охладели потому, что, за исключением некоторых ответвлений, данное направление исчерпало себя и перешло в ранг технологии, превратившись в одно из средств информационного обслуживания. Практики же в определенной своей части разочарованы тем, что функционирующие экспертные системы, односложно отвечая на вопрос: Что делать?, не в состоянии подсказать пользователю: Как делать?. На вопросы вида: Будет ли наблюдаться деловая активность? или Покупать ли акции на землю? системы, как правило, выдают ответ в форме ДА или НЕТ, с числовой оценкой его достоверности (в форме коэффициента определенности).
При этом они не способны ответить на вопрос: Что необходимо предпринять для того, чтобы деловая активность возросла? или Что необходимо предпринять, чтобы цены на акции поднялись (опустились) на заданную величину?.
Лицо, формирующее решение (ЛФР), хочет указывать приемлемый для него уровень достоверности получаемого ответа и знать обстоятельства, при которых этот уровень возможен. Например, после получения положительного или отрицательного ответа на один из указанных вопросов с коэффициентом определенности, равным 0,24, у ЛФР возникает желание узнать, что следует предпринять для того, чтобы рост деловой активности повысился, причем коэффициент определенности такого роста был не менее 0,7.
То же самое можно потребовать от системы и относительно акций.
Получить подобные результаты можно, если снабдить экспертную систему средствами обратных вычислений. Прежде чем перейти к их детальному изложению, необходимо остановиться на теоретическом базисе, положенном в основу обработки нечеткой информации.
Одно из главных достижений в области экспертных систем, которое рассматривалось как серьезный шаг в развитии инженерии знаний, заключалось в возможности использования мягких вычислений для обработки неточной и неполной информации. Термин мягкие вычисления введен Л. Заде [9].
Главным принципом мягких вычислений является терпимость к неточности информации для достижения приемлемых результатов. Часто это единственно возможный путь к достижению целей принятия решения. В отличие от жестких вычислений, базирующихся на детерминированных или точных моделях и использующих классическую математическую логику и точные методы, мягкие вычисления более близки к реальной информации, поступающей из окружающей среды.
И эта информация редко бывает точной, большей частью она приблизительна, отрывочна, противоречива.
К настоящему времени мягкие вычисления развились в комплексную дисциплину, которая включает:
- нечеткую логику и теорию нечетких множеств;
- системы приближенных рассуждений;
- системы управления приближенными данными (нейросети и генетические алгоритмы);
- теорию хаоса;
- фрактальный анализ.
Далее будут рассматриваться лишь два из перечисленных направлений мягких вычислений, а именно: системы приближенных рассуждений и нечеткие множества. В таких системах может использоваться один из двух механизмов оперирования с неточными высказываниями (суждениями):
- присоединение - процесс вывода результатов рассуждений выполняется аналогично точным выводам, но параллельно этим выводам происходит специальный пересчет, позволяющий выявить уровень приблизительности полученных результатов;
- вывод осуществляется на специально разработанном языке представления неточностей.
Рамки применимости классической математической логики и теории вероятностей к моделированию реальных процессов определяются четкостью, измеримостью и достоверностью исходной информации. К сожалению, большинство перечисленных свойств не характерны для используемых человеком знаний. Как правило, это приближенные рассуждения, сочетающие в себе многочисленные динамически изменяющиеся шкалы. Это означает, что если теоретико-вероятностные модели в соответствии с указанными ограничениями должны ориентироваться на единую шкалу измерения объектов, процессов, состояний, то реальные модели, отражаемые с помощью приближенных рассуждений (знаний), базируются на многих шкалах.
Такие шкалы, подобно тому, как это делает человек, должны выбираться динамично, отражая природу измеряемого процесса в соответствии с целями моделирования и с реальной ситуацией. Отсюда вполне естественным выглядит применение классической математической логики и теории вероятностей лишь в качестве теоретической основы, используемой для построения методов, более адекватно отражающих реальные процессы.
Рассмотрим, каким образом можно воспользоваться механизмом присоединения, базируясь на фундаментальных конструкциях математической логики и основополагающих идеях теории вероятностей. Для этого следует выделить такие понятия как импликация (ЕСЛИ - ТО), конъюнкция, дизъюнкция, условная и безусловная вероятность.
Дерево вывода
Достаточно сложно создать цепочку рассуждений с несколькими вероятностными условиями, связанными логическими операциями И, ИЛИ, НЕ. Поэтому, создавая многие экспертные системы, разработчики отказываются от условных вероятностей и вместо них используют приближенные вычисления.
Понятие вероятности заменяется на коэффициент определенности.
Существует достаточно методов, ориентированных на учет неопределенности процессов, событий, объектов и т.д. Далее пойдет речь об одном из них, способном отражать неопределенность с помощью нечетких множеств и деревьев вывода. Последние, как известно, синтезируют множество правил, записанных в форме ЕСЛИ-TO.
Каждое правило характеризуется рядом параметров, обозначаемых специальным образом.
Пусть известно правило:
если а, то Ь.
Оно характеризуется следующими параметрами:
а - условие (посылка);
b - заключение (результаты вывода);
ct(a) - коэффициент определенности условия;
с/(пр) - коэффициент определенности правила (импликации);
ct(b) - коэффициент определенности заключения.
Все правила могут быть обратимы (о) или необратимы (н). Коэффициенты определенности могут изменяться в диапазоне от -1 до 1. Единица присваивается в том случае, если условие, правило или вывод заслуживают полного доверия, и минус единица, если они не заслуживают никакого доверия.
Более подробно об этом можно прочитать в [4].
Так как число формул, с помощью которых обрабатываются правила вывода, невелико, прежде чем приступить к рассмотрению обратных вычислений, приведем их с краткими пояснениями и примерами.
Существует несколько типов правил, на основе которых вычисляются коэффициенты достоверности заключения:
т и п 1 - правило содержит одно условие;
т и п 2 - правило содержит несколько условий, связанных союзом И;
т и п 3 - правило содержит несколько условий, связанных союзом ИЛИ;
т и п 4 - одно заключение поддерживается несколькими правилами.
На рис. 4.1 типы правил представлены графически.
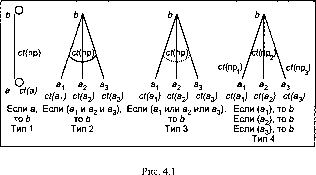
Содержание приведенных правил может быть, например, таким:
тип 1 - если ВВП возрастет, то реальная заработная плата возрастет;
т и п 2 - если сократится отток капитала и фискальная политика будет умеренной, то будет наблюдаться инвестиционный рост;
т и п 3 - если экспорт превысит импорт или снизится темп инфляции, то ВВП возрастет;
тип 4 - а) если себестоимость продукции уменьшится, то конкурентоспособность возрастет;
б) если качество продукции повысится, то конкурентоспособность возрастет.
Для каждого типа правил разработаны формулы, согласно которым происходит вычисление коэфициента определенности заключения.
Для типа 1 - если а, то Ь.
ct(b) = ct(a)-ct(np).
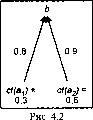
Пример: ct(a) = 0,6; ct(np) = 0,8; ct{b) = 0,6 - 0,8 = 0,48.
Для типа 2 - если (ах и а2 и... и ат), то 6.
ct{b) = ctm.n(а)- ct(np% где rtmin(а) = min (ct(ax\ct{a2\...,ct(am)).
Пример: ct(ax) = 0,2; ct(a2) = 0,8; ct(a3) = 0,5; ct(np) = 0,6; ctmin(a) = 0,2; ct(b) = 0,2 - 0,6 = 0,12.
Для типа 3 - если (я, или а2 или.. .или яш), то Ь.
ct(b) = ctmax(a)-ct(np)9 где ctmax(я) = max (ct(ax)9 ct(a2)9...9ct(am)).
Пример: ct(ax) = 0,1; ct(a2) = 0,6; ct(a3) = 0,4; ct(np) = 0,4; C/max(a) = 0?6; Ct(ty = 0’6 * ’4 = 0’24‘
Для типа 4:
вариант 1 - знаки коэффициентов определенности положительные,
ct(b) = ct(bx) + ct(b2) - ct(bx)ct(b2),
где ct(bx) =
ct(b2) = ct(a2)ct(np2).
вариант 2 - знаки коэффициентов определенности различные,
ct(b) =
ct(bl)+ct(b2)
1 - min (abs (ct(bx)), abs (ct{b2))) ’ где ct(bj), ci(b2) - те же, что и в варианте 1.
Пример (рис. 4.3): с/(я,) = 0,9; с?(а2) = -0,3; ct{np\) = 0,9; ct(np2) = 0,7; ct(b) = 0,9 - 0,9 = 0,81; ct(b2) = (-0,3) - 0,7 = -0,21;
МЬК-0,21)^
1-0,21
вариант 3 - оба знака отрицательные,
ct(b) = ct(b,) + ct(b2) + ct{b^)ct(b^),
где ct(bj), ct(bj - те же, что и в варианте 1.
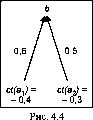
Пример (рис. 4.4): ct(a{) = -0,4; ct(a2) = -0,3; ct{np\) = 0,6; ct(np2) = 0,5; ct(bx) = -0,4 - 0,6 = -0,24; ct(b2) = -0,3 - 0,5 = -0,15; ct(b) = -0,24 + (-0,15) + (-0,24) - (-0,15) = -0,35.
Если заключение поддерживается тремя правилами с положительными коэффициентами, то формула расчета будет следующей:
ct(b) = ct(bj) + ct(b2) + ct(b3) - ct(b^ct(b^ - ct{b\)ct(b^ - c^b^ctib^ +
+ ct(b^)ct(b^ct(b^.
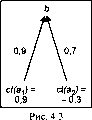
Иногда в правиле условие отрицается, например, если (не а), то Ь.
В этом случае можно поступить следующим образом: ct(ne_a) = -ct(a).
Комплексный пример прямых расчетов на дереве вывода
Представим дерево вывода, пока без содержательного наполнения условий, правил и заключений. На рис. 4.5 с помощью цифр, указанных рядом с вершиной дерева, указаны коэффициенты определенности либо условия, либо правила, либо заключения. Правило, имеющее несколько условий, связанных союзом И, представляется с помощью сплошной дуги, а союзом ИЛИ - пунктирной.
Перечеркнутая дуга свидетельствует об отрицании условия. Кроме того, в скобках указано либо о, либо н, что означает обратимость или необратимость правила.
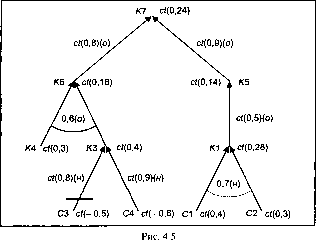
Так как выполняются прямые расчеты, вычисления ведут снизу вверх. Расчет начнем с заключения /П, выводимого на основании правила, в котором условия С1 и С2 связаны союзом ИЛИ.
Для расчета среди условий следует выбрать максимальное значение коэффициента определенности и умножить его на коэффициент определенности правила. Тогда коэффициент определенности заключения К\ равен:
ct(Kl) - max (ct(Cl), ct(C2)) - ct(np) = 0,4 - 0,7 = 0,28.
Коэффициент определенности для К5 равен:
ct(KS) = ct(K\) - ct(np) = 0,28 - 0,5 = 0,14.
Заключение КЗ выводится на основании двух правил, одно из которых обратимо, а второе нет. Правило является обратимым, если оно сохраняет смысл при отрицании условия или заключения.
Так как оба правила необратимы, необходимо проверить знак у коэффициентов определенности условий. Если этот знак отрицательный, то правило отбрасывается.
Но если при отрицательном знаке коэффициент определенности имеет еще и знак отрицания, то знак при коэффициенте меняется на противоположный. Таким образом, при рассмотрении любого правила следует проанализировать:
- тип правила (обратимо, необратимо);
- знак коэффициента определенности условия (положительный, отрицательный);
- наличие отрицания у условия.
Формально это можно представить в виде индикаторной функции:
Я = (т,з,о),
где т - тип правила;
з - знак коэффициента определенности условия;
о - знак определенности(или неопределенности).
Индикаторная функция X в полной мере используется лишь при наличии необратимого правила, отрицательного знака и наличия знака отрицания в условии. Варианты значений индикаторной функции представлены в табл.
4.1.
| Таблица 4.1 Значения индикаторной функции для необратимых правил |
||||||||||||||||
|
ct(K3) = 0,5 - 0,8 = 0,4.
Заключение Кб выводится на основании одного правила, условия которого связаны союзом И. Поэтому получим
ct(K6) = 0,3 - 0,6 = 0,18.
Заключение К7 выводится на основании двух правил. Поэтому вначале следует вычислить коэффициенты определенности, получаемые каждым из них в отдельности, а затем общий коэффициент для К1:
*(*7,) = 0,18-0,8 = 0,14; ct(Kl2) = 0,14-0,9 = 0,12; ct(K7) = 0,14 + 0,12 - 0,14 - 0,12 = 0,24.
Очень часто терминальные (нижние) вершины дерева вывода зависят от значений показателей, находящихся в базе данных. Связываются эти вершины с соответствующими показателями из базы данных с помощью реляционных выражений (больше, меньше, равно и т.д.). Элементы реляционных выражений, как правило, рассчитываются с помощью формул, иногда достаточно сложных.
В известных работах [3,4] реляционные выражения используются лишь в качестве индикаторов, которые работают следующим образом: если реляционное выражение истинно, то знак коэффициента определенности условия не меняется, в ином случае знак меняется на обратный. Иными словами, система работает в режиме булевой алгебры, что достаточно грубо отражает связь между реальными событиями. На рис. 4.6 иллюстрируется индикатор А,, принимающий значение либо 1, либо -1 в зависимости от истинности или ложности реляционного выражения.
Согласно такому подходу на рис. 4.6 коэффициент определенности равен 0,5, так как Р к. Наполним данный пример экономическим смыслом. Пусть заключение b касается покупки дома.
Используется следующее правило: если цена дома Р меньше арендной платы К, то дом покупать Ь. Коэффициент достоверности этого заключения равен:
ct(b) = ct(a) - ct(np) X,
Реляционное выражение Р к влияет на знак индикатора X, который может принимать два значения: 1 или -1. Можно получить два решения:
ct(bx) = 0,5 - 0,2 - 1 = 0,5 - 0,2 - 1 = 0,1; ct(b2) = 0,5 - 0,2 - 1 = 0,5 - 0,2 - (-1) = -0,1.
Между заключениями ct(bj) и ct(b2) существует множество значений, которые способны указать более точное отношение покупателя к сложившейся ситуации с ценой дома и его арендой. У покупателя отношение к результатам оценки зависит от того, насколько превышает или не превышает цена арендную плату (например, арендная плата превышает цену дома в несколько раз или на несколько процентов).
Индикатор X не улавливает также и подозрения покупателя, которые могут возникнуть при неумеренно низкой (высокой) цене дома или арендной платы. Иными словами, индикатор X не отражает доверие к условию, которое можно выразить с помощью нечетких множеств.
Нечеткое множество можно задать как аналитически, так и графически [6]. Для задания его аналитически воспользуемся функцией принадлежности:
г Ммі). Ммг). Мм)
Г , ) - - -
и\ и2 ип
где IV(и, ) - значение функции в точке и.;
и. - значение показателя и..
і і
Для задания отношения лица, формирующего решение, к превышению цены дома над арендной платой представим аналитически нечеткое множество следующим образом:
2,Г
0,05 0,1 0,4 0,8 0,9 1. 0,9 ’ 1,1 ’ 1,3 ’ 1,5 ’ 1,7 ’ 2’
А (превышение) =
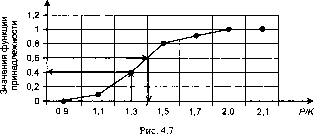
Графически функция принадлежности представится так, как это показано на рис. 4.7.
Коэффициент определенности на основе функции принадлежности можно вычислить следующим образом:
[\іа{х), если реляционное выражение истинно, ct(b) =
[г-рДх), в противном случае.
Константа г позволяет правильно учесть достоверность условия в отрицательном диапазоне. Как правило, она находится в диапазоне от 1 до 10.
Пусть в некоторый момент времени значения показателей в
Р
базе данных равны: Р = 7; К = 5. Соотношение - = 1,3 указывает
К
на значение функции принадлежности, равное 0,4. Если данное соотношение увеличится, т.е. Р будет значительно больше К, то доверие к условию правила возрастает.
Совсем другая ситуация возникает, если семантика соотно-
Р
шения -- требует колоколообразной функции принадлежности, К
представленной на рис. 4.8.
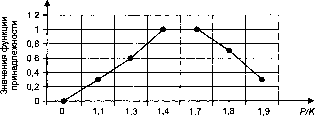
При таком понимании отношения больше при = 1,8 доК
верие к условию правила снижается, а при = 1,93 равно 0,3.
К
Обратные вычисления на дереве вывода
Теперь, когда приведены все необходимые формулы, отражающие прямые расчеты на дереве вывода, можно перейти к рассмотрению задач обратных вычислений, которые позволяют ответить на вопрос: Что следует предпринять, чтобы коэффициент достоверности какого-либо вывода повысился (понизился) на А единиц? Если в процессе прямых вычислений информация из базы данных передается в дерево вывода, то при обратных вычислениях происходит передача информации из дерева вывода в базу данных. Далее производят вычисления на основе детерминированных зависимостей подобно тому, как это было показано в гл. 2. Схемы передачи информации при прямых и обратных связях показана на рис.
4.9 и 4.10.
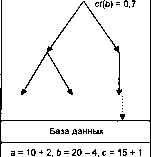
Сформулируем задачу обратных вычислений на дереве вывода следующим образом:
известны
а) дерево вывода главного заключения (гипотезы);
б) коэффициент определенности гипотезы, увеличенный (уменьшенный) до требуемой величины ct(b)±Act{b)\
в) реляционные выражения, функции принадлежности, формулы расчетов и база данных;
необходимо определить коэффициенты терминальных вершин, обеспечивающие требуемый уровень достоверности главного заключения.
Принципиальным отличием обратных вычислений от прямых является то, что при прямых вычислениях коэффициент 0,24 (см. рис. 4.9) получают исходя из значений показателей, находящихся в базе данных: а = 10, b = 20, с = 15, при обратных значения а = 10 + 2, b - 20-4, с = 15 + 1 получают исходя из задаваемого пользователем желаемого коэффициента 0,7 (см. рис.
4.10).
В рамках рассматриваемого подхода повышение достоверности правил не представляется возможным. Объясняется это тем, что всякое правило является аналогом функции, зависящей от аргументов. Правило, как и функция, устанавливает связь между исходными данными (условиями, посылками) и заключением.
Если же правило не устраивает ЛФР (низкий уровень достоверности), то так же, как и в случае наличия какой-либо функции, например детерминированной, его следует заменить. Модификация правила требует модификации дерева вывода.
Рассматриваемые далее целевые установки не столь разнообразны, как в детерминированных зависимостях, так как типов правил вывода всего четыре. Далее будем пользоваться той же типизацией правил, что и в разд.
4.1.
Обратные вычисления для правил типа 1
1. Целевая установка: ct(b)+ = ct+(a)ct(np).
Задача запишется следующим образом:
ct(b) + A ct(b) = (ct(a) + Act(a)) - ct(np).
Так как есть лишь одна неизвестная величина, прирост коэффициента определенности условия равен:
/ ч а / ч ct(b)+Act(b) ct(a) + Act(a) =-,
что графически можно представить так, как это показано на рис. 4.11.
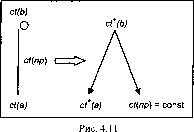
Пример (рис. 4.11). Если К\, то К5, ct(Kl) = 0,4; ct(np) = 0,8,
где К\ - означает, что возрастет индекс товарности;
К5 - возрастет внешнеторговый оборот.
ct(K5) = 0,4 - 0,8 = 0,32.
Задача обратных вычислений: пусть необходимо повысить
ct(K5) до 0,9. Получим: т(/П) + Дсг(/П)= = 1,125, что больше 1.
0,8
Очевидно, такой прирост невозможен, поэтому уменьшим его до
0,5. Тогда получим: с/(іП)+Дл(7П) = = 0,62.
0,8
Проверка. с/(^5) + Ас/(/С5) = 0,62 - 0,8 = 0,449 0,5.
2. Целевая установка: ct(b) =ct (a) ct(np). Задача запишется следующим образом:
ct(a-Act(a)~-
ct(b) - Act{b) = (ct(a) - Act{a)) - ct(np), ct(b)-Act(b)
ct(np)
Пр и м е р. Если А, то В, с((А) = 0,7; ct(np) = 0,8;
ct(B) = 0,7 - 0,8 = 0,56.
Задача обратных вычислений: требуется снизить коэффициент достоверности Act(B) на 0,3.
Получим ct(A)-Act(A) = ^^- = 0,33.
0,8
Проверка. ct(B) - Act(B) = 0,33 - 0,8 = 0,264 0,3.
Обратные вычисления для правил типа 2 3. Целевая установка: ct(b)+ =ct*in(a)ct(np),
где „ = min (ct(ai) ct(a2),..., ct(am)).
Задача запишется следующим образом:
... . . ct(b) + Act(b)
ct - (а) + Дет - (а) = -------.
mmV ) m n' ' ct(np)
Коэффициенты определенности оставшихся условий изме-
няются пропорционально коэффициенту, равному
ct- (а) + Act - (а)
min ' ' mm v 7
С'тіг
Пример (рис. 4.12). Если (АЗ и А4), то Кб, ct{Ki) = 0,4; с/(А4) = = 0,3; ct(np) = 0,6,
где АЗ - означает, что стабилизируются процентные ставки;