МЕТОД НЕЧЕТКОГО КРИТИЧЕСКОГО ПУТИ
Повышение или поддержание квалификации агента (в последнем случае стимулирование со стороны ФР может рассматриваться как тарифный оклад не зависящий от деятельности агента) требует от ФР затрат c(r). Кроме того, в целевые функции участников рассматриваемой АС могут входить константы, отражающие постоянные и не зависящие от их действий доходы или расходы (постоянные издержки, фиксированная составляющая оплаты и т.д.).
Предположим, что стимулирование агента со стороны РП и ФР известно ему на момент принятия решений о выбираемых типе и действии. В силу гипотезы рационального поведения [48, 86] агент будет при известном стимулировании стремиться своим выбором максимизировать собственную целевую функцию (3).
Отметим, что введение дополнительного требования гарантированного обеспечения участникам АС некоторых фиксированных значений полезности не изменяет качественно результатов проводимого ниже анализа.
В рассматриваемой модели матричной структуры управления задача управления, решаемая с точки зрения РП, заключается в нахождении РП систем стимулирования, побуждающих ФР и агента выбирать такие стратегии, которые максимизировали бы целевую функцию РП (1).
Множество решений игры (множество реализуемых типов и действий) можно записать как:
(4) P(s h) = {(y’, r’) е A x W | Sy’) + h(r’) - c(y’, r’)
s(y) + h(r) - c(y, r) y е A, r е W}.
Лемма 1. s, h, y’ е A, r’ е W: если (y’, r’) е P(s, h), то (y’, r’) е P(s*, h*), где
(5) s*(y)
f s(y'), y = y'
[0, в остальных случаях ’
h (r'), r = Г
(6) h*(r)
0, в остальных случаях
Доказательство леммы 1 заключается в подстановке (5), (6) в
(4).
Содержательно, лемма 1 означает, что РП и ФР достаточно ограничиться классом компенсаторных систем стимулирования [65, 86, 87] вида (5)-(6), которые могут интерпретироваться как договора, предусматривающие фиксированные выплаты агенту за выполнение им условий договора (выбор соответствующих действий и типов).
Из (4)-(6) следует, что (у’, r’) е Р(о*, h*)
(7) о*(у’) + h*(r’) - с(у’, r’) - с(у, r) уе A, r е W.
Введем следующие предположения.
А.1. A = , W - компакт.
А.2. а) r е W min с(у, r) = 0; б) с(у, r) не убывает по у е A и
уеА
не возрастает по r е W; c0(r) не убывает по r е W.
Содержательно введенные предположения означают, что действием агента является выбор положительнозначной скалярной величины (которая может интерпретироваться как объем произведенных работ, число отработанных часов и т.д.), причем, независимо от квалификации, выбором нулевого действия агент может обеспечить себе как минимум нулевые затраты; кроме того затраты агента не уменьшаются с увеличением действия при фиксированной квалификации и не увеличиваются с ростом квалификации при фиксированном действии, а затраты ФР по повышению квалификации агента монотонны.
Из (7) следует, что в рамках предположений А.1 и А.2 для любых (у’, r’) е Р(о, h ) имеет место:
(8) о*(у’) + h*(r’) с(у’, r’).
Обсудим теперь порядок функционирования. Предположим, что сначала РП устанавливает стимулирование для ФР и агента, затем свое стимулирование выбирает ФР и, наконец, агент выбирает свои действия и типы. Таким образом, в рассматриваемой игре стратегией РП является выбор функций стимулирования о(-) и о0(-), стратегией ФР - выбор функции стимулирования h('), стратегией агента - выбор типа r и действия у.
Задача ФР заключается в максимизации собственной целевой функции (2) выбором функции стимулирования агента h(') при известном стимулировании со стороны РП. Обозначим P(o0) -множество систем стимулирования h('), на которых достигается максимум (2) при условии, что агент выбирает действия, стремясь максимизировать (3) при стимулировании (5)-(6). Справедлив следующий аналог леммы 1.
Лемма 2. О0, o*, h*, (y’, r’) e P(o*, h*): если h* e P(s0), то h* e P(Oo*), где
(9) Oo (y, r)
f oo(y',r'), y = y',r = r 0, в остальных случаях
Доказательство леммы 2 заключается в подстановке (9) в определение P(o0).
По лемме 2 РП может ограничиться классом систем стимулирования (9), в соответствии с которым он выплачивает ФР вознаграждение только в случае предоставления последним для участия в проекте агента, обладающего требуемой квалификацией и выполняющего заданный объем работ.
Лемма 3. Парето-эффективными для РП и ФР и реализующими соответствующие действия и типы агента являются платежи, обращающие (8) в равенство, то есть
(10) (y’, r’) e P(o*, h*) o*(y’) + h*(r’) = c(y’, r’).
Доказательство леммы 3 очевидно (см. также [43, 44, 91]).
Если потребовать, чтобы значения целевых функций участников системы были неотрицательны (условие индивидуальной рациональности), то получим, что (y’, r’) e P(o, h ), помимо (10), должна выполняться следующая система неравенств:
(11) o*(yr) + Oo*(y’, r’) ?H(y’),
(12) h*(r’) + co(r’) ? Oo*(y’, r’).
Отметим, что при неотрицательном стимулировании в рамках предположения А.2 агент всегда может обеспечить себе нулевую полезность, выбрав нулевое действие.
Таким образом, в соответствии с леммами 1-3 использование систем стимулирования (5), (6), (9), удовлетворяющих (10)-(12), обеспечивает реализуемость действия y’ и типа r’. Рассмотрим, какие типы и действия выгодно реализовывать РП.
Из условия задачи Ф(у’, r’) ® max следует, что долж-
(уУ),(10)-(12)
но быть выполнено:
(13) а*(у’) + О0у \ r’) = c(y’, r’) +c0(r’\
(то есть РП заинтересован в выполнении (12) как равенства), откуда следует справедливость утверждения следующей леммы.
Лемма 4. Целевая функция РП достигает максимума при реализации действий и типов агента (у , r*), определяемых в результате решения следующей задачи:
(14) (у*, r*) = arg max {H(y) - co(r) - c(y, r)}.
ye A, reQ
Интересно отметить, что в соответствии с леммой 4 реализовывать оказывается выгодно действия и типы, которые оптимальны по Парето с точки зрения всех участников АС (исследовать неэффективные по Парето равновесия мы не будем - см. [48]). Анализ (10)-(13) дает простое необходимое условие существования индивидуально-рационального и Парето-эффективного равновесия: c(y*, r*) + co(r*) H(y*), то есть эффект от участия агента в проекте не должен быть меньше суммы его собственных затрат и затрат ФР по обеспечению требуемой квалификации агента.
Вычислим следующую величину: Л = H(y*) - c0(r*) - c(y , r*).
Результаты лемм 1-4 обосновывают справедливость следующего утверждения, дающего решение задачи управления в рассматриваемой модели матричной структуры управления.
Утверждение 2. Оптимальные с точки зрения РП действия и типы агента (14) реализуются системами стимулирования (5), (6),
(9), удовлетворяющими (10)-(13). При этом значение его целевой функции равно Л.
Задача управления выше была сформулирована с точки зрения РП. В то же время, условия (10)-(14) дают нечто большее, чем решение данной задачи, а именно, они характеризуют множество стратегий участников, которые являются равновесными по Нэшу в игре РП и ФР и Парето-эффективными с точки зрения всех участников АС - РП, ФР и агента (см. условие (14)).
Множество этих стратегий (то есть стратегий, удовлетворяющих (10)-(12)) назовем областью компромисса (см. аналогии с областью компромисса в трудовых контрактах в [65] и в АС РК [44, 47, 91]).
Наличие непустой области компромисса в рассматриваемой модели, совместно с результатами [44, 47, 91], позволяет утверждать что характерной особенностью матричных структур управления является неединственность эффективных равновесных управляющих воздействий, приводящих к одним и тем же результатам деятельности управляемого субъекта.
Решением задачи управления в том виде, в котором она сформулирована выше (когда первый ход делает РП), является точка, принадлежащая области компромисса, которая наиболее выгодна для РП, то есть точка, обращающая (12) в равенство. В то же время, введение области компромисса позволяет ставить и решать и другие задачи, например, выбор состояния АС, оптимального с точки зрения ФР и др.
Рассмотрим в качестве иллюстрации следующий пример.
Пример 2. Пусть H(y) = у, с0(г) = Г, c(y, r) = y2/2r. Из (14) следует, что у = r = 1/4. Из (10)-(12) получаем, что стимулирование
(5), (6), (9) должно удовлетворять следующей системе неравенств:
(15) о* + h* = 1/8,
(16) о* + о0* ? 1/4,
(17) h* + 1/16 ? Оо*.
Область компромисса, задаваемая системой неравенств (15)-(17) и требованием неотрицательности стимулирования, затенена на рисунке 7.
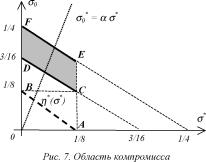
Проанализируем характерные точки рисунка 2. Прямая AB отражает зависимость h (s), получающуюся из условия (10) (в рассматриваемом примере - (15)), которое гласит, что руководители должны компенсировать затраты агента. Область компромисса, лежащая между прямыми CD и EF показывает, что диапазон суммарных выплат РП функциональному руководителю и агенту лежит между 3/16 и 1/4. Выигрыши РП и ФР при этом равны соответственно 1/16 и 0.
Если РП устанавливает правила игры, то есть делает ход первым, сообщая свои стратегии ФР и агенту, то он заинтересован в минимизации собственных выплат (ему выгодна прямая CD). Следовательно, у него есть две альтернативы - самому оплатить все затраты агента и стоимость изменения его квалификации ФР (точке C соответствуют платежи SC* 1/8, S 0C 1/16), либо выплатить ФР сумму s 0D 3/16, обязав его компенсировать затраты агенту (точка D). Если правила игры устанавливает ФР, то есть он делает ход первым, сообщая свои стратегии РП и агенту, то он заинтересован в минимизации собственных выплат (ему выгодна прямая EF). Следовательно, у него есть две альтернативы, отличающиеся от альтернатив РП тем, что прибыль остается у ФР.
Выигрыши РП и ФР при этом равны соответственно 0 и 1/16. Другими словами, ФР и РП делят полезность 1/16 и эту прибыль получает тот, кто делает ход первым (см. также [43, 65]). -
Наличие области компромисса, то есть целого множества возможных эффективных взаимодействий РП и ФР, свидетельствует о присутствии возможности управления системой, состоящей из РП, ФР и агента, поэтому исследуем роль вышестоящих органов.
Как отмечалось выше, в управлении проектами РП использует агента, подчиненного ФР, как ресурс, следовательно, необходимо исследовать возможные формальные взаимодействия между ними.
Область компромисса, задаваемая неравенствами (10)-(12), задает ту область возможных значений, относительно которой РП и ФР могут вести переговоры. Фактически, им необходимо придти к договоренности о том, как распределить между собой прибыль, равную (см. также механизмы распределения ресурса в распределенных системах принятия решений [44])
D = H(y*) - C0(r*) - c(y*, r*).
Если один из руководителей (РП или ФР) наделен правом сделать первый ход и предложить партнеру некоторый дележ прибыли, причем партнер вынужден либо согласиться, либо отказаться от участия в АС, то решение однозначно и дается (для ФР, делающего ход первым справедлив результат, аналогичный утверждению 2, с тем лишь отличием, что системы стимулирования (5), (6) и (9) должны удовлетворять неравенствам (10) и (12), а неравенство (11) должно быть выполнено как равенство). Если партнер может выдвинуть контрпредложение, то необходимо исследовать динамику процесса переговоров [105], вводя дополнительные предположения о стратегиях их участников (при этом все предложения должны оставаться внутри области компромисса).
Ситуация усложняется, если РП и ФР не могут придти к договоренности. Тогда необходимо вмешательство вышестоящих органов управления (обладающих правом приоритетного хода, то есть правом навязывания правил игры, по отношению к обоим рассматриваемым руководителям).
Примером может служить фиксация параметров договора между РП и ФР: например, обязательство РП осуществлять выплаты ФР пропорционально выплатам агенту (s0 = a s, a 0), что, однако, не делает решение единственным -см. рисунок 7, или распределение прибыли D пополам между РП и ФР, что также не делает решение единственным, и т.д.
Помимо отмеченной выше роли вышестоящего руководства, заключающейся просто в помощи достижения компромисса между РП и ФР, то есть непосредственном подсказывании или навязывании конкретной точки внутри области компромисса, вышестоящее руководство имеет также возможность: путем стимулирования РП и/или ФР изменить их предпочтения, изменив тем самым и область компромисса; навязать конкретное решение, являющееся оптимальным с точки зрения общесистемных критериев и т.д.
Итак, в настоящем разделе рассмотрена модель матричной структуры управления, в которой учитывается взаимодействие между руководителями проектов и функциональными руководителями. Получено решение задачи управления (утверждение 2) и охарактеризована область компромисса - множество таких стратегий руководителей, которые являются равновесными и Парето-эффективными.
Исследована роль вышестоящих органов управления в обеспечении эффективного функционирования АС в целом.
Перспективными направлениями исследований представляются: поиск равновесных стратегий в режиме конкуренции ПМ и ФР, исследование возможности образования коалиции между ними (по аналогии с тем как это делается в [47] для АС РК, а также изучение управляемости рассматриваемой АС с точки зрения целей и предпочтений систем более высокого уровня иерархии.
МЕТОД НЕЧЕТКОГО КРИТИЧЕСКОГО ПУТИ
Рассмотрим проект, состоящий из набора операций (работ). Технологическая зависимость между операциями задается в виде сети (сетевого графика), то есть ориентированного графа (V, E), \V\ = m, без контуров, в котором выделены два множества вершин -входы сети и выходы сети. При этом дуги сети соответствуют операциям, а вершины - событиям (моментам окончания одной или нескольких операций). В четком случае для каждой операции (i; j) задана ее продолжительность tj.
Методы описания и исследования сетевых графиков изучаются в теории календарно-сетевого планирования и управления (КСПУ) [23, 31, 41, 45, 51].
Опишем классический (четкий) метод критического пути (critical path method - CPM). Легко видеть, что продолжительность проекта определяется путем максимальной длины, называемым критическим путем.
Операции, принадлежащие критическому пути, называются критическими. Остальные (некритические) операции имеют резерв времени, характеризуемый максимальной задержкой операции, при которой продолжительность проекта не изменяется. Критические операции имеют нулевой резерв.
Приведем соответствующие формулы.
Для сети всегда существует правильная нумерация (такая, при которой из вершины с большим номером не идет дуг в вершины с меньшими номерами). Поэтому будем считать, что события занумерованы таким образом, что нумерация является правильной.
Предположим, что выполнение комплекса операций (проекта) начинается в нулевой момент времени. Обозначим Q0 - множество событий, не требующих выполнения ни одной из операций, то есть входы сети; Qi - множество событий, непосредственно предшествующих событию i, то есть множество вершин j сети, для которых существует дуга (j; i).
Положим
(1) t- = 0, i е Qo; t- = max (t- + t,¦) i e V \ Qo.
j^Qi
Величина tt называется ранним моментом (временем) свершения
i-го события и характеризует время, раньше которого это событие произойти не может. Длина критического пути
(2) T = max t-
isV
определяется ранним временем свершения конечного события, то есть события, заключающегося в завершении всех операций.
Поздним моментом t+ свершения события называется максимальное время его наступления, не изменяющее продолжительности проекта. Обозначим Ri - множество событий, непосредственно следующих за событием i, то есть множество вершин j сети, для которых существует дуга (i;j). Вычислим для каждой вершины-события i длину li максимального пути от этой вершины до выхода сети - события, заключающегося в завершении всего комплекса операций (для выходов сети считаем соответствующие величины равными нулю):
(3) U = max (lj + tj), i e V.
j^Ri
Положим t+ = T - li, i e V.
Полным резервом Ati события i называется разность между его поздним и ранним моментами свершения, то есть
(4) Ati = t+ - t-, i e V.
Итак, мы описали простейший (базовый вариант) метода критического пути, соответствующий случаю, когда имеется полная и точная информация о продолжительностях операций. Однако, во многих реальных ситуациях такая информация отсутствует, то есть имеет место неопределенность.
В зависимости от имеющейся информации различают интервальную (известен диапазон значений продолжительностей операций), вероятностную (известно распределение вероятностей продолжительностей операций) и нечеткую (имеется нечеткая информация относительно продолжительностей операций) неопределенность.
При вероятностной неопределенности в общем случае невозможно (исключение составляют операции, выполняемые последовательно или параллельно) получение аналитических выражений для распределений вероятностей и других характеристик событий проекта, поэтому для исследования свойств критического пути применяют методы имитационного моделирования - Монте-Карло и другие, реализованные в современных программных комплексах управления проектами. Мы остановимся на анализе интервальной и нечеткой неопределенности, то есть случаев информированности, при которых возможно получение аналитических выражений для параметров событий, что, несомненно, чрезвычайно привлекательно с точки зрения задач принятия управленческих решений.
Сначала обобщим рассмотренную модель на случай интервальной неопределенности относительно продолжительности операций, а именно, будем считать, что t- е [ t-, tj ], i, j e V.
Тогда ранние моменты ti свершения событий принадлежат отрезкам А- = [ t-, t- ], где
(5) t-- = t- = 0, i е Qo; t = max (t-- + t-),
JeQi
t- = max (t-+ + t j), i e V \ Q0.
1 JeQt J ]l’ *0
Длина критического пути принадлежит отрезку D = [T-; T+], где
(6) T- = max t--, T = max t-+.
ieV ieV
По аналогии с (3), вычислим для каждой вершины-события i оценки [/Г; lг+ ] длины максимального пути от этой вершины до
выхода сети - события, заключающегося в завершении всего комплекса операций (для выходов сети считаем соответствующие величины равными нулю):
(7) l- = max (lj + t- ), lj = max (Ij + t-), i e V.
JeRi JeRi
Положим tj~ = T- - lT, tj+ = T+ - lj, i e V.
Получаем следующую оценку границ отрезков, которым принадлежат полные резервы событий: (8) D ti = t\ - ti , D t+ = t+ - t+ , i e V.
В интервальной модели, в отличие от классической, нельзя однозначно сказать является ли событие критическим. Все операции могут быть разделены на три класса.
В первый класс попадают события, для которых имеет место полная определенность, то есть, события, для которых обе границы (8) равны между собой и равны нулю. Эти операции можно с полным основанием назвать критическими.
Во второй (промежуточный по степени критичности) класс попадают события, для которых нижняя граница отрезка полных резервов равна нулю, а правая строго положительна. Такие события могут в рамках существующей неопределенности оказаться критическими.
Условно назовем их полукритическими.
И, наконец, третий класс составляют события, для которых нижняя граница отрезка полных резервов строго положительна. Такие события можно с полной определенностью отнести к некритическим.
Рассмотрим иллюстративный пример.
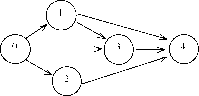
Пример 3. Пусть имеется сеть, приведенная на рисунке 8 с интервалами продолжительностей операций, приведенными в таблице
4. В таблице 5 приведены параметры событий, рассчитанные соответствии с формулами (5)-(8).
| Табл. 5. Параметры событий в примере 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Видно, что при использовании нижних границ интервалов продолжительностей операций критическими являются все события и длина критического пути T ~ = 6, а при использовании верхних границ - критическим является путь 0-1-3-4 длины T = 12. Следовательно, в условиях существующей неопределенности события 0, 1, 3 и 4 являются критическими, а событие 2 - полукритиче-ским. -
Отметим, что в предельном случае интервальной неопределенности, то есть при полной информированности, когда отрезки [ tj, tj ] - суть точки, i, j е V, выражения (5)-(8) переходят в соответствующие выражения (1)-(4).
Обобщим теперь рассмотренную модель интервальной неопределенности на нечеткий случай, при котором относительно продолжительностей операций имеется нечеткая информация jl~ (tij) ,
Hj ¦!
где Id~ (- ) : ® [0; 1] - функция принадлежности нечеткой про-
hj +
должительности операции (i, j), i, j е V.
Нечеткая информация относительно продолжительности операций может быть получена от экспертов в ситуации, когда проект и каждая операция являются уникальными (например, научные, организационные и др. проекты) и отсутствуют как нормативы, так и статистические данные.
В соответствии с принципом обобщения [14, 64, 94] функция принадлежности нечеткого раннего времени свершения /-го события, i е V, имеет вид (ранние времена свершения событий - входов сети являются четкими равны нулю):(9) m ( x)
min [ min (m ~ ( xn )); m (x.) ].
max
{(xj/). J-Q/.xj I max(xj+xj/)=x} J-Q/
J-Q/
Функция принадлежности нечеткого времени завершения проекта (нечеткой длины критического пути) есть
(іо) т~(т)
min (m ~- (X.)).
max
{(X/),i-V |min(xj ')=т} J-V
J-V j
Нечеткие длины максимального пути от вершины i е V до выхода сети (соответствующие длины для событий - выходов сети -являются четкими и равны нулю) имеют функцию принадлежности
(11) m~( x) =
min [min (m ( x.j)); m ~( x.)].
max
{(xj). j-R/,xj
max(Xj + X/i )=x} j-R/
J-R
Функции принадлежности нечетких поздних времен свершения событий имеют вид:
(12) m~+ (x) = max min [m~(T); m~(xt)], / е V.
t/ {(T, X/ ) | T - X/ = x} T l/
Функции принадлежности нечетких полных резервов событий имеют вид:
(13) m (x) = max
^ {(У/. x/ )|У/ -
Величину m = m
} min [ m~+ (y); mr (x H/ е V
X/ = x} * *
(0) е [0; 1] можно интерпретировать как степень принадлежности i-го события критическому пути, / е V.
Информация о степенях принадлежности событий критическому пути может служить для руководителей проекта индикатором, отражающим требование первоочередного внимания к событиям, у которых эти степени равны единице или близки к ней.
Отметим, что в частном случае нечеткой неопределенности -при интервальной неопределенности (то есть когда m~ (t.) = 1 и
HJ " У
Supp m(tj) = [ tj, tJj ], (/, J) е E) выражения (9)-(13) переходят в соответствующие выражения (5)-(8).
ИГРЫ С ПЕРЕМЕННЫМ СОСТАВОМ И УПРАВЛЕНИЕ ОРГАНИЗАЦИОННЫМИ ПРОЕКТАМИ
В организационных проектах, да и в проектах других типов, реализуемых в проектно-ориентированных организациях, одной из задач управления является формирование команды проекта, то есть выбор из числа сотрудников организации и/или из числа потенциальных внешних участников проекта такого их набора, реализация проекта которыми будет наиболее эффективной. Адекватной моделью этой ситуации являются рассматриваемые ниже в настоящем разделе игры с переменным составом (в которых набор игроков, принимающих участие в игре, является переменным).
Задачи формирования состава исполнителей, выбора команды проекта и т.д. близки к задачам оптимизации состава АС, решаемые в таких разделах теории управления социально-экономическими системами как: теория активных систем, теория контрактов, экономика труда, экономика организаций и др. Поэтому, прежде чем переходить к исследованию игр с переменным составом, проведем краткий обзор результатов решения задач оптимизации состава ОС.