Новоселов А.А. - Моделирование финансовых рисков
Окружающий мир полон неопределенностей, связанных с невозможностью точного предсказания будущих событий. Ошибаясь в прогнозах, мы рискуем получить не совсем то, или совсем не то, что ожидалось.
Вездесущая неопределенность является источником риска.
Математические модели, описывающие неопределенность, можно разделить на двр группы*
- вероятностные модели;
- модели нечетких множеств.
В настоящем курсе мы будем использовать только первый способ описания.
Риск
Часто нас интересует не столько исход того или иного процесса, сколько связанные с ним количественные характеристики. При этом риск может быть описан случайной величиной, или, в общем случае абстрактным случайным элементом.
Совокупность всех рисков будем обозначать X, и на начальном этапе ограничимся следующим определением.
Определение 1.1 Риском называется произвольная случайная величина.
Портфель рисков
Совокупность рисков, рассматриваемых совместно, часто обладает новыми свойствами, не присущими каждому из рисков в отдельности, поэтому введем понятие портфеля рисков V, как произвольного подмножества X.
Страхование
Под страхованием понимается передача риска от одного носителя (страхователя) другому (специализированной организации - страховой компании, страховщику) за определенную плату, называемую ценой страхования, тарифной ставкой или страховой премией. Сущность страхования заключается в перераспределении риска между многими носителями; относительно однородную совокупность рисков будем называть страховым портфелем.
Страховые портфели
Рассмотрим некоторые виды страховых портфелей, использующиеся в дальнейшем.
Простейший страховой портфель
Простейший страховой портфель
(1)
состоит из N рисков (случайных величин) X1, ...,XN, являющихся независимыми и одинаково распределенными; Х1 имеет бернуллиевское распределение
1 с вероятностью р,
О с вероятностью 1 р.
(2)
Хі
Содержательно для каждого риска страховое событие может наступить с вероятностью р, а убыток в результате наступления этого страхового события равен 1 (и одинаков для всех рисков).
Ясно, что риск портфеля
N
х = Е х
i=1
имеет биномиальное распределение с параметрами N, р:
P{X = к} = CkNрк(1 - p)(N-k), к = 0,1,N. (4)
Основные параметры этого распределения равны
EX = ^; DX = Np(1 - р). (5)
Простой страховой портфель
Простой страховой портфель
(6)
P = {Xi,...,Xn }
также состоит из N независимых рисков Xi,...,XN, однако их распределения несколько различаются:
Si с вероятностью р,
0 с вероятностью 1 р.
Xi
(7)
Содержательно для г-го риска страховое событие наступает с вероятностью р, а размер убытка в результате наступления этого события равен Si и, вообще говоря, неодинаков у различных рисков. Примером может служить страхование на случай смерти с величиной Si; определяемой страховой суммой г-го договора портфеля.
Распределение риска портфеля (3) в данном случае уже не имеет столь простого выражения, как (4), но его основные параметры все еще легко вычисляются:
(8)
EX = NpSN; DX = ^(1 p)S2N,
где
N N
-1^ Si; SN = N-1? Si2.
(9)
i=1
i=1
Реальный страховой портфель
Реальный страховой портфель является дальнейшим усложнением простого портфеля; здесь допускаются произвольные размеры убытков из диапазона [0, Si]. Формальное описание этого портфеля таково: он состоит из N независимых рисков
P = {X1,...,Xn }, (Ю)
вероятность наступления страхового события по г-му риску по-прежнему равна р, а размер убытка, вызванного страховым событием описывается случайной величиной
Xi CiriSi;
где
с вероятностью р, с вероятностью 1 р
есть индикатор наступления страхового события по г-му риску, Si - страховая сумма (ответственность) по г-му риску, a r1, ...,rN - совокупность независимых одинаково распределенных случайных величин с функцией распределения Fr (v) = P{r1 v}.
Здесь распределение риска портфеля также не имеет простого явного выражения, но по известным параметрам распределения r1
m = Eri, т2 = Dri (11)
нетрудно подсчитать основные параметры риска портфеля (3):
EX = pmNSN, DX = pm2N§N[1 - p + т2/m2]. (12)
Упражнение 2.1 Вывести формулы (5), (8), (12) для параметров рассмотренных портфелей.
Цена страхования
Одной из основных задач теории риска является определение цены, которую следует уплатить при передаче риска от одного носителя к другому. В страховании принято выражать страховую премию в долях от страховой суммы (ответственности) Si соответствующего риска. Таким образом, при размере премии T (одинаковом для всех рисков портфеля) абсолютный размер премии г-го риска оказывается равным TSi, а суммарная премия портфеля -
Q = TNSn . (13)
Попытаемся сначала сформулировать некоторые естественные принципы определения цены, и рассмотрим их действие на примере простейшего страхового портфеля.
Принципы определения цены
3.1.1 Принцип безрискованности
В качестве первого принципа попытаемся назначить цену так, чтобы деятельность страховой компании была безрискованной, то есть, чтобы собранных премий (13) с вероятностью 1 хватало для покрытия всех страховых убытков портфеля. В случае простейшего портфеля максимальный размер убытка портфеля равен N, а вероятность его появления: pN 0, так что для выполнения этого требования необходимо обеспечить равенство Q = TN = N, откуда T = 1, т.е. абсолютный размер премии совпадает с ответственностью по риску. Ясно, что такое страхование является совершенно непривлекательным для страхователей, и его рассмотрение лишено смысла.
Нетрудно проверить, что данный вывод справедлив и для более сложных портфелей рисков (см. упражнение 3.1). Отсюда следует вывод:
Безрискованное ведение страхового бизнеса невозможно,
и, в частности, страховая премия должна удовлетворять неравенству T 1.
Принцип справедливости
Попытаемся теперь обеспечить справедливостьпроцесса передачи рисков, т.е. эквивалентность финансовых обязательств партнеров. Поскольку размер страховой премии (финансового обязательства страхователя) детерминирован, а размер обязательства страховщика (возмещаемого страхового убытка) случаен, будем понимать равенство этих обязательств в среднем по портфелю: TN = EX, откуда, с учетом (5), T = р. Как мы увидим далее при рассмотрении процессов риска, такой размер премии является слишком малым, поскольку при многократном воспроизведении такого страхового портфеля с вероятностью 1 происходит разорение страховой компании.
Здесь проиллюстрируем этот эффект следующими соображениями. Зададимся вопросом: каков будет размер прибыли страховщика после т - кратного воспроизведения портфеля, сформированного по справедливому принципу. Прибыль j-ro портфеля представляет собой случайную величину Z= Q Xс EZ= 0 и D Z(j = а2 0. Поэтому искомая прибыль есть
Zm = Е Z(j) j=1
причем EZm = 0 и (в случае независимости портфелей) DZm = та2, т.е. прибыль m портфелей в среднем равна 0, но неопределенность в ее значении возрастает с ростом т, в частности, может достигнуть сколь угодно малого значения, приводя к разорению компании.
Таким образом, премия должна удовлетворять неравенству T р. Для более сложных портфелей (см. упражнение 3.2) вывод звучит следующим образом: премия должна превосходить размер среднего относительного убытка портфеля E(X/R), где R = Y^ Si - суммарная ответственность по портфелю.
Принцип достаточного покрытия
В предыдущих пунктах мы убедились в том, что первые два принципа исчисления премии неработоспособны, и следует искать другие принципы, приводящие к значениям T е (р, 1) (для простейшего портфеля). Здесь рассмотрим принцип достаточного покрытия, сущность которого заключается в следующем: поскольку единичную вероятность покрытия будущих убытков портфеля X премиями Q обеспечить не удается, попытаемся обеспечить заданное значение этой вероятности: зафиксируем число а е (0,1) и будем определять премию T из уравнения
(14)
P{X Q} = а.
Пусть F - функция распределения риска портфеля: F(x) = P{X x}, F0 - функция распределения соответствующей центрированной и нормированной случайной величины (X EX) Д/DX. Тогда уравнение (14) приводится к виду
(15)
Fo ((Q EX )/у/Ш)
откуда, с учетом (13), (5), получаем
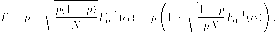
В случае большого объема портфеля N ссылка на центральную предельную теорему позволяет переписать (16) в виде
Р(1 - Р)
N
Ф-1 (а)
Ф-1(а)
(17)
pN
где Ф - функция стандартного нормального распределения.
Из (15) с использованием (8), (12), аналогично получаем выражения страховой премии для простого
Sn Р(1 Р) р-і.
SN 1 Ргр-lf \
Fo (а)
(18)
и реального
Sn ' Р( 1 Р + т2/m2) -1 / Sn 1 Р + т2/m2 -і
Fo (а) I (19)
T = Р + S-Sn
портфелей, соответственно. Здесь функция распределения F0 также может быть при большом объеме портфеля заменена на функцию стандартного нормального распределения.
Отметим, что именно формула (19), полученная нами здесь с использованием исключительно элементарных средств, рекомендована российским страховщикам нормативными документами [1] для расчетов страховой премии по всем видам страхования, отличным от страхования жизни (причем с заменой множителя 'Sn/Sn на произвольно выбранную постоянную 1.2). Вся излагаемая дальше теория еще ждет своего применения в практике российского страхового рынка.
Неоднородность портфеля
Простейший страховой портфель является вполне однородным, а в простом и реальном допускаются различные величины страховых сумм S*, что приводит к неоднородности этих портфелей. Указанная неоднородность количественно определяется коэффициентом
np = Sn/Sn . (20)
Изучим здесь его возможные значения.
Предложение 3.1 Значения коэффициента неоднородности портфеля (20) лежат в интервале [1, vN].
Доказательство. Для удобства будем рассматривать значения np и покажем, что они лежат в [1, N].
Рассмотрим вспомогательную дискретную случайную величину C, принимающую значения S1,..., SN с вероятностями N-1. Для нее, очевидно, справедливо
EC = Sn , EC2 = SN,
так что
DC = SN SN 0,
0ТКуда np 1. Для нахождения верхней границы диапаз она значений np заметим, что максимизация np та неотрицательном ортанте R+ эквивалентна задаче оптимизациии покажем, что ее экстремальными точками могут быть только единичные орты RN, т.е. векторы вида S = (0,..., 0,1, 0,..., 0) с единицей на г-ш позиции (для каждого такого вектора, очевидно, f(Si,...,Sn) = 1). Действительно, пусть решением задачи (21) - (23) является точка S(0), некоторые координаты sj0),sk0) которой удовлетворяют неравенствам 0 Sj0) S(0) 1. Ввиду симметрии задачи можно считать
j к. Тогда при достаточно малых 5 точка S(1) = (..., Sj0 5,..., Sj:0 + 5,...) является допустимой в этой задаче иf (S(1)) f (S(0)) = 25(s?0) sj0)) + 252 0,
что противоречит экстремальности S(0). Значения же квадрата коэффициента неоднородности на единичных ортах равны, очевидно, N, что и требовалось, о
Упражнение 3.1 Показать для простого и реального портфелей, что принцип безрискованности дает значение цены страхования T =1.
Упражнение 3.2 Применить принцип эквивалентности к простом,у и реальному портфелям,. Показать, что страховая, премия должна превосходитъ разм,ер средних относительных убытков портфеля.
Упражнение 3.3 Датъ геометрическую интерпретацию доказательства предложения 3.1.
Введение в теорию полезности
Риск есть состояние неопределенности, неполной информации относительно каких -либо событий в будущем. Чаще других для математического описания неопределенности используются следующие два способа:
- вероятностное описание;
- нечеткие (размытые) множества.
Второй способ предназначен для описания неопределенностей, присущих высказываниям на человеческих (неформализованных) языках.
Мы будем рассматривать только первый способ и, таким образом, определим риск, как состояние вероятностной неопределенности: будущие события нельзя предсказать точно, однако известно их вероятностное распределение.
В простейших случаях множество будущих событий конечно и риск представляется вероятностным распределением на конечном пространстве элементарных событий.
Пример 4.1 В эксперименте с подбрасыванием, монеты мы не можем точно предсказать исход этого эксперимента, однако множество всех возможных исходов конечно: О = {г,р} и известно вероятностное распределение на этом, множестве: каждый из исходов может появиться с вероятностью 1/2.
Часто нас интересуют не столько сами исходы эксперимента, сколько связанные с ними количественные значения; в этом случае риск описывается распределением некоторой случайной величины.
Пример 4.2 В условиях предыдущего примера монета может подбрасываться в процессе игры двух лиц, в которой первый игрок выигрывает или проигрывает единицу в зависим,ости от выпавшей стороны, монеты. Здесь риск описывается дискретной случайной величиной, принимающей значения ±1 с вероятностями 1/2.
Пример 4.3 Доходность финансового вложения в фиксированную ценную бумагу не может быть точно предсказана, заранее, однако всевозможные значения этой доходности могут быть описаны, случайной величиной с распределением,, полученным, статистическими методами по данным, о прошлом, поведении доходности данной ценной бумаги.
В более сложных случаях риск может описываться распределением случайного вектора, или, вообще говоря, распределением произвольного абстрактного случайного элемента; приведем строгое определение.
Пусть (О, Fb, P) - вероятностное пространство, (?, F) - измеримое пространство, где Fb, F - а-алгебры событий на О, ?, соответственно. Напомним, что случайным элементом ? на (О, Fb, P) со значениями в (?, F) называется измеримое (относительно пары а-алгебр Fb, F) отображение ? : О ^ ?.
Определение 4.1 Риском называется произвольный случайный элемент.
Пример 4.4 Пусть ? = R - вещественная прямая, F = B - а-алгебра, борел,веских множеств на R, тогда, риск есть случайная величина.
Пример 4.5 Пусть ? = Rn п-мерное пространство, F = B - а-алгебра, его борел,веских множеств, тогда, риск есть случайный вектор.
Пример 4.6 Пусть X - произвольное конечное множество, ? = 2х - совокупность всех его подмножеств, Fq - алгебра, всех подмножеств ?, тогда, ? есть случайное конечное абстрактное множество.
Вероятностное пространство (О, F, P) будем трактовать, как окружающую среду, а измеримое пространство (?, F) - как пространство результатов. Каждый случайный элемент ? порождает на (?, F) вероятностное распределение по правилу
P(T) = P{x ? О : ?(ш) ? T} = P{?-1 (T)}, T ? F, (24)
превращая его тем самым в вероятностное пространство (?, F ,P)- Будем обозначать P совокупность всех таких вероятностных рас пределений на (?, F )-
Упражнение 4.1 Приведите прим,ер нечеткого высказывания.
Упражнение 4.2 Приведите другие примеры рисков.
Упражнение 4.3 Совпадает ли совокупность распределений P с множеством всевозможных вероятностных распределений на, (?, F) ?
Предпочтения
4.2.1 Отношение предпочтения
Определение 4.2 Отношение У на произвольном множестве Y называется отношением предпочтения, если оно рі) полно, т.е. Ух, у Е Y верно x У у или у У х; р2) транзитино, т.е. х У у, у У z ^ х У z.
Пример 4.7 Частным, случаем, отношения предпочтения является отношение полного упорядочения , удовлетворяющее аксиомам
01) Ух, у Е Y верно х у или у х (полнота);
02) х у, у z ^ х z (транзитивность);
03) х у, у х ^ х = у (антисимметричность).
Видно, что, в отличие от отношения порядка, отношение предпочтения не обладает, вообще говоря, свойством антисимметричности, т.е. из х У уиу^хне вытекает равенство х и у. Будем в этом случае называть х, у одинаково предпочтительными или эквивалентными и использовать для обозначения этого факта символ
х У у, у У х =^ х ~ у.
Замечание 4.1 Отметим здесь следующий факт: отношение одинаковой предпочтительности является в строгом, смысле отношением, эквивалентности, т.е. обладает свойствами, рефлексивности х ~ х, Ух Е Y, транзитивности х ~ у, у ~ z ^ х ~ z и симметричности х ~ у ^ у ~ х, причем порожденное им, фактор -множество У = Y/ ~ является вполне упорядоченным, множеством с отношением, порядка, У, индуцированным отношением предпочтения У на, Y: для Y1,Y2 Е У отношение Yi У Y2 означает, что для некоторых (и, тем, самым, для произвольных) уі Е Yi, у2 Е Y2 выполняет ея у1 У у2.
Если же х предпочтительнее у, а обратное неверно, то будем использовать символ строгого предпочтения У:
х У у, у У х =^ х У у.
Разумный индивидуум имеет четкое представление о системе своих предпочтений на пространстве результатов ?: для произвольной пары ?1,?2 Е ? он может вполне определенно сказать, какой из этих элементов является для него более предпочтительным, или же эти элементы эквивалентны. Если результаты (элементы ?) трактуются, как доходности, то ? является подмножеством вещественной оси и отношение предпочтения можно задавать с помощью обычного отношения порядка на множестве вещественных чисел.
В теории полезности делается более сильное предположение: индивидуум имеет систему предпочтений и на пространстве распределений V, т.е. для каждой пары распределений P1, P2 Е V может определенно указать более предпочтительное для него распределение или утверждать их эквивалентность. Таким образом, на V постулируется существование отношения предпочтения У. Замечательнейшим фактом теории полезности является существование (при некоторых вполне естественных предположениях) функции полезности, адекватно описывающей это отношение предпочтения.
Упражнение 4.4 Верно ли Ух G Y : x У х?
Упражнение 4.5 Показать, что отношение У, введенное на У в замечании Jhl, действительно является отношением порядка на У.
Теорема о существовании функции полезности
4.3.1 Система аксиом
Введем на P операцию смеси распределений: для произвольных Pi, P2 G P и числа a G [0,1] смесью P1 и P2 назовем распределение P G P, задаваемое соотношением
P(C) = aPi(C) + (1 - a)P2(C), C GC.
Будем предполагать выполненной следующую систему аксиом.
А1) На P существует отношение предпочтения У.
А2) Если P1 P2, то
АЗ) Если P1 У P2, to
A4) Если P3 У P2 У P1; то существуст a G (0,1) такое, что
Приведенные аксиомы можно трактовать, как требования наличия у отношения предпочтения некоторой регулярности, правильности.
4.3.2 Теорема существования
Прежде чем формулировать основную теорему, докажем несколько лемм.
Лемма 4.1 Пусть выполнены аксиомы А1-А4, P3 У P1 и P3 У P2 У Pk Тогда существует единственная постоянная a G [0,1] такая, что
P2 - aP1 + (1 a)P3. (28)
Доказательство. Заметим, что если P3 у P2 Pb то соотношение (28) выполняется при единственном значении a = 1 (см. упражнение 4.6).
Аналогично, если P3 P2 У P15 то (28) выполняется только при a = 0 (см. упражнение 4.7).
Пусть теперь P3 У P2 У P^ Тогда по аксиоме А4 существует a1 G (0,1) такое, что выполнено
Предположим, что такое 1 неединственно, и существует а2 ? (0,1), для которого
(30)
(31)
(32)
(33)
P2 ~ 2Рі + (1 2)Рз. Положим для определенности 0 а1 а2 1. Тогда
2 аі 1 2
Рз = Д2-1 Рз + -2 Рз
1 а1
1 а1
, -Г 2 і 1 2
2Рі + (1 2)Рз = іРі + (1 1) -Рі + --Рз
.1 а1
1 а1
Поскольку Рз У Р1; по аксиоме АЗ и (31) получаем
2 1 1 о 2 Ді 1 2 _
Рз = ^-1 Рз + -2Рз у -1 Рі + -2Рз.
1 1 1 1 1 1 1 1
Отсюда с использованием аксиомы АЗ и (32) получаем:
2 і 1 2-.-.
2 1 Рі + --2 Рз
А іРі + (1 і)Рз. (34)
2Рі + (1 2)Рз іРі + (1 і)
1 1
1 1
Это соотношение противоречит (29),(30), так что постоянная 1, для которой выполнено (29) - единственна, о
Лемма 4.2 Если выполнены аксиомы А1-А4, Рз А Р'2 А Р2 А Р1 м (Р2),
' (Р2) таковы, что
(35)
Р2 ~ Рі + (1 )Рз, Р2 ~ Рі + (1 )Рз, то ' (монотонность операции смешивания)
Доказательство. Пусть, напротив, '. Тогда, по аксиомам АЗ, А4 имеем:
Р2 ~ 'Рі + (1 о')Рз
_ 1 '
Р і + і-Г'Р з
1 '
Рі + ^-::Рз
+ ( )Рі А
+ ( )Р з
1 + '
Рі + (1 )Рз ~ Р2,
так что Р2 У Р'2 - противоречие. о
Теорема 4.3 Если выполнены аксиомы .1 / Л/,, то существует вещественнозначная функция U : ? ^ R, называем,ая функцией полезности, и такая, что для произвольных Р1, Р2 ? V соотношение Р2 А Р1 эквивалентно
EU(~і) EU(S2), (36)
где Д, S2 - случайные элементы, задающие распределения Р1, Р2 ? V, соответственно. Более того, функция U единственна с точностью до положительного аффинного преобразования.
Замечание 4.2 Теорема фЗ позволяет в качестве средства для сравнения рисков ? по предпочтительности использовать их ожидаемую полезность
u(?) = EU (?).
Доказательство теоремы 4.3 проведем в предположении конечности множества результатов: ? = ($i,...,0N). При этом каждое распределение P G P можно представить вектором P = (p1, ...,pN), так что Р{?*} = pi, i = 1, Рассмотрим рас
пределения P1 = (1, 0,0) P2 = (0,1,0), ..., PN = (0, 0,1). Без ограничения общности можем считать, что
Pn h ... У Pi. (37)
Если P1 г iP 2 *** PN, то утверждение теоремы тривиально (см. упражнение 4.8), поэтому сразу считаем PN у Pb Пусть A1,AN - произвольные постоянные с A1 An зададим U(?1) = А1; U(BN) = AN. Обозначим ai, i = 1,..., N те (по лемме
4.1 однозначно определенные) постоянные, при которых
Pi - aP 1 + (1 - ai)PN, i = 1, ...,N. (38)
Ясно, что a1 = 1, aN = 0. Определим
U(?і)= Ai = aiA 1 + (1 ai)An, i = 1,...,N. (39)
Покажем теперь, что так определенная функция U обладает свойством (36). Для произвольного распределения P = (p1, ...,pN) G P, как нетрудно заметить PN У P У P1 (см. упражнение 4.9), так что мы можем задать a(P) как (однозначно определенную) постоянную из [0,1], для которой
P - a(P)P1 + (1 a(P))PN. (40)
Из леммы 4.2 вытекает, что P' У P тогда и только тогда, когда a(P) a(P'). Из (38) имеем:
N N
P = J2 PiPi Pi [aiP 1 + (1
i=1 i=1
1 J2 PiaJ Pn.
(41)
i=1
Сравнивая (40) и (41), видим, что
N
a(P) = J2 PMi-
i= 1
Таким образом, P' У P тогда и только тогда, когда
N N
(42)
J2piai 13 Piai
i=1 i=1
Из (39) вытекает, что ai = (An Ai)/(AN A1); подставляя это в (42), заключаем, что P' У P тогда и только тогда, когда
^ / AN Ai ^ N AN Ai
2^Pia-T - Pi a-
i=1 An A1 i=1 An A1
или, что эквивалентно,
N N N N
Ai 13PiAi p'iU(?) 13PiU(?3
i=l
i=l
i=l
i=l
и (36) доказано.
Осталось показать, что U определено единственным образом с точностью до положительного аффинного преобразования. Пусть U* - другая функция полезности, удовлетворяющая (36). Обозначим А* = U*(?і), i = 1,..., N из (36) и (39) имеем:
U*(?і) = aiU*(?і) + (1 - ai)U*(?і),
откуда
AN - A* = An - Аг AN - A* An - Ai ’
так что
(AN - A*)An + AN - A* A An - Ai + An - Ai i
an - Ai An - Ai
A.
(an
Ai)
A*
an
A*
an
Таким образом, U* действительно является положительным аффинным преобразованием от U. о
Упражнение 4.6 Доказать, что в условиях леммы 4-1 условие P3 - P2 ~ Pi влечет выполнение (28) при единственном, значении a = 1.
Упражнение 4.7 Доказать, что в условиях леммы 4-1 условие Р3 ~ Р2 X Pi влечет выполнение (28) при единственном, значении a = 0.
Упражнение 4.8 Доказать, что если, в условиях теорем,ы 4-3 Pi iP 2 гч' ... гч' P N,
то ее утверждение справедливо.
Упражнение 4.9 Доказать, что если, в условиях теорем,ы, 4-3 справедливо (37), то для, произвольного распределения, P Е? имеет место PN У P У Pi.
Решения
Введем теперь в рассмотрение активного индивидуума. Пусть A обозначает множество его действий (решений), и поведение системы в целом описывается функцией X : Ах О ^ ?, измеримой относительно и при каждом фиксированном а Е A (т.е. {и Е О : X(а, и) Е F} Е F, F Е F), так что если индивидуум принял решение а Е А, а среда оказалась в (случайном) состоянии и Е О, то результатом действия а будет ? = X(а, и) Е ?.