Модели экстремальных событий
Аналогично тому, как в Фурье-анализе базисом является набор функций, полученных из базовой функции -синусоиды путем изменения частоты, так и семейство вейвлет образуется из некоторой базовой функции путем сдвигов (по времени) и изменений масштаба, что является удобным и естественным инструментом для работы с нестационарными временными рядами.
Сейчас поясним эту идею, а более детальное изложение теории вейвлет приведено в приложении 1, а также в работах [8, 9].
Разложение по вейвлетам в дискретном случае имеет вид
-1 T-1
r = XX wik?ik(t X (14)
j=- J k=0
где у'jk - базис, образованный вейвлетами, j - индекс масштаба, к - индекс
локализации.
Аналогично эволюционному фурье-спектру (13) введем понятие эволюционного вейвлет-спектра
Это выражение дает вклад, вносимый в общую вариацию, вейвлетом с локализацией t=k/T и масштабом j. Таким образом, у нестационарного процесса вариация, зависящая от времени, является суммой по всем масштабам:
В работах [8, 9] показано, что для стационарных процессов понятие локальной вариации совпадает с понятием обычной вариации, а также что в пределе Т^^ локальная вариация стремится к вариации обычной. Эволюционный вейвлет-спектр находится с помощью дискретного стационарного вейвлет-преобразования (см. приложение 1), алгоритм которого, удовлетворяющий нужным условиям, был разработан и приведен в работе в приложении j.
Для наших задач в дальнейшем мы будем использовать оценку вариации
o(t), полученную посредством вейвлет-анализа, для вычисления VaR методом вариаций-ковариаций.
1.3. Модели экстремальных событий
Нормальное распределение, как следует из центральной предельной теоремы, хорошо подходит для описания центральной части распределения сумм независимых одинаково распределенных случайных величин. Для нахождения больших квантилей (т.е. значений VaR для значений уровня достоверности, скажем, больших 99%) применяется теория экстремальных значений в статистике (Extreme Value Theory - EVT) [1, 10, 11].
Математически это формулируется следующим образом. Пусть
(Х,..., Xn) - выборка независимых одинаково распределенных случайных
N(0,1) при n ^ ^ .
величин. Тогда согласно центральной предельной теореме {(X1 +... + Xn )n-V]
Задачей теории экстремальных значений является нахождение распределения не суммы, а минимума (или максимума), т.е. такой функции
G(x), чтоin{X1 Xn}- bna„
где {an } и {bn } - некоторые числовые последовательности.
Согласно теории экстремальных значений функция G(x) может относиться к одному из нескольких семейств распределений, среди которых чаще всего используются следующие.
| Название | Функция распределения, F(x) |
| Обобщенное распределение экстремальных значений (General Extreme Value distribution). | Г 1 1 , Л |
| t (1 + 7xr\, 1 Yx | |
| Распределение Парето, или степенной закон | 1 - x_a, x 1, a 0 |
| Распределение Вейбулла (Weibull). | 1 - exp[-AxTJ, x 0, X 0, t 0 |
Для остальных распределений получить оценку VaR в аналитическом виде крайне затруднительно, поэтому они используются в основном в методе Монте-Карло.
Для преодоления этих затруднений, в работе [10] предложен новый метод, сочетающий удобство метода вариаций-ковариаций с сохранением свойств хвостов распределений. Идея состоит в нелинейном преобразовании исходной случайной переменной в случайную переменную, имеющую нормальное распределение. Далее вычисляем значение VaR для новой переменной, используя любой из методов вариаций-ковариаций, описанных выше.
Затем для вычисления распределения прибыли/убытков портфеля в исходном пространстве используются методы, применяемые в теоретической физике.
Данный подход заключается в следующем. Пусть доходности ri(t) имеют кумулятивную функцию распределения F(r,).
Введем преобразование ri ^ yi, преобразующее распределение F(r) в стандартное нормальное распределение. Из статистики известно, что такое преобразование можно найти из следующего соотношения:
Уі_
?2
1 + erf
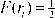
где erf - функция ошибок (erf(х) = [ e и du).
J 0
В явном виде преобразование (20) имеет вид
(21)
Уі = V2erf-1 (2 F (r) -1).
При том, что yi имеет нормальное распределение, мы не теряем информации о характере хвостов распределения F(ri).
Преобразование (20) имеет место для любых распределений F(ri). Рассмотрим случай, когда F(ri) имеет вид модифицированного распределения Вейбулла:
2лП
I c/2-1
r
P(r) =
(22)
В этом случае с небольшим изменением нормировки выражение (21) упрощается до следующего:
С /2
Уі = sign(ri ^ ri
(23)
при котором вариация yi равна Vu = (r0 t )c .
Ковариационная матрица многомерного распределения Y = (У1,...,yn) имеет следующую оценку:
v=e[yyt J- e[y]e[yt J ,
(24)
и соответственно распределение имеет вид
-1 /2
P(Y) = (2п)-N/2 V
(25)
Xexp{-{{ -e[ytJ)V-1 (Y-E[YJ)},
где | V| - определитель матрицы V.
Чтобы получить исходное распределение P(r), используем тот факт, что
P( R) = P(Y) dd-. (26)
dR
где dY/dR - якобиан преобразования R ^ Y.
Таким образом, получаем окончательный вид
P(R) = Ivl112 exp{- { (YT - e[yt J)- -1)(Y - E[y]Vx
dF,
ХП[ dr (r)'
(27)
j=1 j
Заметим, что при использовании преобразования (23) в формуле (27) вместо единичной матрицы необходимо использовать диагональную матрицу
V, = (Го,,)
Теперь найдем распределение доходностей портфеля, состоящего из N инструментов. Доходность портфеля представляется выражением
(28)
=1
В терминах преобразованных переменных
N
(29)
R(t) = X wsign(r, )|r q , q , = 2/ c,
=1
Пропуская дальнейшие вычисления, приведем только результаты. Интересующее нас распределение доходности портфеля можно выразить посредством кумулянтов.
Кумулянты определяются следующим образом: подобно тому, как моменты /us являются коэффициентами разложения Mх (t) = E И J в ряд
Тейлора, так ks - кумулянты - являются коэффициентами разложения
ts
ln(M*(0) : \n(Mx- (t)) = x;=! к/-.
Теперь приведем полученные выражения для нескольких первых кумулянтов:
Nк1 =I wiMi(1ь
i=1
N
к2 =I w {Mi (2) - Mi (3)),
i =1
N / ч
кз = I w3 (М, (3) - 3M, (1) M, (2) + 2 M, (1)3),
i=1
N
к4 = I w* {m, (4) - 3m, (2)2 - 4Mi (1)Mi (3) +
i=1
(30)
+12 M, (1)2 M, (2) - 6M, (1)4),
где
при m = 2к, к e N;
Mt (m) =
(31)
Кумулянт к2 представляет собой вариацию доходности портфеля, так что можно использовать его для получения оценки VaR. Надо заметить, что кумулянт к4 представляет эксцесс доходности портфеля в явном виде, а так как величина эксцесса связана c вероятностями больших отклонений, то мы получаем возможность контролировать и риск экстремальных флуктуаций доходности портфеля.
1.4. Аппроксимация изменений стоимости портфеля
В рамках вариационно-ковариационного подхода можно получить аналитическое выражение для значения VaR, но лишь в тех случаях, когда функция изменения стоимости портфеля является линейной или квадратичной относительно изменений факторов риска.
1.4.1. Линейные модели
В этом классе моделей предполагается, что P(t,x) имеет производную по
каждому аргументу и высшие производные равны нулю
^dP(t, x) dP(t, x) dP(t, x) ^
градиент P,
Обозначим через g =dx1 ’ dx2dxn
который представляет собой чувствительность стоимости портфеля по отношению к изменению факторов риска. Разложим P(t,x) в ряд Тейлора в окрестности точки (t0,x0) и оставим только линейные члены ряда:
P(t,x) = P(tQ,x0) + Pt(t-10) + gT(x - x0),
откуда следует, что
AP(At, Ax) = PtAt + gT Ax. (32)
Изменения стоимости портфеля будет иметь следующее распределение:
AP - N(PAt, gTZg).
Доказательство этого факта следует из свойств нормального распределения при линейных преобразованиях.
Теперь найдем выражение для оценки VaR. По определению VaR
= a.
AP - Pt At VaR - Pt At
4TPg 4TPg, Л VaR - PtAt
Таким образом, Z (a) =-. , где Z(a) - a-квантиль нормальногоhT ^g
распределения (Z(a)=1.65 для a=0.95). Отсюда находим явную формулу для значения VaR:VaR = PtAt + Z(a)VgTZ,g. (33)
В случае, если портфель состоит только из линейных инструментов, можно получить следующий результат. Пусть at - доля инструмента i в портфеле. Тогда выражение (33) примет видVaR = ^Viai +Z (a)xl aT Za,
i
где Vi = E[ (At)] - математическое ожидание доходности i-го инструмента (как уже говорилось ранее, зачастую оно принимается равным нулю).
1.4.2. Квадратичные модели
Для нелинейных инструментов типа опционов функция AP(At, Ax) зависит от своих переменных нелинейным образом. При этом распределение AP(At, Ax) уже не будет нормальным, поэтому для нахождения процентных точек необходимо использовать другие методы, которые и излагаются ниже.
В гамма-нормальных моделях функция AP(At, Ax) аппроксимируется до второго порядка: предполагается, что P(t,x) имеет вторые производные по t и х, обозначаемые Pt, Ptt, g, Ptx и H.
p dt dP g ~ldx
и Pt =
dP _ Эdp
- скалярные величины,
dt
P =d2P
tx dtdx
ГГ d 2 P
- векторы, H- матрица nxn (гессиан): H, = -J dxdx,
1 J
Теперь рассмотрим методы вычисления квантилей.
Аналитический метод. Данный метод состоит в том, чтобы аппроксимировать распределение AP(At,Ax) распределением из определенного параметрического семейства (отличным от нормального), а затем по найденному распределению найти квантиль. Разложим P(t,x) в ряд Тейлора до второго порядка:
P(t, x) = P(t0, x0 ) + Pt At + gT Ax + 1 {HAx + 2 Px AxAt + P„ At2}. 34
Таким образом, AP(At, Ax) = P(t, x) P(t0, x0) - квадратичная
функция от вектора Ax, имеющего многомерное нормальное распределение. Воспользуемся следующими результатами статистики.
Пусть y ~ Np (v,Z), Q(y) = yT Ay + aTy + d, AT = A.
Тогда r-й момент распределения Q(y) равен
2'^v""j
J=1
2k\2(2Xjr1 + M±b](2Xj)k-l, k 1;
J=1
-2 (2Aj) + (d + aT /li + mtAm), k = 0
2 j =1
PTZ1/2 AZ112 P = diag (X1Xp) = Л, PPT = I E (Q( y)') =
(35)
где
1/2
PT(Z1 /2a + 2Z1 /2Am) = b = (bbp)T.
Для первых четырех моментов эта формула дает следующие выражения:
E (Q( у)) = = g0),
E (Q( у ))2 = М2 =
E (Q( у ))3 =Мз =
g (1)Мо +
(П
g (0Ч
g (2)Мо +
g (1)М +
g (0)М2
( 3^g(0)М3 .
(36)
Момент /и0 принимается равным единице. В наших обозначениях
у ~ N(0, Z), A = 2 H, a = (g + PttAt), d = PAt + p, (At)2.
Для функции распределения ^Ap не существует аналитического выражения, поэтому применяются различные аппроксимации, использующие разложения по более простым функциям распределения одной переменной (хи-квадрат, специальные функции и т.д.). К примеру, разложение Корниш-Фишера (Comish-Fisher) имеет следующее выражение:
Fw (а) = ф() + 6(ф(а)2 -1^ + ? (ф(а)3 - 3ф())к4 -- ? (2Ф(а)3 - 5Ф(а)),
где Ф(а) - функция нормального распределения; кз и к4 - кумулянты
распределения F^p.
Оптимизационный метод. Используя определение VaR (1), его значение можно находить как решение оптимизационной задачи. При сделанных предположениях о квадратичной функции стоимости портфеля и нормальном распределении переменных состояния оптимизационная задача примет вид
(37)
max - [p At + gT Ax + 1 AxTHAx\.
Ax: AxTE-1Ax к
Для численного решения задачи оптимизации с квадратичной целевой функцией существуют эффективные методы, например Левенберга-Маркварда. Помимо определения собственно значения VaR, решение задачи дает еще и сценарий (значения переменных состояния), при котором это значение достигается.
Однако при большом числе переменных состояния данный метод применять становится невыгодным.
Проверка гипотез о виде распределений
Исследование временных рядов при использовании методологии VaR необходимо проводить по следующим причинам.
- При выборе типа модели для факторов риска необходимо знать вид и свойства их распределений. При анализе больших квантилей необходимо также знать характер распределений экстремальных значений.
- Выбрав модель и найдя ее параметры, необходимо проверить ее адекватность реальным данным. Это особенно важно при тестировании моделей (для нахождения источников ошибок) и при их сравнении (см. разд.
3).
Приведенные в данном разделе методы позволяют определить вид функции распределения реальных данных, определить параметры искомого распределения, а также оценить степень соответствия. Вначале дадим несколько определений.
Пусть (X^..., Xn) - выборка независимых одинаково распределенных
случайных величин. Обозначим порядковую статистику через
(X*,...,ХП): X* X2 ... X*.
Пусть случайная величина X имеет функцию распределения F(x). Квантиль-функция определяется как обратная функция для F(x):
Q( p):= F(x).
Соответственно эмпирическая квантиль-функция имеет следующий вид:
Qn(p) = X* p G
І -1 І
П ’ П _
Для анализа свойств распределения реальных данных выборки удобно применять сравнительно простые графические методы, относящиеся к области непараметрической статистики и вследствие этого представляющие собой универсальное средство для проведения предварительного анализа данных.
В работе было проведено исследование статистических характеристик временных рядов для некоторых рынков. В качестве объектов исследования были взяты следующие рынки: рынок FOREX устойчивых валют (USD,DEM и пр.) в качестве примера достаточно стабильного рынка, рынок FOREX "мягких" валют (RUR,UAH,KZT) - в качестве крайне нестабильного рынка, сильно подверженного внешним воздействиям; а также рынок российских корпоративных ценных бумаг.
2.1. Графические методы
2.1.1. Квантиль-квантиль графики
Пусть F(x, ?) - некоторая параметрическая модель для функции распределения, F = F(Х,?) - модель с оцененным параметром. Тогда
квантиль-квантиль графиком (Quantile-Quantile plot) для выборки (Xi,...,Xn) назовем график
(38)
{(Q(Pk X Qn (Pk ))k = 1.-. n J, (38)
где Pk~k/(n+1), Q - теоретическая квантиль-функция для функции распределения F.
Идея использования квантиль-графиков состоит в следующем: если X и Y - две случайные переменные, связанные некоторым преобразованием g: Y = g(X). то и квантиль-функции также связаны этим преобразованием: Qy (Р) = g(QX (P)). В частности, если преобразование g - линейное, то квантиль-график представляет собой прямую.
Таким образом, квантиль-график позволяет ответить на вопрос о том, насколько подходит то или иное распределение для описания распределения выборки данной случайной переменной. Что важно, для этого не нужно находить параметры этого распределения.
Помимо этого, с помощью данного графика можно сравнить распределения различных выборок одной и той же переменной. С помощью квантиль графика можно получить также и количественную характеристику соответствия распределений, а именно ранговую корреляцию
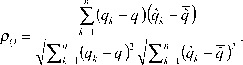
(39)
0.999, с достоверностью 95% подтверждает гипотезу о соответствии распределений.
2.1.2. Средняя функция превышения
С помощью данного метода можно более детально распознать близость хвостов распределения реальных данных к тому или иному распределению.
Средняя функция превышения (mean excess function) определяется следующим образом:e(u) = E[X
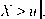
а ее эмпирический аналог имеет вид
X (X - и)+
en (и) = ^- (41)
X I{ Xi и}
i=1
где Ia(x) - индикаторная функция множества A, аy+:=max{y; 0}.
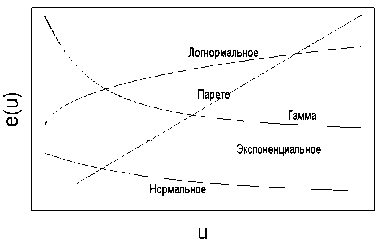
На рис. 2 приведены виды теоретических кривых средних функций превышения для некоторых распределений.
Анализируя график функции en(u), по его виду можно делать выводы о соответствии или несоответствии реальных данных тому или иному распределению.
2.2. Тесты на нормальность распределения
Большинство моделей VaR используют предположение о нормальности распределений, поэтому необходимы специфические тесты на нормальность. Основными статистиками в эконометрике, указывающими на отклонение
распределения от нормального, являются асимметрия (skewness) и эксцесс (kurtosis), характеризующие асимметрию распределения и наличие тяжелых хвостов соответственно. На значениях выборки они вычисляются следующим образом:
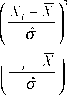
Пі=1
(42)
(43)
Для нормального распределения значение асимметрии равно нулю (как и всех нечетных моментов), а значение эксцесса равно 3. Таким образом считается, что значение эксцесса, значительно превышающее 3, указывает на наличие тяжелых хвостов у распределения.
2.3. Исследование рынков FOREX
Характеристики исследуемых рынков FOREX проиллюстрируем на примере исследования временных рядов DEM/USD и RUR/USD.
| Результаты тестов на нормальность | ||||||||||||
|
незначительно отличается от нормального. То, что эмпирические квантили больше теоретических для малых значений квантилей (левая часть графика) и меньше теоретических для больших (правая часть), свидетельствует о том, что на обоих хвостах реальное распределение тяжелее, чем нормальное. Вид эмпирической средней функции превышения также подтверждает близость к нормальному распределению (см. рис. 4).
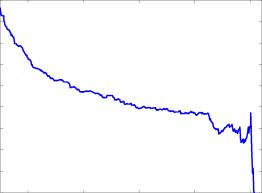
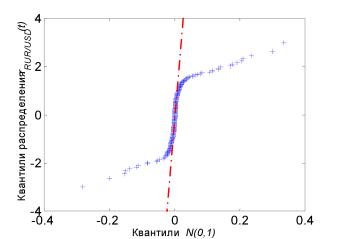
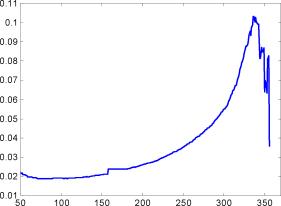
Для ряда же RUR/USD за период с августа 1998г. по декабрь 1999г. результаты тестов на нормальность свидетельствуют о том, что распределение далеко от нормального. Это подтверждает и исследование квантиль-графика (рис. 5), где уже для сравнительно небольших значений квантилей наблюдаются существенные отклонения. По характеру графика можно судить о наличии у распределения крайне тяжелых хвостов. По характеру средней функции превышения (рис. 6) можно сделать вывод о близости распределения к распределению Вейбулла. Чтобы проверить это предположение, построим квантиль-график теперь уже для распределения Вейбулла (рис. 7). Из данного графика видно, что распределение Вейбулла весьма хорошо соответствует реальному распределению для практически всех квантилей. Здесь надо заметить, что квантиль график строился только для положительных элементов выборки, так что левая часть графика - фактически центральная часть всего распределения - для анализа не используется.

2.4. Исследование российского рынка акций
Ниже приведены результаты тестов для временных рядов котировок акций РАО ЕЭС в торговой системе РТС (EESR.RTS) за период с августа 1998г. по декабрь 1999г. Результаты тестов на нормальность: асимметрия 7=0.1170, эксцесс к=4.5030, ранговая корреляция pg=0.9877.
Полученные результаты свидетельствуют о наличии асимметрии распределения и тяжелых хвостов, но не так явно выраженных, как у ряда RUR/USD. Таким образом, данный рынок занимает промежуточное положение между рынком FOREX твердых валют и мягких валют.
Этот факт подтверждают графики на рис. 8-9.
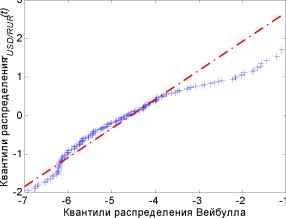
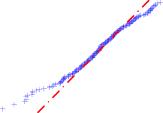
Рис. 8. Квантиль-график для акций РАО ЕЭС
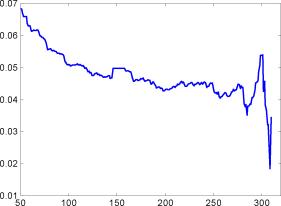
Полученные характеристики различных рынков далее будут учтены в разд. 3 при анализе применимости различных моделей вычисления VaR.
Тестирование моделей
Критерии оценки и сравнения различных моделей VaR можно условно разделить на две группы - точность модели и эффективность модели.
К первой группе относятся тесты на соответствие исследуемой модели вычисления VaR самому определению VaR (1). Поскольку определение дано в статистических терминах, то для проверки соответствия можно использовать различные статистические тесты. Так, например, случайный процесс, принимающий нулевое значение, если изменение стоимости портфеля не превышает значения VaR, и 1 - иначе, является процессом Бернулли, где событие 1 происходит с вероятностью а. Данную гипотезу можно проверить стандартными статистическими методами.
Недостатком такого подхода является то, что для проверки гипотез требуются достаточно большие тестовые выборки, которые не всегда доступны (в особенности для развивающихся рынков), а также отсутствие наглядной интерпретации результатов. Наряду с этим простые традиционные тесты, применяемые специалистами-практиками по управлению рисками, зачастую сводятся лишь к подсчету числа случаев превышения уровня VaR (при некотором уровне достоверности а) и сравнения полученного числа с теоретически ожидаемым.
Хотя такие результаты и являются наглядными, однако они не дают полной картины. По этой причине в работе приведен ряд дополнительных тестов на точность модели, предложенных в [1].
Второй группой критериев является эффективность модели. При использовании меры риска VaR для управления рисками менеджер по рискам формирует некоторую стратегию.
В качестве такой стратегии в данной работе будет рассматриваться пассивное управление рисками, т.е. стратегия, заключающаяся в резервировании дополнительных средств для покрытия возможных потерь. Размер этих дополнительных средств, называемых рисковым капиталом (risk capital), и определяется величиной VaR. Эффективность такой стратегии в принципе можно оценить единым функционалом, использующим понятие функции потерь (см. ниже), однако для этого необходимо знать множество дополнительных рыночных параметров: ставки привлечения/размещения средств, наличие штрафных санкций и т.д.
Поэтому в работе предложено использовать многокритериальные оценки эффективности, состоящие из дополненного набора тестов, предложенных в [1].
Несмотря на существенную разницу между этими двумя группами критериев, все тесты и на точность, и на эффективность, приводятся единообразно в рамках формализма функции потерь.
3.1. Методика тестирования моделей
Тестирование модели осуществляется путем прогонки по некоторой тестовой выборке (или нескольким выборкам) исторических или смоделированных данных. Таким образом, для тестирования по выбранному критерию необходимо выбрать набор тестовых портфелей и набор тестовых выборок из временных рядов.
Выбор портфелей для тестирования можно осуществлять следующими способами. Пусть мы имеем N инструментов. Тогда тестировать можно следующим образом:
1) взять N тривиальных портфелей из одного инструмента, для каждого измерить значение теста и взять среднее по всем портфелям;
2) взять один портфель из N инструментов с одинаковыми весами;
3) распределить веса инструментов в портфеле случайным образом.
Так как во всех моделях предполагается, что среднее Лг равно нулю, то на тот случай, если в тестовых выборках присутствуют тренды, проделаем процедуру симметризации, т.е. для каждого портфеля в тестовый набор включать еще и портфель с такими же по абсолютному значению весами, но с противоположными знаками (т.е. меняем длинные позиции на короткие и наоборот). При этом мы исключаем влияние трендов на значение теста.
В данной работе тестирование проводилось на различных выборках временных рядов следующих рынков: