Управление риском
Соответственно, индекс vi 0 (i ф n) равен количеству ресурса, такому что, участвуя в любой схеме с i-частью повышенного риска, элемент i отдает не более vi единиц ресурса, и существует i-часть повышенного риска, участвуя в которой элемент i отдает ровно vi единиц ресурса.
Для вершины i = 0 это очевидно (и0 = v0 = ao). Предположим, что этот факт имеет место для всех j q. Докажем его для вершины q ф n. Очевидно, что все q-части низкого риска должны заканчиваться дугами (i,q) е Uq.
Но тогда выражение (6.1) определяет максимальное количество ресурса (не более), которое отдает элемент q, участвуя в обменных схемах с q-частью низкого риска. Очевидно, что, если uq 0, то существует q-часть низкого риска, участвуя в которой элемент q отдает ровно uq единиц ресурса. Далее, все q-части повышенного риска состоят либо из i-части низкого риска и дуги (i,q) е Vq, либо из i-части повышенного риска и дуги (i,q) е иФВ обоих случаях выражение (6.2) определяет количество ресурса, не более которого отдает элемент q, участвуя в обменных схемах с q-частями повышенного риска.
Столь же очевидно, что существует q-часть повышенного риска, участвуя в которой элемент q согласен отдать ровно vq единиц ресурса. Если теперь проанализировать выражение (6.3), то по аналогии с предыдущим анализом нетрудно показать, что любая обменная схема может состоять либо из i-части низкого риска и операции (i,n) низкого риска (первое выражение в квадратных скобках), либо из i-части низкого риска и операции (i,n) повышенного риска (второе выражение в квадратных скобках), либо из i-части повышенного риска и операции (i,n) низкого риска (третье выражение в квадратных скобках).
Следовательно, un определяет максимальный доход оператора. Для определения оптимальной обменной схемы применяем алгоритм обратного хода по аналогии с алгоритмом из параграфа 5.
Пример 6. Рассмотрим сеть из примера 5, в которой все операции с обменными коэффициентами выше 2 и операция (4,5)имеют повышенный риск (эти операции изображены на рис. 14 жирными дугами).
0 шаг. uo = 4.
1 шаг. u1 = min (10, u0k01) = 8;
v1 = 0.
2 шаг. u2 = min (10, u1k12) = 10;
V1 = min (10, ufe) = 10.
3 шаг. u3 = 0;
V3 = min (18, ufe U2k23) = 18.
4 шаг. U4 = min (24, u2k24) = 15;
v4 = min (24, max (u1k14, v3k34)) = 24.
5 шаг. u5 = max (u1k15, U4k45, v3k35) = 40.
Оптимальный путь, очевидно,
m = (0, 1, 5).
Заметим, что описанный алгоритм можно обобщить на случаи, когда допускается более одной операции повышенного риска. Достаточно ввести не 2 индекса в вершине, а (m+1), где m - число операций повышенного риска, которое допускается в обменной схеме.
Управление риском
Выше уже отмечалось, что риск операций можно уменьшить, применяя различные компенсационные меры, то есть риском можно управлять. Безусловно, снижение риска требует затрат, уменьшающих доход от обменной схемы.
Рассмотрим задачу выбора оптимальной обменной схемы (по критерию дохода) с учетом затрат на снижение риска до требуемого (приемлемого) уровня.
Обозначим через затраты на снижение риска операции (i,j) до приемлемого уровня. Тогда доход оператора от реализации обменной схемы m будет равен
д = K(m)-x(m) - R(m),
где R(m) = I Гіі - суммарные затраты на снижение риска. Ограничим число
(i,j)em
операций повышенного риска (выше, чем приемлемый риск) в обменной схеме. Обозначим это число через m. Для случая m = 1 опишем алгоритм множественной индексации, обобщающий алгоритм двойной индексации, описанный в параграфе 6. Идею алгоритма поясняет рис.15.
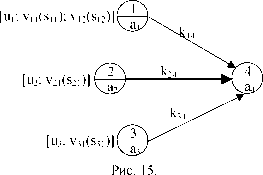
Зная индексы вершин 1, 2, 3 можно определить индекс вершины 4. Действительно,
u4 = min[a4; max(u1k14; u3k34)],
V41 = min[a4; max(u2k24; vnkM; V31k34)].
Предположим, что v41 = v11k14. Тогда s41 = s11. Далее определяем
V42 = min[a4; max(u2k24; V12k14; V31k34)].
Предположим, что v42 = u2k24 v41. Тогда, если r24 s11, то помечаем вершину 4 вторым индексом v42, s42 = r24. Действуем таким образом, пока не проверим все допустимые комбинации индексов вершин 1, 2, 3.
Пример 7. Рассмотрим сеть ВО из примера 6. Затраты на снижение риска до приемлемого уровня для операций с повышенным риском указаны в круглых скобках у соответствующих дуг (см. рис. 16).
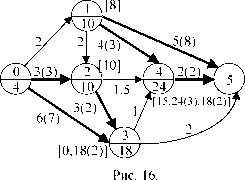
1 шаг. u1 = min (10, 4-2) = 8;
2 шаг. u2 = min (10, 8-12) = 10;
v21 = min (10, 4-3) = 10.
Так как v21 = u2, то индекс v21 не присваиваем.
3 шаг. u3 = 0;
v3 = min (18, max (4-6; 10-3)) = 18, s3i = 2.
В данном случае s31 = 2, так как обе 3-части (0,1,2,3) и (0,3) обеспечивают количество ресурса больше 18. Поэтому выбираем 3-часть с меньшими затратами на снижение риска.
4 шаг. u4 = min (24, 10-1,5) = 15;
v41 = min (24, max (8-4, 18-1)) = 24.
В данном случае s41 = r14 = 3, так как 4-часть (0, 1, 2, 3, 4) не обеспечивает количество ресурса 24, хотя и имеет меньшие затраты на снижение риска. v42 = min (24, 18-1) = 18, s42 = 2.
5 шаг. Окончательно имеем:
u5 = max (8-5-8, 15-2-2, 18-2-2) = 34.
Этот максимум обеспечивает обменная схема (0, 1, 2, 3, 5).
Этот алгоритм можно обобщить и на случай m 1. Однако система множественной индексации становится при этом излишне громоздкой.
Рассмотрим метод ветвей и границ для решения задачи управления риском. Обозначим через Q множество операций с повышенным риском и определим s = min rij. Примем, что затраты на снижение риска равны s для
(i,jQ J
всех операций множества Q и решим задачу выбора оптимальной по критерию дохода обменной схемы для этого случая. При одинаковых затратах на снижение риска задача решается методом множественной индексации, описанным в параграфе 6 (при небольшой его модификации, учитывающей затраты s при индексации конечной вершины n). Очевидно, что полученное решение дает оценку сверху для исходной задачи. Определяем в полученной обменной схеме операцию с повышенным риском и максимальными затратами на его снижение и рассматриваем два подмножества обменных схем.
В первом подмножестве эта операция присутствует в сети ВО, а во втором - нет. Сравнивая оценки сверху для обоих подмножеств, выбираем подмножество с большей оценкой и т.д., согласно схеме ветвей и границ. Дадим иллюстрацию метода ветвей и границ на сети ВО из примера 7.
Пример 8. Определяем s = min г;і= 2.
(iJQ i
1 шаг. Решаем задачу алгоритмом двойной индексации, рис.
17.
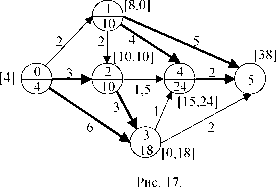
Вычитая затраты s = 2 на снижение риска операции (1,5), получаем 38. Фактические затраты на снижение риска операции (1,5) равны 8. Поэтому фактический доход равен 32.
2 шаг. Рассматриваем сеть ВО без операции (1,5) (рис.
18).
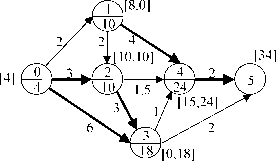
u5 = max (u4k45 - s; v3k35-s) = 36 - 2 = 34.
Оптимальная схема (0,1,2,3,5) включает операцию (2,3) повышенного риска с затратами г23 = 2 на снижение риска до приемлемого. Так как г23 = s/го полученное решение является оптимальным на множестве всех схем.
Спекулятивные обменные схемы
Спекулятивными обменными схемами называются схемы, в которых оператор выступает чистым посредником и организатором всей цепочки обменов и, в отличие от продуктовой обменной схемы, сам не имеет ресурса, участвующего в обмене. В принципе, спекулятивная обменная схема может превратиться в продуктовую, если в качестве оператора выступит один из агентов схемы, владеющий ресурсом.
Это и определяет повышенный риск спекулятивных обменных схем. Действительно, как только информация о схеме станет известна участникам (или хотя бы одному участнику), посредник (фирма-оператор) может выпасть из цепочки, и его место займет участник, реально участвующий в обмене. Такой риск превращения спекулятивной обменной схемы в продуктовую особенно велик в случае, если спекулятивная схема используется регулярно.
Наибольшие шансы занять место оператора, безусловно, имеет участник, получающий ресурс от оператора. Этого участника будем называть псевдо-оператором.
Если в задаче определения продуктовой обменной схемы требуется найти контур обмена, включающий оператора, то в задаче определения спекулятивной обменной схемы требуется найти контур обмена, не включающий оператора, а затем определить место разрыва этого контура, куда и включается посредник (фирма-оператор).
Рассмотрим сначала вторую задачу. Пусть определен контур (1,2, ... ,n,1), соответствующий замкнутому продуктовому циклу обмена с усилением контура K(m) 1. Подключение посредника-оператора к этому контуру означает разрыв контура в некоторой дуге (i, i+1) (если i = n, то n+1 = 1 по определению) и включение посредника в этот разрыв. Если обозначить оператора номером 0, то спекулятивную схему обмена можно представить в виде пути (0,i+1, ... ,n,1, ... ,i,0').
Обменный коэффициент k0,i+1 = ky+ь а обменный коэффициент kij0' = 1. Пусть допустимый поток по пути m равен x0ji+i = x(m). Тогда оператор отдает участнику (i+1) ресурс в количестве x(m), получая этот ресурс от псевдо-оператора i в количестве K(m)x(m). Доход оператора составит
До = Ci x(m)[K(m) - 1], (8.1)
где ci - доход оператора на единицу i-го ресурса. Поскольку x(m) зависит от места разрыва, то возникает задача определения места разрыва, для которого доход оператора максимален.
Обозначим Qij - усиление пути из вершины i в вершину j (Qy = K(m) по определению). Если место включения оператора в обменную схему определяется дугой, исходящей из вершины i, то максимальный поток, соответствующий количеству ресурса i-го элемента, получаемого следующим по контуру элементом через посредника-оператора, будет определяться выражением
aj
x; = min. (8.2)
j Qu
Доход оператора от организации спекулятивной обменной схемы m составит, согласно (8.1)
Д(т) = cxi(K(m) - 1).
Таким образом, оптимальное место включения оператора в схему определяется псевдо-оператором i, для которого cixi максимальна. Определить такой элемент проще всего путем перебора всех вершин контура
m.
Пример 9. Рассмотрим контур m = (1,2,3,4,5,1) из пяти вершин, данные об усилениях дуг kj ограничениях на ресурс ai и удельных доходах ci которого приведены в таблице 2. В таблице указано усиление дуги, заходящей в соответствующую вершину. Определим усиление путей Qij:
Q12 = k12 = 1; Q13 = k12'k23 = 3; Q14 = k12'k23'k34 = 6;
Q15 = k12'k23'k34'k45 = 3; Q11 = K(m) = .
Таблица 2.
| вершины | 1 | 2 | 3 | 4 | 5 |
| 4 | 1 | 3 | 2 | 0,5 | |
| Hi | 12 | 10 | 20 | 16 | 6 |
| Ci | 2 | 2 | 1,5 | 1 | 3 |
Остальные Qij определяются аналогично. Значения Qij приведены в таблице 3.
Таблица 3.
| \j i |
1 | 2 | 3 | 4 | 5 |
| 1 | 12 | 1 | 3 | 6 | 3 |
| 2 | 12 | 12 | 3 | 6 | 3 |
| 3 | 4 | 4 | 12 | 2 | 1 |
| 4 | 2 | 2 | 6 | 12 | 0,5 |
| 5 | 4 | 4 | 12 | 24 | 12 |
Согласно выражению (8.2) вычисляем:
_ ¦ /12/ . 10/ .20/ . 16/ ,6/\ -і .
x1 - min ( / 12; Л, / 3; /б, /3) - 1;
„ _ /12/ .10/ . 20/.16/.6/Ч 5/.
x2 - тіП ( /12, /12; /3; /6, /3) - /6,
12 10 20 16 6 2 x3 - min ( /4; /4; /12; /2; /1) - 1 /3;
12 10 20 16 6 1 x4 - min ( /2; /2; /6; /12; /0,5) - 1 /3;
псевдо-оператора 3 в количестве х3 = 5/3. В результате цепочки обмена (0, 4, 5, 1, 2, 3, 0) оператор получает от псевдо-оператора 3 ресурс в количестве 5/3 - 12 = 20.
Отдавая 5/3 единиц элементу 4, оператор имеет доход (20 - 5/3) -3/2 = 27,5.
Рассмотрим теперь первую задачу, то есть задачу выбора оптимального контура обмена. Ее решение сводится к перебору возможных псевдооператоров, для каждого из которых решается задача определения обменной схемы по критерию прибыли.
Рассмотрим метод решения на примере.
Пример 10. Рассмотрим сеть ВО, приведенную на рис.
19.
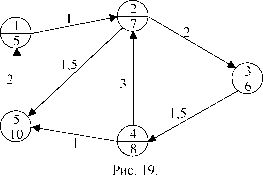
20.
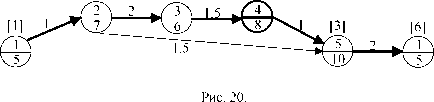
Путь с максимальным усилением m = (1,2,3,4,5,1), К = 6, поток по
нему
Хі = min (5/6; 7/і; 6/2; 8/з; 10/з) = 5/6В данном случае, в отличие от продуктовой схемы, следует учитывать ограничения на количество ресурса, которое может отдать псевдо-оператор, поскольку он отдает ресурс K1x1 реальному оператору.
Прибыль псевдо-оператора (точнее псевдо-прибыль, поскольку реально псевдо-оператор оставляет себе ресурс, полученный от участника 5, но его это устраивает, поскольку условия обмена выполнены)
П = Х1(К1 - 1) = 5/6-5 = 4‘/6.
Удаляя насыщенную вершину 4, получаем всего один путь m2 = (1,2, 5,1) с усилением К2 = 3, потоком х2 = 5/3 и прибылью 5/3-2 = 31/3.
Таким образом, оптимальный путь это путь m1. Определим для этого пути оптимальное место включения оператора. Величины коэффициентов Qij приведены в таблице 4.
Таблица 4.
| \j i |
1 | 2 | 3 | 4 | 5 |
| 1 | 6 | 1 | 2 | 3 | 3 |
| 2 | 6 | 6 | 2 | 3 | 3 |
| 3 | 3 | 3 | 6 | 1,5 | 1,5 |
| 4 | 2 | 2 | 4 | 6 | 1 |
| 5 | 2 | 2 | 4 | 6 | 6 |
Имеем:
Х1 = min (5/6
7/ - 6/ - 8/ - 10/) = 5/ - /1; '2; /3; /3) /6;
х2 = ШІП (5/6; 7/6; 6/2; 8/3; 10/з) " 5/6;
хз = min (5/з; 7/3; 6/6; 8/і,5; 10/і.5) = 1;
х = min (5/2; 7/2; 6/„; 8/б; 10/і) = 11/2; х5 = min (5/2; 7/2; %; 8/б; 10/б) = 1‘А
Примем с1 = 1, с2 = 1,5, с3 = 2, с4 = 3, с5 = 4. В этом случае maxcixi = c5x5 = 6.
i
Оптимальным для оператора является выбор в качестве псевдо-оператора участника 5. Его доход при этом составит Д0 = 6(6-1) = 30. Поскольку мы определили еще один контур m2 = (1,2, 5,1), то имеет смысл найти оптимальное место включения оператора и для этого контура. Величины Qij для него приведены в таблице 5.
Таблица 5.
| \ j i |
1 | 2 | 5 |
| 1 | 3 | 1 | 1,5 |
| 2 | 3 | 3 | 1,5 |
| 5 | 2 | 2 | 3 |
Имеем:
х1 = min (5/з; 7/і; 10/2) = 5/з; х2 = min (5/3; 7/3; 10/1,5) = 5/3; х5 = min (5/2; 7/2; 10/3) = 5/2.
Доход оператора Д0 = с5х5 (3-1) = 20.
Очевидно, что выбор в качестве псевдо-оператора участника 5 и обменной схемы (5,1,2,3,4,5) обеспечивает оператору больший доход, чем при обменной схеме (5,1,2,5). Осталось проверить последний контур m = (2,3,4).
Сразу определим оптимальное место включения оператора. Не повторяя вычислений, приведем значения xi:
х2 = 7/9; х3 = 2/3; х4 = 8/9;
шахе;х; = c4x4 = %.
i
Доход оператора До = 8/з (9-1) = 211/з.
Таким образом, оптимальной является спекулятивная обменная схема
то = (0,1,2,3,4,5,0'),
в которой оператор отдает участнику 1 ресурс псевдо-оператора в количестве 1,5, получая от псевдо-оператора этот ресурс в количестве9 единиц. Доход оператора составляет 4(9-1,5) = 30.
Методы учета и управления риском в спекулятивных обменных схемах аналогичны методам, рассмотренным при анализе продуктовых схем. Поэтому мы не будем их здесь рассматривать.
Теоретико-игровой анализ обменных схем
В этом параграфе мы рассмотрим проблемы, связанные с активным поведением участников обменной схемы. В первую очередь, активность участников проявляется в стремлении занизить величину обменного коэффициента при заключении договора об участии в обменной схеме, то есть в стремлении получить требуемый ресурс в обмен за меньшее количество своего ресурса.
Нас будут интересовать механизмы взаимоотношений оператора с потенциальными участниками обменной схемы, которые побуждают их к сообщению достоверной (истинной) оценки обменного коэффициента или, по крайней мере, уменьшают тенденцию завышения оценок. Рассмотрим сначала, с одной стороны, самый простой случай взаимодействия оператора с одним участником обменной схемы, а с другой - самый сложный, поскольку это случай монопольного (единственного) агента, который может диктовать свои условия. Вспомним, что обменные коэффициенты отражают относительную ценность получаемого и отдаваемого ресурсов и представим интересы оператора и агента в виде линейных целевых функций:
(9.1)
(9.2)
jo = Х2 - СХі, Фі = kxi- Х2,
где x1 - количество ресурса, отдаваемое оператором, х2 - количество ресурса, отдаваемое агентом, с - ценность для оператора ресурса агента относительно своего ресурса, k - ценность для агента своего ресурса относительно ресурса оператора.
Примем, что оператору известна величина с, а относительно k он знает только область [a,b] возможных значений. Представим механизм взаимодействия (переговоров) оператора с агентом следующим образом. Агент сообщает оператору оценку se [a,b] коэффициента k. Оператор определяет количество ресурса x1(s), которое он отдает агенту и количество
ресурса x2(s), которое он получает от агента. Зависимости [xi(s), x2(s)] назовем механизмом обмена. Механизм обмена выбирается оператором и сообщается им агенту до начала переговоров. Основное требование к механизму обмена состоит в том, что он должен обеспечивать агенту неотрицательный доход (точнее маргинальную прибыль), в противном случае агент откажется участвовать в обменной схеме.
Примем далее, что ресурс оператора ограничен величиной R, а ресурс агента неограничен.
Задача заключается в том, чтобы определить механизм обмена, который гарантированно обеспечивает оператору максимальный относительный доход. Будем предполагать, что а с. В противном случае, при х = а, складывая ф0 и фь получаем
Фо + Фі = (а - c)xi 0.
Учитывая, что должно быть ф0 0, ф1 0, получаем противоречие, то есть обмен не состоится.
Чтобы определить относительный доход оператора заметим, что максимальный доход оператора при обменном коэффициенте k равен (k - c)R. Действительно, из условия kx1 - x2 0 получаем, что kx1 x2. Поэтому
x2 - сx1 (k - c)x1
и достигает максимума при x1 = R. Гарантированный относительный доход определяется выражением
x2 - cxt (k - c)x1
Q = min
k
(9.3)
Одна из центральных теорем теории активных систем гласит, что в системе центр - активный элемент (центр это оператор, определяющий механизм обмена, а активный элемент это агент, сообщающий оценку обменного коэффициента) всегда существует оптимальный механизм обмена, который является механизмом честной игры [2]. Механизмы честной игры являются неманипулируемыми механизмами, то есть создают 56 заинтересованность у агентов в сообщении достоверной (истинной) оценки обменного коэффициента k. Для того, чтобы определить механизм честной игры, нужно задать в области возможных значений x = (xb x2) некоторое множество X. Это множество оператор сообщает агенту и гарантирует ему, что обмен (xi, x2) будет обеспечивать максимум целевой функции агента на множестве X. Понятно, что поскольку изменить множество X агент не может, то для максимизации своего дохода ему достаточно сообщить истинное значение обменного коэффициента k. Таким образом, задача определения оптимального механизма обмена свелась к определению оптимального множества X. Решим эту задачу, предполагая, что оценки s обменного коэффициента k могут принимать целочисленные значения от a до b. Обозначим ao = a, ai = a + i, i = 1,m, am = b. Идею построения оптимального множества X поясняет рис. 21. Заметим, что максимум целевой функции агента j1 = aix1 - x2 - в т. xi, поскольку угловой коэффициент отрезка прямой [xi-1, xi] равен ai (рис.
21).
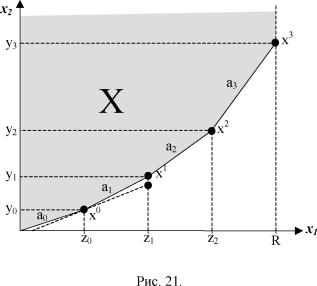
Уі - czi
а гарантированная эффективность
(a - c )r’
(9.4)
m = min m ¦.
0im i
(9.5)
Задача свелась к определению точек излома zi5 i = 1,m -1. Нетрудно показать, что максимум гарантированной эффективности достигается в случае, если все mi будут равны между собой. Из этого факта получаем последовательно:
a0z0 = a1z0 -
z0 =
a0z0 cz0 = Z0 = 1
(a0 - c )R R R
Далее по аналогии
a1Z1 - І1= a2Z2 - І2, z1 = 1 -
a1Z1 I1 CZ1 Z1 I1
(a1 - c )R R (a1 - c)R
В общем случае i m-1
Zi = ^i+1 - ^i,
(9.6)
R (ai - c )R
Для i = m имеем
..= amR -1 m - cR = 1 -/ \ 1
(9.7)
(am - c)R (am - c)R'
Из полученной системы уравнений определяем 1i как функцию m. Обозначим pi = 1 + 1. Последовательно получаем
ai - c
ii = mR,
(9.8)
li = mR[1 + Pi-1 + Pi-1 Pi-2 + ¦¦¦ + pi-1 pi-2- pi], i = 2,m-1.
Из последнего уравнения (9.7) имеем
= (1 -m)R
Pm - 1
Окончательно определяем
m
(9.9)
1 + (Pm - 1)(1 + Pm-1 + Pm-1Pm-2 +¦¦¦ + Pm-1Pm-2 ¦¦¦ P1 ) ’ Пример 11. Пусть m = 1, ао = 4, а1 = 5, с = 3, R = 30. Имеем P1 = 3/2,
1 = 2_
Pm = 3 ;
11 = Rm = 20; z0 = 11 = 20.
Итак, при сообщении оценки a0 = 4 агент получает 20 единиц ресурса от оператора, отдавая взамен 80 единиц своего ресурса. Сообщая a1 = 5, агент получает 30 единиц ресурса от оператора, отдавая взамен 150 - 20 = 130 единиц своего ресурса. Покажем, что манипулируя информацией, агент ничего не выигрывает.
Действительно, если истинный коэффициент обмена равен a1 = 5, а агент занижает оценку и сообщает s = 4, то он получает 20 единиц ресурса в обмен на 80 единиц своего ресурса. Его доход составит
Д1 = 5-20 - 80 = 20,
то есть ровно столько же, сколько он получает, сообщая истинную оценку. Заметим, что применяя простой механизм обмена, ориентированный на минимальное значение обменного коэффициента k = a0 = 4, оператор гарантированно получает доход 4^30 - 3^30 = 30 единиц, независимо от истинного значения обменного коэффициента.
В полученном оптимальном механизме обмена оператор получает меньший доход - 20 единиц, если коэффициент обмена равен а0 = 4 и больший доход - 60 единиц, если a1 = 5. Средний доход для оптимального механизма больше.
Пример 12. Пусть m = 2, ао = 4, а1 = 5, а2 = 6, с = 3, R = 30. Имеем p1 =
3/2, р2 = 4/3,
1 6
1 + )э(і + К) 11
zo = І1 = mR = 6'30/
16,4;
11
І2 = mR(1 + р1) =' зо = 41,
11'2
11
z1 = 12 - 11 =24,6.
В данном случае при минимальной оценке а0 = 4 оператор предлагает к обмену 16,4 единиц ресурса, при средней оценке а1 = 5 - предлагает 24,6 единиц ресурса, а при максимальной - 30 единиц. Гарантированная относительная эффективность по сравнению с предыдущим примером уменьшилась (6/11 2/3), что естественно, поскольку увеличилась
неопределенность информации у оператора. Однако, средний доход составляет около 52 единиц, что существенно выше гарантированного дохода, равного 30 единицам.
Перейдем к исследованию случая нескольких участников обменной схемы. Отметим сразу, что задача поиска оптимального механизма обмена в случае многих участников в настоящее время не решена. Неизвестно даже, существует ли оптимальный механизм честной игры.
Если искать оптимальный механизм на множестве механизмов честной игры, то эту задачу можно свести к задаче линейного программирования большой размерности. Так, даже в случае двух участников, каждый из которых может иметь два значения обменного коэффициента, мы получаем задачу линейного программирования с двадцатью переменными.
К тому же трудно объяснить содержательно оператору (ЛПР), что полученное оптимальное решение действительно является лучшим способом действия и убедить его действовать таким образом. Поэтому задача поиска простых и понятных механизмов обмена, обеспечивающих достаточную эффективность обменной схемы, требует дальнейших исследований.
В заключение рассмотрим кратко механизм выбора обменных схем, когда их несколько. По-прежнему считаем, что количество ресурсов у всех участников, кроме оператора, не ограничено.
Итак, пусть имеются m агентов, каждому из которых нужен ресурс оператора. Таким образом, мы имеем m возможных обменных схем, каждая из которых включает оператора и одного из участников. Обозначим ki -обменный коэффициент i-го агента, ci - доход оператора от единицы ресурса i-го агента. Тогда прибыль оператора на единицу стоимости ресурса, отдаваемого i-му агенту, составит (ciki - 1) = pi.
Пусть p1 p2 - - - pm.
Первое, что приходит в голову в данном случае, это организовать конкурс между агентами на участие в обменной схеме. Естественно, что побеждает агент, предложивший обменный коэффициент si, такой что величина (cisi - 1) максимальна. Из теории конкурсных механизмов известно, что в данном случае побеждает первый агент, сообщая оценку s1, такую что p1 = (c1s1 - 1) близка (немного больше) к p2 = (c2k2 - 1) [2].
Очевидно, что если pi p2, то эффективность такого механизма будет невелика.