Нейронные сети, СИФ и гипернейрон
Заметим, что каждый разряд уточняет адрес:
0,1 ^ 1/2 хо 1 0,10 ^ 1/2 х0 3/4 0,101 ^ 5/8 х0 3/4 - - -
Вспомним теперь, что умножение в двоичной арифметике это просто сдвиг запятой вправо и отбрасывание единицы, с учетом модуля. Таким образом, эволюция нашей системы сводится просто к уточнению адреса начальной точки!
Однако, через 6 итераций последний известный символ уйдет влево, исчерпав всю информацию, которая содержалась в начальных данных! Следовательно, на седьмой итерации мы не сможем сказать, в какую половину интервала I попадет очередная точка траектории.
Понятно, что увеличение начальной точности не изменит ситуацию увеличится лишь число детерминированных шагов. Легко понять причины потери точности: общее решение имеет вид: xn = 2nx0, так что расстояние между сколь угодно близкими начальными точка-
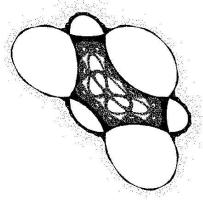
Впервые этот эффект был обнаружен Эдвардом Лоренцем в 1961 году при численном решении простой системы из трех нелинейных уравнений, моделирующих конвекционные потоки в атмосфере. Уравнения были полностью детерминированными, т. е. они не содержали каких-либо случайных величин.
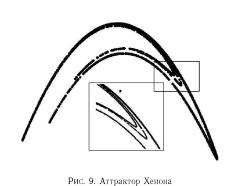
Траектории системы заполняли фрактальное подмножество аттрактор с хаусдорфовой размерностью 2.06. При этом, две численные траектории, стартующие из двух близких начальных точек очень быстро расходились, демонстрируя совершенно различное поведение. Поскольку начальные данные для метеосистем всегда получаются с конечной точностью, Лоренцу стало ясно что прогноз погоды будет всегда ограничен тем диапазоном времени, на котором расхождение близких траекторий еще не превышает некоторой заданной величины.
Такой временной масштаб его называют горизонтом прогноза, по-видимому, не превышает недели(4). Существенно, что ограниченная предсказуемость является следствием нелинейности уравнений. В более общем случае оказалось, что динамический сценарий, которому следуют траектории хаотических систем определяется типом нелинейности, и почти не зависит от вида самого уравнения!
Однако, обсуждение этих вопросов выходит за рамки данной лекции. В заключение еще раз заметим, что странные аттракторы хаотических динамических систем по своей сути являются синонимами предельных образов (аттракторов или фракталов) СИФ.
Фракталы в геометрии результат работы системы линейных сжимающих отображений (СИФ); в динамике, сжатие определяется нелинейными диссипативными уравнениями.
Примечания
1. В физике под динамической системой понимают обычно систему (автономных) обыкновенных дифференциальных уравнений х' = f (х), х G Rn, где х' = dx/dt, и f : U ^ Rn определено для некоторого открытого подмножества U G Rn. Пространство Rn называют фазовым пространством, а f (х) векторным полем, так как ре-
шение уравнения есть кривая с касательным вектором x'. В более общем случае под динамической системой в фазовом пространстве M понимают однопараметрическую группу преобразований gt : M ^ M, где параметром обычно служит время: непрерывное (t € R) или дискретное (t € Z). Точка x0 ? M под действием gt переходит в точку xt = gt(x0), при этом групповое свойство означает, что gtgs = gt+s.
Последовательность точек {xt} образует орбиту группы. Если M дифференцируемое многообразие, и gt взаимно однозначное дифференцируемое отображение, такое, что обратное к нему g-t обладает аналогичными свойствами (такое отображение называют диффеоморфизмом), то пару (M, {gt}) называют фазовым потоком или же каскадом для случая, когда время дискретно.
Легко показать, что физическое определение сводится к абстрактному. Рассмотрим динамическую систему заданную уравнением ж' = ах, х ? R. Его решение можно записать в виде xt = gtx0 = eatx0, так что поток индуцируется действием непрерывной группы gt = eat однопараметрических преобразований в R.
о возвращении. Пусть B ? X, р измеримо, X компакт и обратимое преобразование f сохраняет меру на X : p{f (B)} = p{B}. Тогда существует некоторое n (возможно, зависящее от x0), такое, что почти все точки x0 ? B возвращаются в B, т. е. f on(x0) ? B. Иными словами, орбита любой точки p ? B : {p, f (p), f (p)...} содержит некоторые образы f k (p), которые вновь попадают в B. Предположим, что это неверно и часть точек, образующих подмножество A с B, никогда не возвращаются.
Тогда множества {A,f(A),f(A),...} никогда не пересекаются! Действительно, пусть точка P ? f (A) П f o3(A). Очевидно, что f-1 (P) ? A, но она же принадлежит и f (A), так как P ? f o3(A). Но это невозможно, поскольку A не содержит возвращающихся точек.
Следовательно, орбита f crrcn(A) разбивает X на бесконечную последовательность непересекающихся фрагментов, которые могут иметь только нулевую меру: X-компакт и его мера конечна.
3. Динамическая система (X, д) называется хаотической, если выполняется следующие условия:
- пусть x ? X и U открытое подмножество, содержащее X. Если для некоторого 5 0 существует такое n и такая точка y ? U, что d(gn(x),gn(y)) 5, то д обладает существенной зависимостью от начальных условий;
- g транзитивно, т. е. для любой пары открытых множеств U, V существует такое n, что gn(U) П gn(V) = 0;
- периодические точки g плотны в X, т. е. в любой окрестности любой точки в X существует по крайней мере одна периодическая точка (и, следовательно, бесконечно много периодических точек).
4. Любопытно, что за 175 лет до Лоренца, ученик Эйлера, академик С. Я. Румовский писал в статье Рассуждения о предсказании погод: Что же думать о предсказаниях погоды на целый год? Они не что иное суть, как тщетное и пустое умствование, которым легкомысленным людям во многих случаях вред нанести может.
Статья была опубликована в 1 Докладов Академии наук за 1786 год. Они назывались тогда Новые ежемесячные сочинения к пользе и увеселению служащие.
Путеводитель по литературе. Связь фракталов и хаотических систем великолепно описана в книге Кроновера [23]. На сайтах [24] можно найти хорошие примеры дискретных преобразований на плоскости. Доступное изложение основ теории нелинейных динамических систем содержится в монографиях [25,26] и журнальных обзорах [27,28].
Строгому обсуждение концепции аттрактора посвящена статья Милнора [29]. Хорошие вводные курсы по топологической динамики можно найти на сайтах [30,31], а современное изложение эргодической теории динамических систем на Web-страничке [31].
Нейронные сети, СИФ и гипернейрон
Что это? Никак игрушка!
Подберите фалды! ...
Смотрите издали! ...
Козьма Прутков
Как известно, основной элемент модели нейронной сети формальный нейрон вычисляет скалярное произведение входного вектора
x = (xo,xi,... ,xn)T
и вектора синаптических весов
w = (^0,^1, - - - i^n)T,
которое преобразуется затем функцией активации g, вычисляющей выход нейрона у:
y(x, w) = g(x ¦ w)
В качестве g обычно используется либо функция Хевисайда (ступенчатая), либо сигмоида.
Пусть гиперболическая СИФ задана системой {(X, d); f1,f2 ,- - - ,fq }. Пусть Af аттрактор СИФ. Существует два способа приближенного построения этого фрактала.
Первый из них начинается с выбора одной или нескольких начальных точек х0 и вычисления их дискретных орбит длиной N. Пусть, как и раньше, а = (а1, - - - , aN); an G {1, - - - , q}. Тогда
при достаточно большом N множество:
A(x0, N) = U f*N ¦¦¦ f 1 (xo)
а
является хорошим приближением Ар. Этот способ можно оптимизировать, если выбрать в качестве х0 неподвижную точку одного из fk так, что х0 е Ар.
Заметим, что вычисление N орбит на один шаг вперед не эквивалентно вычислению одной орбиты на N шагов. Другой способ заключается в определении траектории начального компактного множества Ао е H(X,d):
N
An+1 = F(An) = ^ fi(An); n = 0,..., те.
i
Последовательность An сходится к AP в метрике Хаусдорфа, так что при достаточно больших N, FoN(A0) AP. Рис. 10 иллюстрирует этот подход.
Коллаж состоит из трех начальных множеств, которые эволюционируют под действием F и приводят к аппроксимации фрактала, показанной на рис. 11.
Предположим, что мы собираемся построить на экране компьютера аттрактор СИФ. Будем считать, что экран состоит из квадратных пикселов и горизонтальное и вертикальное разрешения равны.
Пусть X = Su С R2, Su единичный квадрат с разбиением, соответствующим выбранному разрешению. Чтобы упростить обозначения, мы будем использовать значок s вместо координат пиксела xij. Снабдим каждое An индикаторной функцией (нейроном) y : Su ^ {0,1} такой, что для каждого пиксела s G Su:
(п) = I
1 , s G An 0 , s G An
Определим веса
( 1 , если fi(s') = s для некоторого i 0 , в противном случае
и зададим динамику ys(n) как
ys(n + 1) = g( 53 wss'ys'(n))
s'es
где g ступенчатая функция.
Очевидно, что по виду и смыслу полученное выражение определяет бинарную нейронную сеть с |S"| нейронами ys и синаптическими весами wss/, которая реализует СИФ. Заметим, что каждый нейрон такой сети имеет только бинарные веса и максимальное количество нейронов, с которыми он связан, равно q. Несмотря на то, что число весов может быть очень большим, подавляющее большинство из них будут нулями.
Так что результирующая сеть будет пространственно разреженной.
Детерминированная СИФ и эквивалентная ей нейронная сеть позволяют получать лишь черно-белые изображения аттракторов. Для генерации полутонов следует использовать ССИФ.
Поскольку принципы построения соответствующей нейросети остаются прежними, мы опускаем здесь этот вариант.
Дальнейшее обобщение этих результатов приводит к рассмотрению случайной итеративной нейронной сети, которая в определенном смысле эквивалентна дискретной динамической системе. Представим себе формальный нейрон, который устроен следующим образом. На каждый его вход подается вектор u € Rm.
Весами служат множество W векторов wj € Rk, функцией активации Ta,W является ССИФ, а выходом вектор у € Rm, так что y = TffjW(ui, u2,..., uk), где множество а нумерует выбор отображений, входящих в T с соответствующими вероятностями, так же как и в разделе Фракталы и системы итеративных функций (см. с. 139-144). Такое устройство называют вероятностным гипернейроном.
Случайная итеративная нейронная сеть (СИНС) состоит из трех гипернейронов и имеет архитектуру обычной рекуррентной нейронной сети, которая реализует аттрактор ССИФ. Динамику СИНС можно описать парой (X,Af), где X пространство состояний СИНС и Af ее глобальный аттрактор. Пусть (Y,Ag) дискретная динамическая система с аттрактором Ag.
В начале 2000 года Фернандо Ниньо (The University of Memphis) показал в своей диссертации, что для любой заданной пары (Y,Ag) существует (X, Af) такая, что хаусдорфо-во расстояние h(Af ,Ag) между аттракторами динамической системы и СИНС можно сделать сколь угодно малым. Иными словами, СИНС является аппроксиматором дискретной динамической системы с заданным аттрактором! Необходимый для аппроксимации набор ССИФ можно най-
ти генетическим алгоритмом. К сожалению, подробное обсуждение этой интересной проблемы выходит за рамки лекции.
Путеводитель по литературе. Автору известны всего три работы [3739], специально посвященные связи СИФ и нейронных сетей.
Описание гипернейрона можно найти в диссертации Ф.Ниньо [40].
Глоссарий
Запятирующее тире отражает кумулятивное диффундирование смыслокачества в новизну подтекстовых проводок в ситуации резкого спада количества определяющих указателей.
Павел Таранов Маневры общения
Этот раздел содержит предварительные сведения, т. е. определения и понятия, чуть более содержательные, чем просто определения. Они собраны из разных областей математики с целью сделать чтение Лекций по возможности независимым от сопутствующей литературы. Мы будем использовать ниже следующую символику:
- Запись x G X означает, что элемент x принадлежит множеству X.
- Запись V x читается: для любых x (для всех x), запись 3 у существует у, а запись Vx 3 у | означает: для любого x существует у, такой что...
- Запись X = {x|A} обозначает множество таких элементов x, для которых справедливо условие A.
- Запись A с B (A С B) означает, что A содержится в B (содержится в B или совпадает с ним, соответственно).
- Наконец, A ^ B читается: A влечет B.
Множество возникает благодаря объединению отдельных вещей в одно целое. Для того, чтобы избежать парадоксов, полагают, что элементы a,b,c,... особым не подлежащим определению образом порождают множество X. Иными словами X задано, если известно, входит туда элемент или нет(1).
Природа самих элементов безразлична: ими могут быть, например, Луна и прошлогодний снег.
Объединением множеств A и B называют множество C = A U B, состоящее из элементов c G C, каждый из которых принадлежит A или (и) B.
Пересечением A и B называют множество C = A П B, каждый элемент которого c входит ив A, и в B. Эти определения легко обобщаются. Для произвольного множества индексов I = {i} каждому i поставим в соответствие множество Aj. Тогда объединение
C = UAj = {c G C|3i G I ^ c G Aj}.
Аналогично определяется пересечение:
C = nAi = {c G C|Vi G I ^ c G Aj}.
Пустое множество обозначается 0.
Семейство множеств A = {Aj} называют покрытием множества B, если B С U{Aj|Aj G A}, т. е. каждая точка B принадлежит некоторому элементу A. Частный случай покрытия, когда AjnAj = 0, Vi,j называют разбиением B.
Два множества A и B можно поставить во взаимно однозначное соответствие, если Va G A 3b G B и наоборот. Так определяется отношение эквивалентности A = B; говорят еще, что A и B имеют одинаковую мощность.
Если A = {1,2,...} то A называют счетно-бесконечным.
Для описания мощности множества служат кардинальные числа. Если множество конечно, это просто число элементов в нем.
В случае бесконечного множества A, кардинальное число определяют присвоением имен кардинальным числам конкретных множеств, с которыми можно сравнить A. Кардинальное число счетно-бесконечного множества обозначают символом алеф-нуль Н0. Примером несчетного множества являются вещественные числа интервала [0,1].
Его кардинальное число |c| называют мощностью континуума. Ясно, что мощность всей вещественной оси тоже | c|; в этом легко убедиться с помощью преобразования:
x ^ 1/2(1 + th x). Кантор показал, что точки квадрата и точки отрезка эквивалентны, т. е. мощность R равна |c|.
Соответствие между различными множествами удобно описывать функциями или отображениями: f (*) или f : A ^ Y. Если A ? X, то и f [A] = {f (x)|x ? A}. Аналогично, если B ? Y, то f1 [B] = {x|f (x) ? B} подмножество в X. Подмножество {f (x)} ? Y это область значений функции, а {x} ? X ее область определения. Функциональные отношения между множествами имеют определенную классификацию:
- Если образ всего множества A совпадает с B или, что тоже самое, каждый элемент из B является образом по крайней мере одного элемента из A, то говорят, что f сюръекция или отображение на.
- Функцию f : A ^ B называют инъективной или взаимно-однозначной если для Vy ? B существует не более одного элемента x ? A такого, что у = f (x). Очевидно, что в этом случае f (x) = f (У) ^ x = у.
- Биективное отображение или биекция это функция, которая является одновременно сюръективной и инъективной.
Если A и B совпадают, то f : A ^ A и элемент x, удовлетворяющий условию x = f (x), называется неподвижной точкой отображения f. Например, каждое непрерывное отображение f : [a, b] ^ [а, b] отрезка в себя имеет хотя бы одну неподвижную точку(2).
Абстрактное множество называют группой, если:
ных преобразований. С другой стороны, в арифметическом пространстве Xn точка x определяется абсолютно набором n чисел (x1,... , xn) с точностью до тождественных преобразований.
Аффинная геометрия удовлетворяет более скромному требованию det A =0. Можно задать группу в общем виде: x* = f (x, у); y* = g(x, y), где f и g нелинейные CN-функции, т. е. функции, обладающие непрерывными производными до N-го порядка. Если такими же свойствами обладают обратные преобразования (а их существование гарантирует группа), то мы получим геометрию гладких многообразий.
Такое многообразие определяет объект с точностью до произвольных гладких деформаций. Вырожденный случай C0 это уже топология.
Метрическое пространство (M, d) это множество M вместе с вещественнозначной функцией d, определенной на декартовом произведении M х M, называемой метрикой на M и удовлетворяющей следующим требованиям:
- d(x, у) ^ 0; d(x, у) = 0 ^ x = у
- d(x, у) = d(y,x)
- d(x, z) S d(x, y) + d(y, z)
Для M = Rn обычная евклидова метрика:
1 1/2
d(x,y) = [53(xi - уі)
легко обобщается до Lp метрики Минковского:
dP(x,y) = \^2(xi - Уі)Р
Располагая метрикой, нетрудно ввести понятие сходимости по аналогии с тем, что было в Xn. Говорят, что последовательность точек {xn}, n = 1,2,..., метрического пространства (M, d) сходится к x G M, если d(x,xn) ^ 0, при n ^ ж. Различные метрики порождают разные сходимости.
Метрика di эквивалентна d2 в M, если существуют две постоянные 0 ci c2 те такие, что:
cidi(x,y) d2(x,y) c2di(x,y), V(x,y) G M x M
Последовательность {xn} G (M, d) называют последовательностью Коши, если Ve 0 3N | n, m N ^ d(xn,xm) e. Заметим, что эта последовательность не обязательно сходится к определенному пределу. Пусть (M,d) метрическое пространство и {xn} последовательность Коши, сходящаяся к точке x G M. Пусть также f : M ^ M непрерывная функция. Тогда:
lim f(xn) = f(x).
n ^
Пространство (M, d), в котором любая последовательность Коши сходится, называется полным.
Пусть (M, d) метрическое пространство и r 0 действительное число. Тогда открытым шаром в точке a G M называется подмножество B(a,r) С M : B(a,r) = {x G M | d(a,r) r}. Шар называется
замкнутым, если d(a, r) ^ r.
Открытым множеством в (M, d) называется подмножество A С M, для любой точки x G A которого существует такое r 0, B(x,r) С A. Пустое множество 0 и само пространство M открыты.
Замкнутым множеством в М называют дополнение открытого множества; 0 и M объявляются замкнутыми. Метрическое пространство M называют компактным, если оно удовлетворяет аксиоме Лебега-Боре-ля: из любого покрытия M открытыми множествами можно выделить конечное подпокрытие.
(M, d) называют вполне ограниченным, если V e 0 существует конечное покрытие пространства M шарами диаметром e.
Понятия компактности и ограниченности заменяют понятие конечности в чистой теории множеств. Компактным (вполне ограниченным) множеством в (M, d) называют такое подмножество A С M, для которого подпространство A компактно (вполне ограничено).
Наконец, для (M, d) следующие три условия эквивалентны: М компактно, или любая бесконечная последовательность в М имеет по крайней мере одну предельную точку, или М полное и вполне ограниченное.
Пусть H(M) пространство, точками которого являются компактные множества из (M, d). Пусть A,B G H. Определим метрику h в H как
h(A,B) =max{maxmin d(x,y), max min d(x,y)}
x^A y?B y^A x?B
Bеличина h(A, B) называется расстоянием Хаусдорфа и удовлетворяет всем аксиомам метрики. Можно показать, что (H(M),h) является полным метрическим пространством.
В тексте Лекции дано эквивалентное определение этой метрики.
Пусть (M,d) метрическое пространство и s 0. Отображение f : M М называют подобием с масштабным коэффициентом s, если d(f (x),f (y)) = sd(x,y), Vx,y G M и сжимающим отображением с коэффициентом сжатия s, если существует такое число 0 ^ s 1, что d(f (x),f(y)) sd(x,y), Vx,y G M. Иными словами, f сжатие, если расстояние между образами двух произвольных точек в s раз меньше исходного. Определим для f множество итераций вперед f n : M M, n = 1,2,... соотношениями:
fo0(x) = x; fo1 (x)
f (x); fon+1(x) = f * fon(x) = f (fon(x)).
Если f обратима, аналогично определяются итерации назад:
f-on(x) = (f on)-1 (x).
Пусть f : M M сжатие в полном метрическом пространстве (M, d). Тогда справедлива Теорема о сжимающем отображении: f имеет единственную^3) неподвижную точку f (x) = xf G M и Vy G M последовательность fon(y) сходится к
xf : lim fon(y) = xf.
n ^O
Множество B c M называют плотным в M, если любое x G M является пределом последовательности элементов из B.
Пусть X множество точек x. Систему B подмножеств X называют
ст-алгеброй, если
1. 0, X G B
2. A G B ^ X - A G B
3. An е B, n = 1,2,... ^ U An е B, f| An е B
Наименьшая из ст-алгебр в метрическом пространстве Rn называется
борелевой ст-алгеброй.
Пара (X, B) называется измеримым пространством. Пусть (X, B) измеримое пространство. Вещественная функция = (A), A е B, принимающая значения из интервала [0, те], называется мерой, если
- (0) = 0
- (A) ^ 0, VA е B
- если (An}]]=1 непересекающиеся множества из B, то
ми r=i An) = E ~=i ^
Тройка (X, B,) называется пространством с мерой. Например, лебегова мера на вещественной оси это просто длина интервала вида (a,b), [a,b), (a,b], [a,b]. Мера Лебега не является универсальной: существуют множества, не являющиеся -измеримыми.
Тем не менее, -мера является эталоном не только во многих разделах математики, но и в эргодической теории гладких динамических систем.
Множество S имеет меру нуль, если оно может быть покрыто системой интервалов, сумма длин которых произвольно мала. Иными словами, такое S можно вложить в борелево множество B мерой меньшей чем е, Ve 0. Если S можно получить из борелева множества B добавлением или выбрасыванием множества точек нулевой меры, то (S) = (B). Такие множества называют -измеримыми.
Выражение почти для всех х понимают в смысле для всех х, за исключением множества меры нуль.
Если (X) = 1, называют вероятностной мерой, а (X, B,) вероятностным пространством.
Пусть (X,B,) вероятностное пространство. Преобразование T : X ^ X называется измеримым, если для любого A е B, T-1A = {х : Tx е A} е B.
Говорят, что измеримое преобразование T сохраняет меру , если для каждого A е B, (T-1A) = (A). Меру называют в этом случае
T-инвариантной.
Четверка (X, B,, T), где T преобразование, сохраняющее меру, называется динамической системой.
Примечания
1. При этом абсолютно неясен способ, посредством которого мы могли бы выяснить, входит элемент а в A или нет. Например, если A задано запахом, а B вкусом, можем ли мы решить эквивалентны они или нет?
Приведем пример одного парадокса Рассела. Пусть A множество всех натуральных чисел. Предположим, что каждое из этих чисел можно определить фразой, содержащей менее 20 русских слов. Содержит ли A весь натуральный ряд?
Считая, что русский язык содержит не более чем n слов и, следовательно, не более чем n20 нужных нам фраз, можно полагать, что A конечно. Но тогда определим наименьшее натуральное число, не входящее в множество A. Это число по определению не входит в A, но должно входить в него, поскольку определяется фразой, не превышающей 20 слов.
Очевидно, A содержит весь натуральный ряд, а парадокс возникает потому, что мы дополнили русский язык фразой, выделенной курсивом.
2. Определим новую функцию: g(x) = f (x) x для каждой x G [a, b]. Она непрерывна и g(a) 0, g(b) 0, если концы интервала не являются неподвижными точками. Но если непрерывная функция меняет знак, найдется хотя бы одна точка x в которой g(x) =0 ^ f(x) = x.
3. Действительно, пусть f (x) имеет две неподвижных точки: x*,y*.Тогда, d(f(x*),f(y*)) sd(x*,y*). Но тогда d(f(x*),f(y*)) = d(x*,y*) ^ sd(x*,y*). Следовательно, d(x*,y*) = 0.
Путеводитель по литературе. Основные понятия теории множеств можно найти в [33-35]. Небольшая книжка [41] содержит простое введение в теорию меры, история развития которой изложено в работе Лебега [3]. Отличное введение в теорию гладких многообразий содержит учебник [5].
Метрика Хаусдорфа в пространстве компактов и ее связь с фракталами описана в [2]. Сводку многих приведенных определений можно найти в справочнике [36].
Summa sine laude16
Разумеется, все что написано выше можно было бы изложить гораздо
лучше, но ведь можно было и хуже...
Литература
1. Пуанкаре А. О науке. - М.: Наука, 1983. - 560 с.
2. Barnsly MFractals everywhere. - Academic Press, 1988. - 394 pp.
3. Лебег А. Об измерении величин. - М.: ГУПИМП, 1960. - 204 с.
4. Стинрод Н., Чинн У. Первые понятия топологии. - М.: Мир, 1967. - 224 с.
5. Chillingworth D. Differential topology with a view to applications. - Pitman Press, 1976.-291 pp.
6. Горелик Г.Е. Размерность пространства. - М.: Изд-во МГУ, 1983. - 216 с.
7. Зельдович Я. Б., Соколов Д.Д. Фракталы, подобие, промежуточная асимптотика // УФН. - 1985. - т. 146. - с. 493-506.
8. Perdang J.Astrophysical fractals: An overview and prospects // Vistas in Astronomy. - 1990. - v. 33. - pp. 249-294.
9. Соколов И. МРазмерности и другие геометрические критические показатели в теории протекания // УФН. - 1986. - v. 150. - pp. 221-253.
10. Голдман С. Теория информации. - М.: Мир, 1967.
11. Реньи А. Трилогия о математике. - М.: Мир, 1980. - 376 с.
12. Федер Е. Фракталы. - М.: Мир, 1991. - 260 с.
13. Баренблатт Г. И. Подобие, автомодельность, промежуточная асимптотика. -Л.: Гидрометеоиздат, 1982. - 255 с.
14. Мандельброт Б. Общие свойства фракталов // В сб.: Фракталы в физике. -М.: Мир, 1988.-с.9-47.
15. Mandelbrot B. Self-affine fractals and fractal dimension // Physica Scripta. - 1985. - v. 32. - pp.
257-260.
16. Рихтмайер Р. Принципы современной математической физики. т. 2. - М.: Мир, 1982. - 486 с.
17. Иванов Л. Д. Вариации множеств и функций. - М.: Наука, 1975.
18. Янг Л. Лекции по вариационному исчислению и теории оптимального управления. - М.: Мир, 1974. - 488 с.
19. Pfeifer P, Obert MFractals: Basic concepts and terminology // Chapter 1.2 in: Fractal Approach to Heterogeneous Chemistry: Surfaces, Colloids, Polymers / Ed.: David Avnir. - John Wiley Sons Ltd., Chichester. - 1989. - p. 11.-40.
20. Godreche C., Luck J.M.Multifractal analysis in reciprocal space and the nature of the Fourier transform of self-similar structures // J. Physics. A.: Math. Gen. -1990. - v. 23. -pp.
3769-3797.
21. Hatchinson J. Fractals and self-similarity // Indiana Univ.
J. Math. - 1981. - v. 30. -pp. 713-747.
22. Hatchinson J. Fractals: A mathematical framework. - Department of Mathematics, School of Mathematical Sciences, Australian National University, Dec.
1996. URL:
23. Кроновер Р. МФракгалы и хаос в динамических системах. - М.: Постмаркет, 2000. - 350 с.
24. Bourke P An introduction to fractals. - May 1991.
25. Малинецкий Г. Г., Потапов А. Б. Современные проблемы нелинейной динамики. - М.: Эдиториал, 2000. - 335 с.
26. Лоскутов А. Ю., Михайлов А. С. Введение в синергетику. - М.: Наука, 1990. - 272 с.
27. Eckmann J.P., Ruelle D. Ergodic theory of chaos and strange attractors // Rev.
Mod. Phys. - 1985. - v. 57. - pp.
617-656.
28. Schaw R. Strange attractors, chaotic behavior, and information flow // Z. Naturforsch. - 1981. - v.36a. -pp.80-112.
29. Milnor J. On the concept of attractor // Commun.
Math. Phys. - 1985. - v. 99. -pp.177-195.
30. SprottJ.
Strange attractors: Creating patterns in chaos. - New York: M T Books, 1993. - 591 pp.
33. Александров П. С. Введение в теорию множеств и общую топологию. - М.: Наука, 1977. - 368 с.
34. Келли Дж. Л. Общая топология. - М.: Наука, 1968. - 432 с.
35. Колмогоров А. Н., Фомин С. В Элементы теории функций и функционального анализа. - М.: Наука, 1989. - 496 с.
36. ФорР., Кофман А., Дени-ПапенМСовременная математика. - М.: Мир, 1966. -271 с.
37. Severyanov V.M. Automata network dynamical systems for construction of fractal objects // Electronic Proceedings of IMACS ACA’98 the 4th International IMACS Conference on Applications of Computer Algebra.
Czech Technical University, Prague, Czech Republic, August 9-11, 1998. - 8 pp. URL:
38. Stark J. Iterated function systems as neural networks // Neural Networks. - 1991. - v. 4. - pp.
679-690.
39. Bressloff P. C., Stark J. Neural networks, learning automata and iterated function systems // In: Fractals and Chaos / Eds.: A. J. Crilly et al. - 1991. - Springer-Verlag. -pp.
145-164.
40. Nino F. Random iterated neural networks: Properties, evolutionary design and applications. - Doctoral Dissertation, University of Memphis, May 2000. - 103 pp. URL: