Фракталы, неполная автомодельность и контекстно-свободные грамматики
Она является непрерывной возрастающей функцией, которая тем не менее почти всюду имеет нулевую производную (т. е. горизонтальна!). Ее называют чертовой лестницей (рис.
3).
Пример 2. Кривая Коха. Возьмем равносторонний треугольник и определим следующую элементарную операцию: каждая сторона делится на r = 3 части, после чего средний сегмент заменяется на равносторонний треугольник.
Операция повторяется n раз. То, что получится при n ^ те, и есть триада (снежинка) Коха (рис. 4)
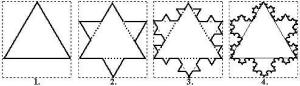
Ясно, что это множество самоподобно, точно так же, как и сам процесс его построения. На любом шаге его линейный элемент длины l заменяется на N = 4 элемента длиной lr-1 = 1/3 каждый.
Поэтому размерность подобия или емкость dc = lnN/lnr = ln4/ ln3 1,2619. Триада ^ха является математической моделью кривой побережья, с которой работал Ричардсон.
Любопытно, что в R2 можно построить множества с дробной размерностью, которые обладают инфернальным свойством призраков или вурдалаков: они не отбрасывают тени. Точнее, для таких объектов лебегова мера проекций на некоторые (или даже на все) направления равна нулю.
Примечания
1. Наиболее важным обстоятельством здесь является переход к пределу даже для гладкой кривой. Действительно, сегмент дуги рассматриваемый непосредственно, ничем не отличается от его половины удвоенной микроскопом.
Целое однородно с частью и как заметил Пуанкаре [1]: Здесь заключается противоречие, или скорее это было бы противоречием, если бы число членов предполагалось конечным; в самом деле, ясно, что часть, которая содержит менее членов сравнительно с целым, не может быть подобной целому.
2. Напомним, что множество X на R имеет меру нуль, если его можно покрыть интервалами, сумма длин которых произвольно мала. Например, X состоит из рациональных чисел из (0,1). Они могут быть записаны в виде последовательности: а1, а2, а3,..., например так:
1/2, 1/3, 2/3, 3/4, 1/5, 2/5,...
Для любого е 0, аі можно заключить в интервал длины е/2; а2 в интервал длины е/4;... ап в интервал длины е/2п. Эти интервалы покрывают X и сумма их длин равна е. Следовательно, множество рациональных чисел имеет меру нуль.
3. Действительно, любому набору {а1,..., ап,... | а^ = 0 или 2} можно поставить в соответствие последовательность b1,..., bn,..., где bn = 0, если ап = 0 и bn = 1, если ап = 2. Но такая последовательность просто двоичный код числа, принадлежащего [0,1].
Путеводитель по литературе. Лучшими, по моему мнению, являются обзоры [7,9] написанные для физиков. Работы Ричардсона изложены в монографии [12], а в [13] им посвящена целая глава. Статьи Мандельброта в [14,15] весьма содержательны, но не подходят для первого чтения.
Небольшая книга Лебега [3] содержит обсуждение упомянутых парадоксов. Описание функции Кантора можно найти в [16], а примеры фракталов-вурдалаков приведены в дополнении к книге [17].
Наконец, некоторые вопросы, связанные с тонкой сходимостью, строго рассмотрены в [18].
Фракталы, неполная автомодельность и контекстно-свободные грамматики
Plus ca change, plus c’est la meme chose.
Чем больше оно изменяется, тем более остается тем же.
Французская пословица
Вернемся к построению триады Коха. Здесь все легко считается. Обозначим через L ребро треугольника на первом шаге. На n-ом шаге размер одной стороны b = L/3n, а периметр Lb = 3L(4/3)n (рис.
4).
Когда n ^ те, b ^ 0, Lb ^ те. Поскольку n = lg(L/b)/ lg 3, имеем:
Lb = 3Ll0a lg(L/b) = 3 L(L/b)a,
где a = (lg4 - lg 3)/ lg 3 0, 2618.
Мы легко получим формулу Ричардсона, если положим:
А = L1-a = Ld ; Lb = 3Аb1-D; D = 1 + a = 1,2619.
Аналогия с береговой линией становится полной, поскольку число звеньев триады N = Lb/b = Аb-D и суммарная площадь квадратов, построенных на периметре, Nb2 = Аb2-D ^ 0 при b ^ 0 (D 2). Мы можем получить конечную величину, если удастся найти такое D*, что NbD* = А, где 1 D* 2; при этом Nb = те и Nb2 = 0, когда b ^ 0. Легко усмотреть основные особенности построения триады:
1. Однородность: каждая сторона треугольника n-го шага порождает одинаковое число звеньев n + 1.
2. Самоподобие: число звеньев n +1 шага зависит только от отношения звеньев n-го и n +1 шагов.
Оказывается, что этих двух условий, заданных локально, достаточно для получения формулы Ричардсона(1\
Рассмотрим произвольную кривую, которая аппроксимируется системой ломаных линий с уменьшающейся длиной звена. Пусть малая
окрестность кривой содержит две соседних вершины ломаной с длиной звена а. Пусть Nab число вершин ломаной со звеном b а, расположенных между теми же вершинами. Свойство локального самоподобия означает, что Nab асимптотически при а/b ^ те можно представить разложением, главный член которого не зависит от а и b, а является функцией их отношения: Nab = f (а/b) при фиксированном а/b ^ 1. Возьмем новую ломаную с длиной звена c ^ b. В силу локальной однородности и самоподобия число ее звеньев, приходящихся на длину а, равно f(а/c). С другой стороны, это же число равно произведению (Nab) х (Nbc).
Здесь первый сомножитель число b-звеньев внутри одного а-звена, а второй число c-звеньев внутри одного b-звена. Таким образом, получаем функциональное уравнение:
f (а/c) = f (а/^f (b/c).
Замена переменных а/b = x; а/c = у дает:
f (y)/f (x) = f (y/x).
Дифференцируя обе части по у и полагая у = х, получим: f' (x)/f (x) = (1/x)f '(1) = D/x или f (x) = xD.
Следовательно, при упомянутых предположениях для длины ломаной справедлива асимптотика:
Lb = aD b1 D + ...
Напомним, что процедура называется автомодельной, если ее характеристики на двух смежных уровнях связаны друг с другом преобразованием подобия. Асимптотика показывает, что фракталы обладают свойством неполной автомодельности.
Поясним этот момент. В общем случае длина аппроксимирующей ломаной для непрерывной кривой между двумя точками, разделенными расстоянием а, зависит от а и длины звена b. Из соображений размерности La = af (а/b).
Для гладкой кривой при а/b ^ те (b ^ 0) функция f стремится к конечному пределу f(те). Именно тогда величина f (те)а является длиной отрезка гладкой кривой. Например, для окружности с диаметром а, f (те) = п/2.
Таким образом, длина окружности автомодельна по параметру а/b при а/b ^ те. Для фрактальных кривых конечного предела f (а/b) не существует. Однако
имеет место неполная автомодельность:
f (a/b) (a/b)D-1.
Разумеется, D зависит от геометрии кривой и не определяется из соображений размерности.
Существует любопытный подход к неполной автомодельности, связанный с символической динамикой. Рассмотрим бинарное слово (двоичную последовательность):
z = Z0Z1 . ..zr-1,
где zj нули, либо единицы. Длина слова log2 z = r, а s ^ r число мест, занятых единицей. Определим гомоморфизм T : [0,1] ^ [0,1] уравнениями: T(0) = 0r, T(1) = z. Пусть, например, z = 101.
Возьмем точку x0 = 1 и рассмотрим последовательность итераций: ж1 = T(x0),... ,xk = T(xk-1). В результате получим последовательность:
жо = 1
x1 = T(1) = 101
ж2 = T(T(1)) = T(101) = T(1)T(0)T(1) = 101000101
Можно убедиться, что неподвижной точкой xy гомоморфизма T будет предел limk^^ xk, удовлетворяющий уравнению T(x) = ж:
xf = 10100010100000000010100010100...
Это символическая запись множества Кантора. Действительно, 101 представляет собой код первого шага построения этого фрактала, когда мы удаляем середину (0) единичного интервала.
На втором шаге та же процедура применяется к получившимся подинтервалам: [0,1/3] ^ 101; [2/3,1] ^ 101 ит.д.
Примечания
1. Или на другом языке получения ренормгруппы, относительно которой самоподобные системы являются инвариантными множествами. Канторову пыль K можно рассматривать как подмножества интервала [0,1]. Пусть преобразование S множества F на вещественной оси дает образ S(F) и обладает следующим свойством:
образ объединения двух множеств равен объединению их образов. Рассмотрим два отображения:
Si(F) = [ж/3: ж е F]
S2(F) = [(ж + 2)/3: ж е F]
S1 отображает канторово множество в его левую половину, а S2 в правую. Очевидно, T(F) = SiU S2 оставляет пыль неизменной. Преобразования, оставляющие множество неизменным, T(K) = K называются симметриями K. Если приложить T к интервалу [0,1] несколько раз, то Tn([0,1]) = K. Фактически K можно
генерировать из любого ограниченного множества вещественной оси, даже из любой единственной точки ж0 : T(xo) тогда состоит из двух точек, T2 (ж0) из четырех и т. д. На языке теории ренорм-групп K единственная притягивающая точка или инвариантное множество Т. В этом контексте dc = ln 2/ ln 3 результат того, что Т объединение двух сжатий. Можно показать, что Т,Т2,... единственные симметрии канторова множества.
Путеводитель по литературе. Монография [13]единственный известный мне источник, где фракталы изложены с позиций неполной автомодельности.
Связь свойств самоподобия и однородности с теорией групп обсуждается в обзоре [19]. Связям фракталов с теорией чисел и символической динамикой посвящены работы [2,20,23].
Фракталы и системы итеративных функций
Но как же оно образуется, если не содержится в том же своем прообразе?
Николай Кузанский Игра в шар
Отображение f : X ^ X, действующее в метрическом пространстве (X, d), называется сжимающим, если существует s е [0,1) такое, что
d(f(ж)^Ы)
для всех х и у из X; s называется коэффициентом сжатия отображения.
Системой итеративных функций (СИФ) (X,{/*}), i = 1,2 называют набор сжимающих отображений5 {/*}, в компактном метрическом пространстве (X, d). Коэффициентом сжатия СИФ называют s = max{sj : i = 1,..., k}.
Для пространства (X, d) можно определить другое метрическое пространство (H(X),h), называемое пространством фракталов.
Пусть H(X) множество непустых компактных подмножеств X. Определим на нем метрику Хаусдорфа h следующим образом. Пусть B(x,r) замкнутый шар, радиуса r с центром в точке х. Для произвольного множества A G X дилатацией6 Ar радиуса r множества A называется UxeA B(x,r). Таким образом, дилатация множества A это добавление к A всех точек, лежащих на расстоянии ^ r от его границы.
Пусть A, B непустые компактные подмножества из X. Тогда расстояние(метрика) Хаусдорфа определяется как (рис. 5)
h(A,B) = min{r 0|A с Br; B c Ar}.
Таким образом, это минимальное из двух чисел: первое из них получается расширением множества A, до тех пор, пока его образ не поглотит B, второе дилатацией B, пока она не поглотит A
5Такую СИФ иногда называют гиперболической.
6Т.е. расширением.
7Другое определение дано в глоссарии.
Можно показать, что если (X, d) полное метрическое пространство, то (H(X), h) также является полным метрическим пространством. Определим преобразование T : H(X) ^ H(X) как
к
T(В) = и fi(B),ув е н(X),
i= 1
где T(В) = {T(x)|x е В} оператор Хатчинсона.
Пусть В е H и Ton композиция8 порядка n оператора T:
To0(B) = В, To(j+1)(B) = Toj(T(В)).
Последовательность множеств, полученная в результате итерирования T(В), т.е.
{В^ (B),T o2(b),T ^(В),...^ оп(В),...},
называется орбитой В для (H(X),T). Пару (H(X),T) можно рассматривать как детерминированную дискретную динамическую систему с пространством состояний H(X) и преобразованием T.
Согласно теореме Банаха о неподвижной точке, действие сжимающего преобразования T на произвольную начальную точку В0 е H в пространстве (H(X), h) приводит к последовательности точек В0,В1 = T(В0),В2 = T(В1) = To2^0),..., которая сходится к некоторой точке A е H. Она является единственным решением уравнения T(A) = A. Очевидно, что
lim Ton (В) = A.
n ^
Неподвижная точка A называется аттрактором СИФ или фракталом.
При практическом использовании СИФ для построения фракталов оператор Хатчинсона применяют только к граничным точкам компакта.
Пример 1. Пусть X = [0,1], f1 = 1/3x, f2 = 1/3x + 2/3. Пусть
T = f1 U f2. Последовательность итераций T(X) при n те
T([0,1]) = {[0,1/3], [2/3,1]},
To2 = {[0,1/9], [2/9,1/3], [2/3,7/9], [8/9,1]},...
очевидно приводит к канторову множеству: F = П Ton[0,1]. Пример 2. Пусть X € R2. Определим СИФ как
Хі
Х2 = 1/2
0 0
1/2 Хі
Х2 + О О Хі
Х2 ) = 1/2
0 0
1/2 Хі
Х2 + 1/2 ' 0 Хі
Х2 ) = 1/2
0 0
1/2 Хі
Х2 + 1/2 ' 1/2
аффинные преобразования сжатия B с коэффициентом 0.5. Преобразование /з сдвигает образ B вправо на 1/2, f2 вверх на эту же величину и / оставляет его на месте. Таким образом, для каждого n Ton(B) репродуцирует сжатие и сдвиги.
Заметим, что любое аффинное преобразование в R2 кодируется всего шестью коэффициентами, поэтому СИФ реализует фрактальное сжатие изображения ковра. Множество
T(B) : fi(B) U f2(B) U f3(B) представляет собой композицию (коллаж) трех уменьшенных копий B. Нахождение коэффициентов аффинных преобразований по фрагменту коллажа называют обратной задачей в теории фракталов. В ее решении важную роль играет следующая Теорема о коллаже.
Пусть {(X, d); f1,f2 ,...,fk} гиперболические СИФ с коэффициентом сжатия s, B произвольное непустое компактное множество, принадлежащее H(X) и A аттрактор СИФ. Пусть
к
h(B\]fi(B)) = h(B,T(B)) р.
І= 1
Тогда
р
h(A,B) h(B,T(B))--.
1 s
Таким образом, для решения обратной задачи следует выбирать B, похожее на фрагмент коллажа.
Системой случайных итеративных функций (ССИФ)
{X; fi,f2,... ,fk; pi,p2,...,pk.}
называют СИФ, снабженную набором вероятностей {pi|i = 1,2,... ,k} для каждого fi, где pi 0 и pi + p2 + ... + pk = 1. Пусть а =
(a1,...,aN); ап G {1,...,k}. Тогда орбита ССИФ определяется как Xn+1 = fan (xn), где fan выбирается с вероятностью(1) pGn.
Предположим, что преобразования fi, i = 1,2,3 при построении ковра Сер-пинского выбираются с фиксированными вероятностями p1 p2 p3. Тогда, образы f1 (B) при итерациях T будут появляться в среднем чаще и, следовательно, соответствующие фрагменты в ковре окажутся более черными на каждом масштабе. При этом условие нормировки вероятностей при переходе к второй итерации индуцирует новые вероятности:
(p1) ^ (p1 p1, p1 p2 ,p1 p3)
(p2) ^ (p2p1, p2p2 ,p2p3)
(p3) ^ (p3p1,p3p2 ,p3p3)
Эта цепочка продолжается с ростом номера итерации и мы получим ковер Серпинского в черно-серо-белых тонах, причем интенсивность окраски (мера) приобретает скейлинговые свойства. На другом языке такую картину называют мультифрактальной мерой.
Заметим, что кроме ССИФ существуют их разновидности рандомизированные СИФ. Это обычные итеративные функции, коэффициенты которых выбираются случайно на каждом шаге итерации из некоторого множества.
Пример аттрактора такой СИФ приведен на рис. 7.
Примечания
1. Рассмотрим некоторое измеримое множество B, в которое может заходить орбита ССИФ. Эргодическая теорема Элтона утверждает, что для каждой последовательности символов {тп} частота, с которой орбита {xn} посещает B, равна мере этого множества MF (B).
Mf(b), b c b(x),
Й{жп € B : 1 n N}
lim --
NN
где И заменяет слово количество. Другими словами, последовательность точек орбиты ССИФ x п = о f„n-1 о ... о fai (xo) сходится к глобальному аттрактору в смысле расстояния Хаусдорфа для почти каждой точки x0 € X и для любого набора вероятностей.
Путеводитель по литературе. Оригинальная работа Хатчинсона [21] трудна для первого чтения, однако существует ее упрощенный вариант [22].
Наиболее полное изложение СИФ и ССИФ дано в книге Барнсли [2] и в недавно переведенной книге Кроновера [23]. Хорошие введения в теорию детерминированных и случайных СИФ можно найти на Web-страничках, см., например, [24].
Основные идеи мультифрактально-го формализма можно найти в [20,22].
Динамические системы и странные аттракторы
Поэтому, если тебе сначала все покажется пустым бредом, знай, что причиной твоя слабость!
Николай Кузанский Берилл
Дискретная динамическая система задается отображением(1)
xn+1 f (xn),x ? R -
Пространство, в котором работает отображение, обычно называют фазовым. Траектория такой системы получается последовательным применением оператора f:
xi = f (xo); Х2 = f (xi) = f (f (xo)) = fo2(xo) - ..
Для некоторых систем траектории образуют множества, весьма экзотического вида. Одно из таких множеств приведено на рис. 8. Оно образовано итерациями системы:
x„+i = Уп - sign(xn) |x„|1/2 I Уп+1 = 0.4 - xn

Как и в случае СИФ, неподвижные точки xf отображения f определяются решением уравнения: f (xf) = xf. Неподвижные точки могут быть устойчивыми, если к ним сходиться последовательность точек fon(x0), n ^ те, и неустойчивыми, в противном случае.
Легко понять, в каких случаях возникает устойчивость. Рассмотрим возмущенную неподвижную точку x = xf + Sx, которую можно получить с помощью малого возмущения отображения f:
x„+i = xf + Sxn+1 = f(xf + Sx„) ~ f(xf) + Sxnf'(xf).
Поскольку Sxn+1 = f'(xf )Sxn, понятно, что |Sxn| будет увеличиваться, если |f'(xf )| 1. Таким образом, производная |f '| играет роль локального коэффициента сжатия или расширения для нелинейного (в общем случае) отображения f. Очевидно, что устойчивой неподвижной точке соответствует сжатие: |f '(xf )| 1. Для многомерного случая надо вы-
дхг
числять производные по всем координатам, т. е. якобиан J = det | |
отображения f в точке xf = (xj,x2j,...,x1^). В этом случае условие
устойчивости J 1 соответствует сжатию в J раз объема исходного параллелепипеда, натянутого на координатные оси, которое происходит под действием отображения f.
Разновидностью неподвижных точек являются периодические точки отображения f: говорят, что точка x периодическая с периодом р, если существует такое минимальное число р, что f p(x) = x. Все эти объекты инвариантны относительно действия отображения или его итераций. Это весьма напоминает фракталы предельные образы СИФ, которые остаются инвариантными под действием оператора Хатчинсона.
Для того, чтобы сделать эту аналогии более точной, введем некоторые дополнительные определения.
Точка у называется ш-предельной точкой для точки х, если fn(x) ^ У, n ^ те.
Иными словами, предельная точка это конец траектории, которая начинается в x. Все ш-предельные точки образуют ш-предельное множество. Следующим важным понятием является обобщение идеи инвариантности неподвижных и периодических точек относительно действия f на множества.
А именно, множество B G Rn называют инвариантным, если для всех n ^ 0, fn(B) = B. Окрестностью множества B называют открытое множество U, которое содержит B и все его предельные и граничные точки. Можно представить себе это множество как шар без границ, внутри которого находится все B и все точки, которые служат пределами сходящихся последовательностей точек из B. Наконец, расстоянием между точкой x и множеством B называют наименьшее из всех расстояний, когда точка у пробегает по всему B, т. е. 1(x,B) = infуев ||x - y||.
Замкнутое инвариантное множество A С X называется притягивающим множеством, если для него существует окрестность U такая, что Vx G U fn(x) ^ A при n ^ те. Наибольшее U, которое обладает таким свойством, называется бассейном притяжения для A. Иногда свойство притяжения формулируют на языке асимптотической устойчивости. Множество A называют устойчивым по Ляпунову если начальное расстояние 1(x, A) S между любой точкой и множеством со временем становится меньше любого заданного числа е, т. е. 1(fn(x),A) е. Если, кроме того, е ^ 0 при n ^ те множество называют асимптотически устойчивым.
Именно таким и является притягивающее множество.
Наиболее важное понятие аттрактор основано на выделении минимальной структуры притягивающего множества. Аттрактором A называют притягивающее множество, содержащее точку х, для которой ш(х) = A. Иными словами, аттрактор содержит целиком всю траекторию f on(x). Иногда говорят, что A содержит всюду плотную траекторию х, понимая под этим, что в окрестности любой точки траектории на аттракторе, можно найти другую точку этой же траектории.
Кроме того, если наугад выбранная точка аттрактора оказалась пустой, не надо отчаиваться: в ее локальной окрестности обязательно найдется точка траектории. Часто на аттракторе можно ввести меру, т. е. некоторое число, аналогичное объему в евклидовой геометрии . Это число в ряде интересных случаев можно оценить как относительную долю времени, которое проводит траектория в некотором компактном подмножестве аттрактора.
Тогда динамическая неразложимость аттрактора означает существование на нем инвариантной меры(2), которая не может быть представлена как взвешенное среднее нескольких ненулевых инвариантных мер.
Аттракторы возникают, как правило, для диссипативных динамических систем. В том случае, если фазовым пространством является R2, такие аттракторы имеют тривиальную структуру: это неподвижные точки и предельные циклы.
Однако, в Rn, n ^ 3, диссипативные системы могут иметь экзотические аттракторы с фрактальной структурой.
Рассмотрим в качестве примера так называемый аттрактор Хенона. Исходная динамическая диссипативная система описывается нелинейными дифференциальными уравнениями в R4.
Для упрощения исследования эволюцию траекторий многомерных систем часто отображают на так называемое сечение Пуанкаре в фазовом пространстве. Этот прием заключается в следующем.
Рассмотрим плоскость, ортогональную фазовым траекториям. Каждый момент прохождения орбиты через плоскость будем отмечать парой координат (xn,yn) той точки, в которой траектория протыкает плоскость. Тогда динамика исходной системы редуцируется
к дискретным преобразованиям (xn,yn) ^ (xn+1,yn+1) точек плоскости. В частности, преобразование Хенона в Д2 задается оператором
Т . xi+1 yi + 1 axi, yi+i bxi.
Этот оператор представляет собой композицию трех преобразований:
1. Т' : x' = x, y' = у + 1 ax2
2. Т'' : x'' = bx', у = y'
3. Т''' : x''' = y'', у' = x
Первое преобразование складывает фигуру и сохраняет площадь, второе сжимает фигуру относительно оси x и уменьшает площадь, умножая ее на постоянный множитель b 1, третье поворачивает и сохраняет площадь, но меняет ее знак. Якобиан отображения равен
d(xi+i,yi+i) = ь d(xi,yi) '
Значение |b| 1 соответствует сжатию. На рис.
9 приведен аттрактор преобразования Хенона для значений параметров a = 1.4; b = 0.3. Известно, что бокс-размерность этого аттрактора равна 1.26, так что это фрактал.
Фрактальные аттракторы связаны с так называемыми сценариями динамического хаоса(2). Хаотические системы описываются полностью детерминированными уравнениями, однако прогноз их решений не может быть продолжен дальше некоторого ограниченного интервала времени. Это эффект так называемой существенной зависимости от начальных условий, которые всегда задаются с конечной точностью.
Рассмотрим простой пример динамической системы , заданной на интервале I = [0,1] отображением: xn+1 = 2xn, mod 1. Динамика системы сводится просто к удвоению координаты точки и отбрасыванию единицы (это и обозначается как mod 1), если полученное значение координаты становиться больше, чем размеры фазового пространства. Выберем начальную точку из интервала I и запишем ее координату (адрес) в виде двоичного кода. Это всегда можно сделать единственным образом, если
заранее оговорить выбор способа записи для чисел, допускающих два варианта адреса. Итак, пусть например, х0 = 0,101101, где адрес записан с точностью до шестого разряда.
Последнее означает, что мы не знаем, какой из двух символов 0 или 1 стоит в следующем разряде.